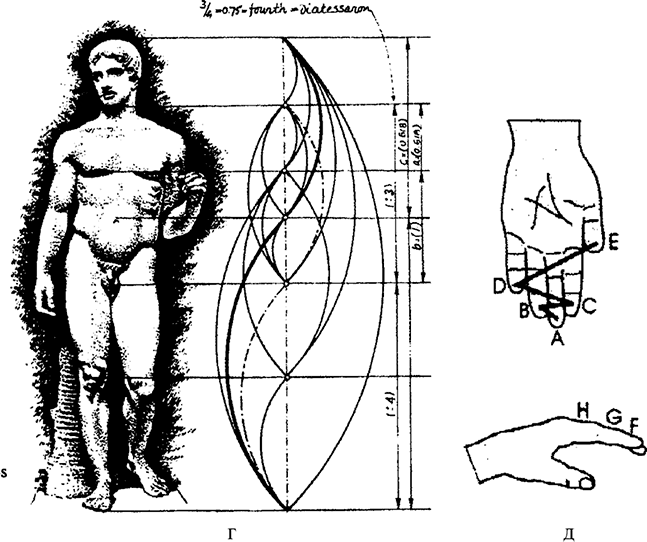
Золотое сечение пропорция в строении тела: Золотое сечение в строении тела человека

Содержание

Золотое сечение в строении тела человека

Первый пример золотого сечения в строении тела человека (рис.1) Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618. Кроме этого есть и еще несколько основных золотых пропорции нашего тела: расстояние от кончиков пальцев до запястья и от запястья до локтя равно 1:1.618

расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618
расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618
расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618
р
Рис.1 Золотое сечение в фигуре человека
ХХеси-О
асстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1. 618
расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618
расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618

Золотое сечение в чертах лица человека как критерий совершенной красоты.

В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора. К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.

На человеческом лице существуют и иные воплощения правила золотого сечения (рис.2). Приведем несколько таких соотношений:

Высота лица / ширина лица,
Центральная точка соединения губ до основания носа / длина носа.
В
Рис.2.Золотая пропорция головы человека
ХХеси-О
ысота лица / расстояние от кончика подбородка до центральной точки соединения губ
Ширина рта / ширина носа,
Ширина носа / расстояние между ноздрями,
Расстояние между зрачками / расстояние между бровями.

Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.

Рис.3. Золотая пропорция руки человека

ХХеси-О

умма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).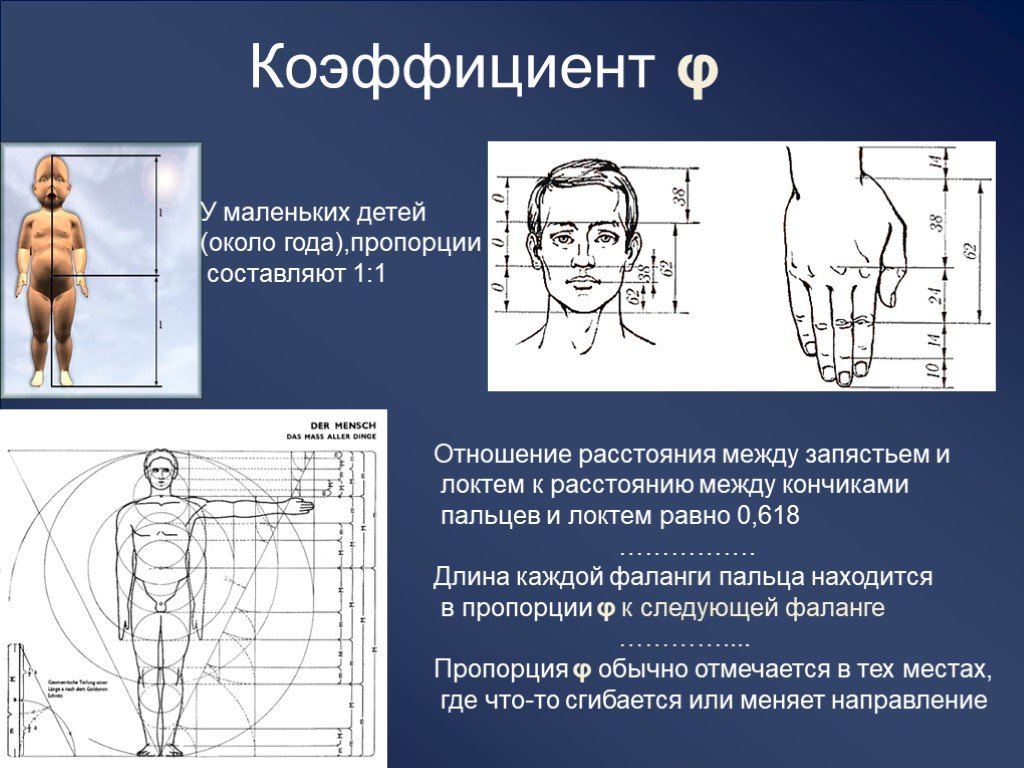 Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения. У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.

Золотое сечение: Как это работает?

Дизайн
4 мин на чтение
141090

Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.

История

Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой — Отца, а целое — Святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Природа

Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике.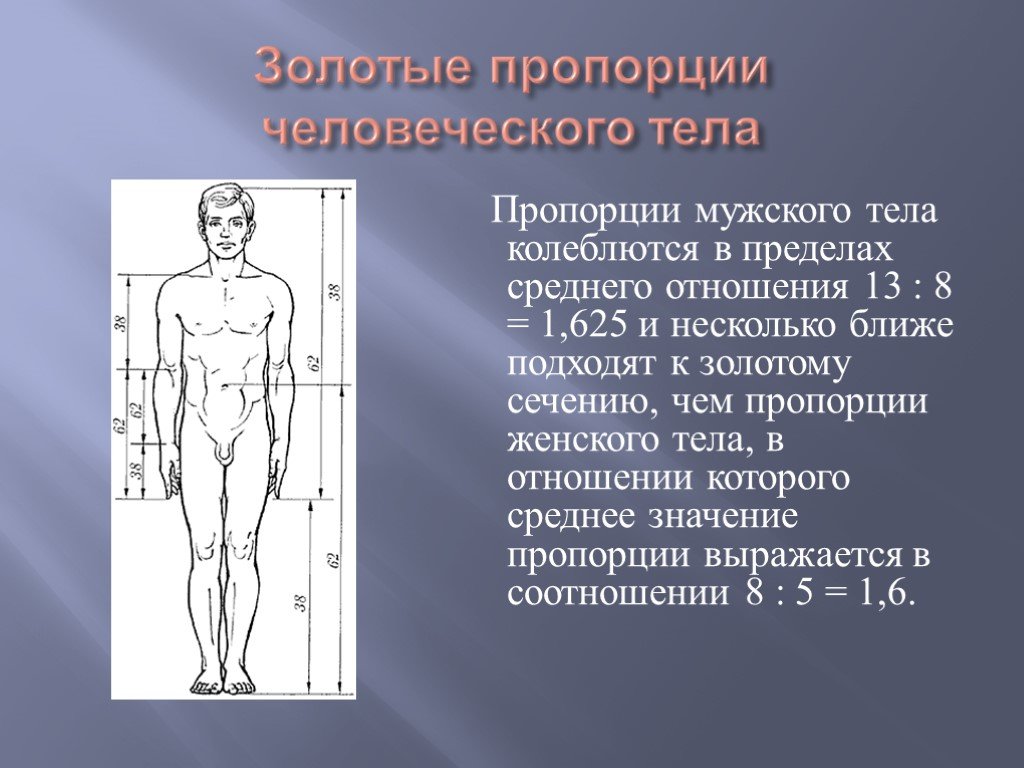 Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Человек

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек — это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.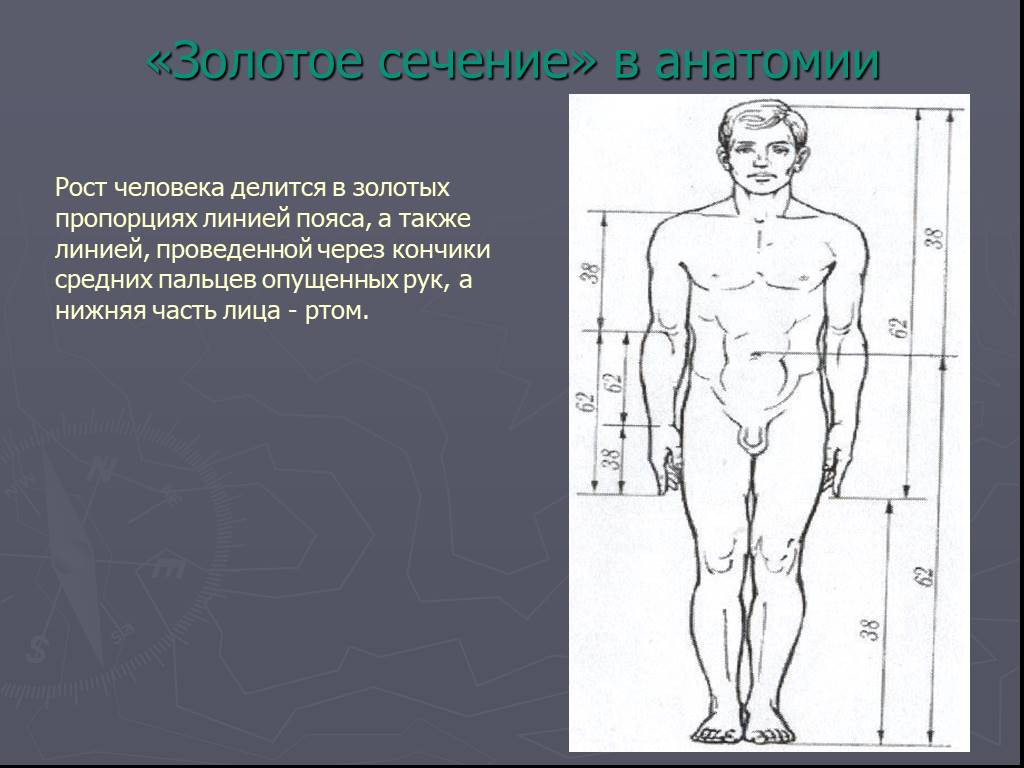

Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела — 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следовали этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.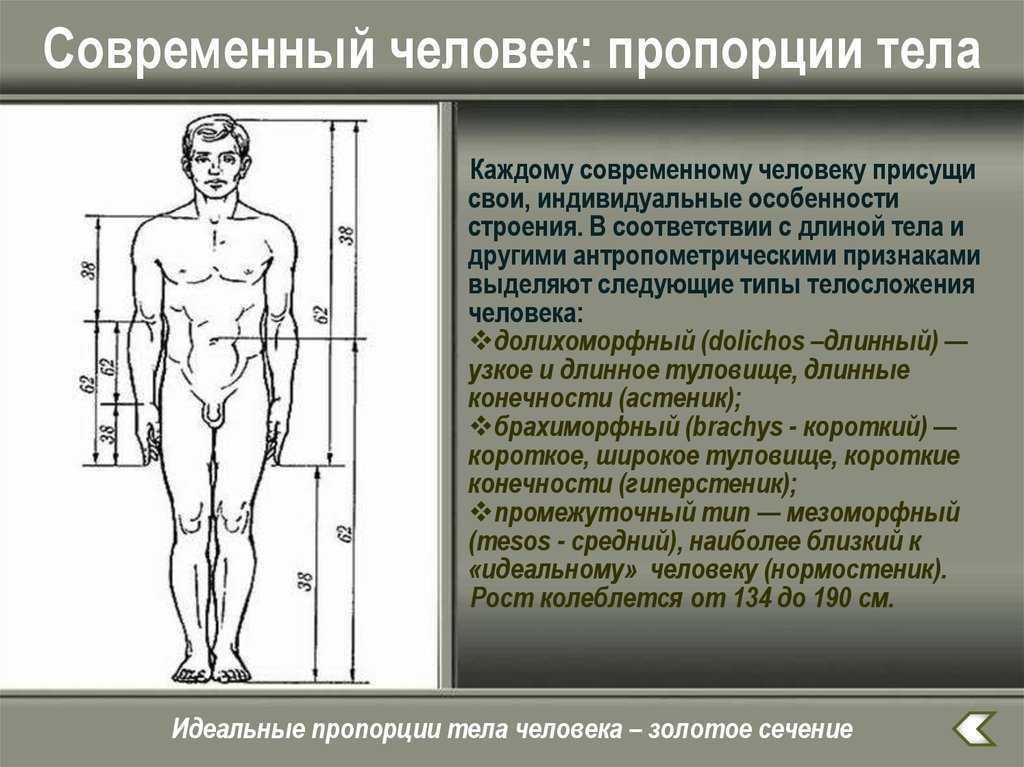

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента

Формы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) — это и есть точка золотого сечения.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух — в Одессе.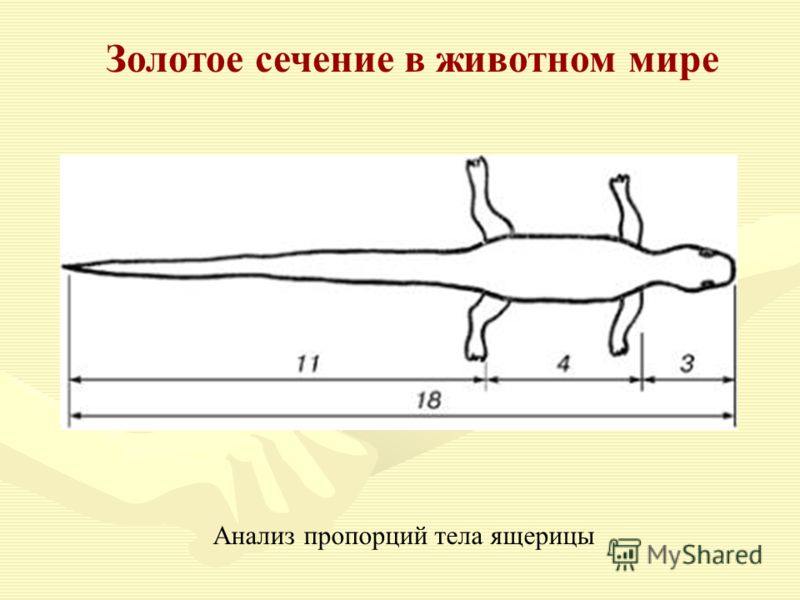 Переход на сцены в городе и есть золотая середина фильма.

Источник: Academic Painting

#дизайн
#статья

Школа искусств

Grays — И.Т. Интернет

Композиция и золотое сечение

Что такое композиция?

Композиция используется для направления взгляда по изображению и влияет на то, как зритель интерпретирует визуальную информацию.

Композиция может относиться к размерам, положениям и пространственным отношениям различных элементов в изображении.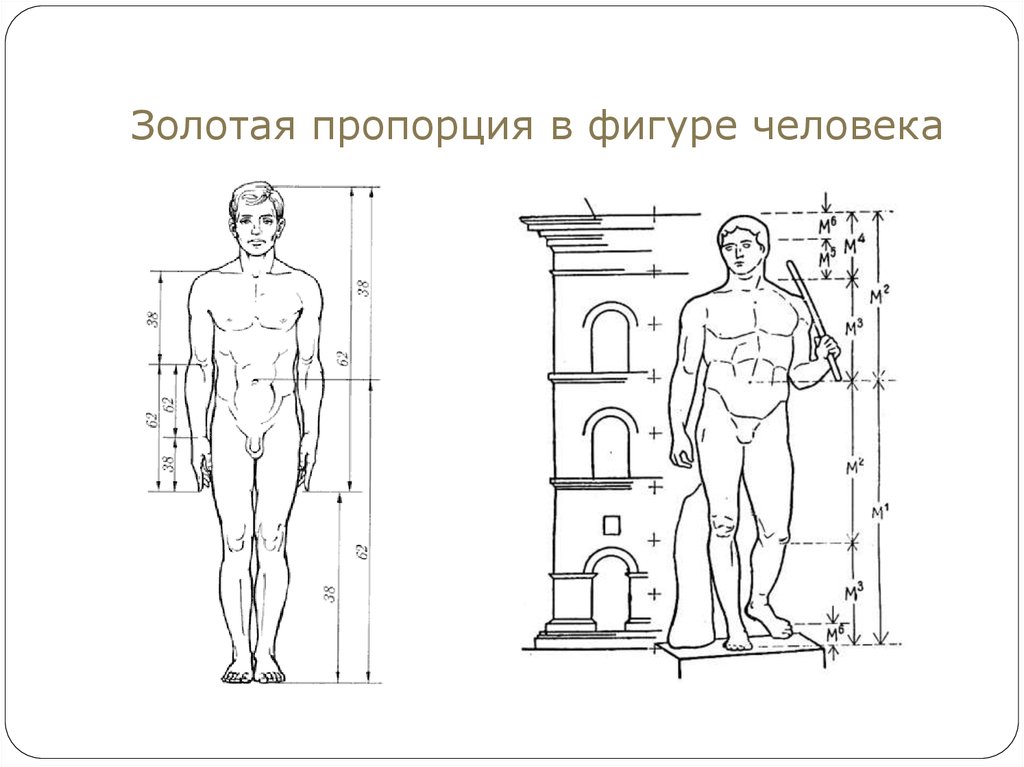
Его можно использовать как способ организации элементов на странице или экране или для создания ощущения динамического визуального напряжения.

В зависимости от расположения элементов общий эффект будет либо эстетически приятным, либо эстетически неприятным.

Какой из приведенных ниже прямоугольников кажется вам наиболее удачным?

Нажмите на изображение выше

Золотое сечение — 1:1,618 (также известное как Золотое сечение)

Большинство людей, независимо от их культурного происхождения, находят эти композиционные пропорции эстетически приятными.

В конце 19 века немецкий психолог Густав Фехнер исследовал реакцию человека на прямоугольные формы на основе золотого сечения.

Он измерил тысячи прямоугольных предметов — например, книг, газет, коробок, зданий и т.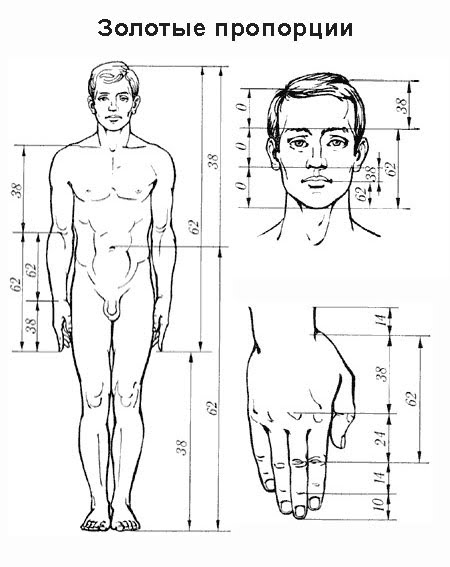 д. — и обнаружил, что большинство людей предпочитают смотреть и использовать прямоугольные предметы с пропорциями 1:1,618

Подобные эксперименты были проведены и достигли примерно таких же результатов.

Геометрия дизайна, книга графического дизайнера по имени Кимберли Элам ссылается на это.

(The Geometry of Design, Princeton Architectural Press, New York, 2001)
Нажмите здесь, чтобы увидеть, как рисуется прямоугольник золотого сечения

Божественная пропорция
Внешний вид прямоугольников, созданных с использованием Золотого сечения, основан на Божественной пропорции .
Соотношение 1 : 1,618 также известно как греческая буква Фи.
http://en.wikipedia.org/wiki/Image:Phi_uc_lc.svg
(Математическая формула Божественной пропорции: (AB разделить на AC) = (AC разделить на CB)

Похоже, что структура на основе (или приблизительно на основе) измерения божественной пропорции будут выглядеть эстетично.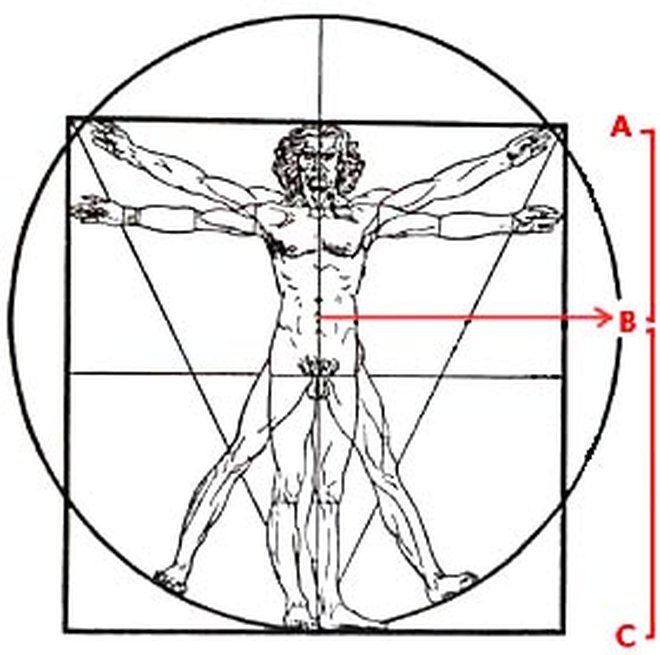

Дизайнеры могут использовать это понимание пропорций, чтобы сделать свою работу более визуально привлекательной.
Многие дизайнеры сознательно не используют Божественную Пропорцию в своей повседневной работе.
Однако может случиться так, что люди, тяготеющие к областям искусства и дизайна, интуитивно понимают эту систему пропорций и используют ее неосознанно.

Примеры золотого сечения, как оно проявляется в человеческом теле
Возможно, люди предпочитают пропорции золотого сечения и находят их использование визуально привлекательным потому, что на подсознательном уровне мы привыкли видеть эти пропорции в себе и друг друга.
• Отношение кисти к предплечью приблизительно соответствует Золотому сечению.
(Обратите внимание, что на практике соотношение может быть ниже.)

——
• Каждая кость указательного пальца руки примерно в 1,618 раза больше, чем предыдущая кость
(От кончика указательного пальца к ладони).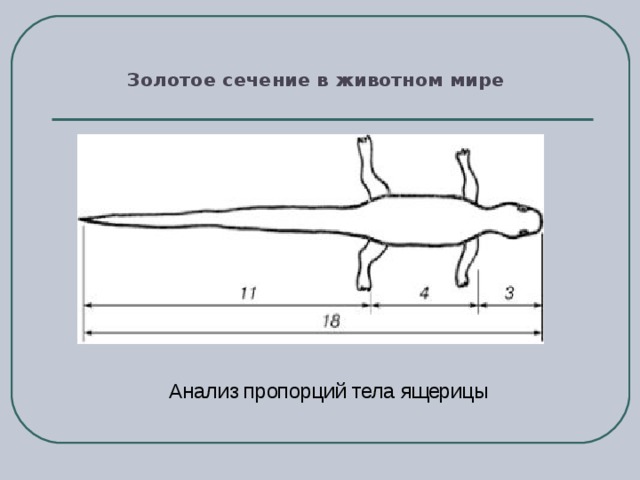 в «раскладке» наших лиц.
http://goldennumber.net/images/face-phi.png
——
• Профессор Стивен Марквардт считает, что человеческая привлекательность может быть связана с золотым сечением.
Он разработал «маски для лица» на основе математики золотого сечения и утверждает, что лица людей, которых можно назвать «привлекательными», кажутся вписывающимися в очертания, появляющиеся на масках.

http://www.beautyanalysis.com/index2_mba.htm
(Идеальное лицо > Маски)
http://www.intmath.com/Numbers/mathOfBeauty.php
Попробуйте наложение интерактивных масок Flash «game»
Последовательность Фибоначчи
Леонардо Пизанский (также известный как Фибоначчи) был итальянским математиком XII-XIII веков.

Он представил индо-арабские цифры, которые были важны для десятичной системы счисления, в Европу через публикацию своей книги Liber Abacci (что означает 9).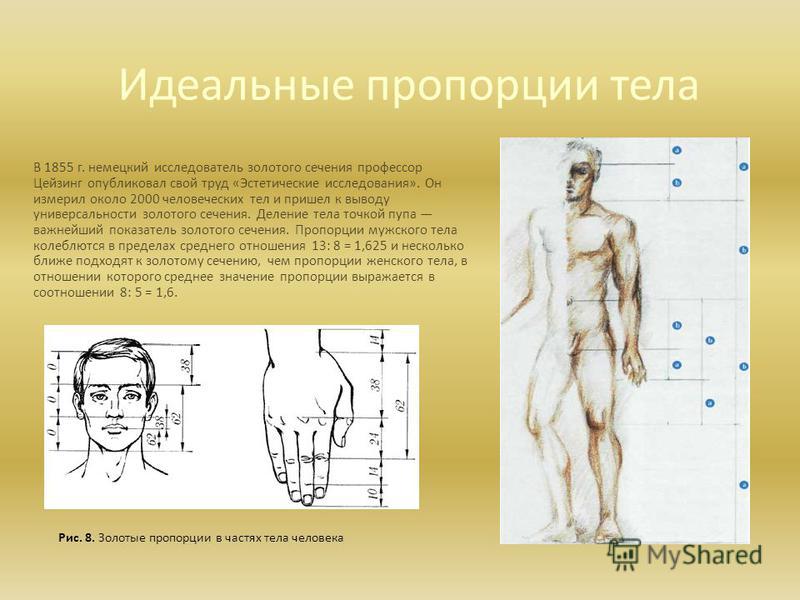 0053 Книга Чисел или Книга Расчетов. )
Последовательность Фибоначчи — это серия чисел, названная в его честь и которую он тщательно изучал.
(На самом деле он не открыл свойства чисел сам, хотя последовательность теперь названа в его честь.)
В приведенной ниже последовательности Фибоначчи каждое третье число получается путем сложения двух предыдущих чисел.
т.е.
1
1
2 (1+1)
3 (1+2)
5 (2+3)
8 (2+3)
(2+3). 13 (5+8)
21 (8+13)
34 (13+21)
etc
Говорят, что последовательность Фибоначчи связана с золотым сечением.
Начиная с числа «3», все числа в последовательности — если они делятся на предыдущее число — дают результат, равный 9.0053 приблизительно 1,618
Когда мы рисуем квадрат внутри прямоугольника золотого сечения, оставшаяся прямоугольная форма также имеет пропорции золотого сечения.
Эта оставшаяся прямоугольная форма примерно в 1,618 раза меньше, чем предыдущий прямоугольник Золотого сечения, в котором он находится.
Этот процесс можно повторять бесконечно, как показано ниже.
——
Когда мы рисуем спираль на основе прямоугольников золотого сечения, повторяющихся внутри больших прямоугольников золотого сечения,
мы обнаруживаем, что форма этой спирали напоминает формы, наблюдаемые в мире природы.
например, морская раковина.
Морские раковины вырастают примерно в 1,618 раз больше на каждой фазе своего роста. >>
http://en.wikipedia.org/wiki/Image:Fibonacci_spiral. svg

Говорят, что золотое сечение 1:1,618 встречается во многих других областях.
Древние греки считали золотое сечение эстетически привлекательным и писали об этом еще в 5 веке. Они предположили, что мы можем найти примеры Божественной Пропорции в рукотворном мире, а также в мире природы.
• Парфенон в Афинах, Греция
Структура фасада Парфенона разделена с использованием пропорций золотого сечения.
• Внешняя форма Парфенона вписывается в прямоугольник с соотношением сторон 1:1,618
• Фасад был разделен таким образом, чтобы соответствовать шаблону, появляющемуся, когда прямоугольник Золотого сечения рисуется, а затем повторяется внутри самого себя.
Другие примеры —
• http://goldennumber.net/
• http://goldennumber.net/acoustics.htm
• http://goldennumber.net/music.htm
Канон Витрувия
Маркус Витрувий Поллион (известный как Витрувий) был греческим ученым и архитектором, который работал примерно между 80 г. до н.э. и 25 г. до н.э. Он считал, что архитектурные пропорции греческих храмов должны основываться на визуально гармоничных пропорциях человеческого тела.
Художники эпохи Возрождения Леонардо да Винчи и Альбрехт Дюрер использовали Витрувий Канон в конце 15 века и в начале 16 века.
По ссылке ниже показано одно из самых известных изображений идеализированных пропорций. «Витрувианский человек» Леонардо да Винчи.
http://en.wikipedia.org/wiki/Image:Da_Vinci_Vitruve_Luc_Viatour.jpg
Он отметил ряд особенностей пропорций человеческого тела —
• Высота от ступней до макушки примерно равна длине рук в вытянутом состоянии
• Высота туловища и длина вытянутых рук равны, Таким образом, на основе этих измерений можно нарисовать квадрат, который заключает в себе все тело
• Если фигура стоит с широко расставленными ногами и вытянутыми/поднятыми вверх руками все они будут соприкасаться с точками на окружности, если их начертить используя расстояние между пупком и ступнями в качестве радиуса
• Фигуру можно разделить по золотому сечению на уровне пупка
• Если расстояние между пупком и ступнями разделить на расстояние между пупок и голова, получаем число примерно 1,618
Однако . . .
Не все, особенно математики, убежден в этой экстраполяции математических формул — особенно с подразумеваемыми «мистическими» свойствами — из явлений природы.
Как и в большинстве источников информации, утверждающих, что «красота» может быть измерено, есть противоположная информация, которая говорит, что это не может
Выписка:
http://www.lhup.edu/~dsimanek/pseudo/fibonacc.htm
http://www.umcs.maine.edu/~markov/GoldenRatio.pdf
Корень 2 прямоугольника

Корень 2 прямоугольника имеет пропорциональное соотношение размеров 1:1,41 A4, A3 и т. д.
Любой лист, сложенный пополам по самому длинному краю, имеет следующий размер A меньше или, если его сложить вдвое по самому длинному краю, это следующий размер A вверх.
Рисунок, образованный делениями на спинке и сиденье стула «Барселона» Миса ван дер Роэ 1929 года, основан на прямоугольниках Root 2. Со стороны сама конструкция опирается на 3 простых кривых. Длина основания стула такая же, как и его высота (поэтому сбоку вся конструкция может быть заключена в квадрат).
http://en.wikipedia.org/wiki/Image:Mies-Barcelona -Chair-and-Ottoman.jpg
Нажмите здесь, чтобы увидеть, как рисуется прямоугольник корня 2
(прямоугольники Root 3, Root 4, Root 5 и т. д. основаны на аналогичной структуре)

Традиционное расположение текста на печатной странице
Говорят, что ранние рукописи были расположены с использованием пропорций, аналогичных приведенному ниже примеру.
Базовая структура, на которой размещены элементы на странице, помогает странице выглядеть хорошо сбалансированной и упорядоченной.

Общая общая пропорция страницы составляет 2:3
• Измерения здесь приблизительно основаны на пропорциях золотого сечения.
Размер каждого блока текста пропорционально размеру страницы, на которой он расположен, т. е. 2:3
• Текст размещается так, чтобы он совпадал с диагональными линиями.
• Высота каждого блока текста равна ширине каждой страницы.
Глядя на страницу слева —
• Правое поле составляет примерно 1/9 ширины страницы.
• Левое поле составляет примерно 2/9 ширины страницы.
Все еще глядя на левую страницу —
Каждое поле в два раза больше ширины поля напротив.
• Ширина левого поля в два раза больше ширины правого поля, а ширина нижнего поля в два раза больше ширины верхнего поля.
• Это дает соотношение 1 : 1,5 : 2 : 3
——
Эта система пропорций названа Канон Ван де Граафа в честь человека, который ее открыл.
Щелкните здесь, чтобы увидеть, как создается двойная страница.
——
Бумага формата «A»
Хотя приведенная выше схема считается хорошо сбалансированной, сегодня мы редко видим ее в использовании.
Бумага формата «A» (например, A3/A4/A5) стала «стандартным» форматом. Любой лист, сложенный пополам по самому длинному краю, соответствует следующему размеру «А» по размеру меньше, или, если он сложен вдвое по самому длинному краю, это следующий размер «А» по размеру.
• Печатать на бумаге формата «A» экономически выгодно, так как это легко доступный и стандартизированный размер бумаги.
• Макет, использованный при создании рукописей (см. выше), оставляет большую часть страницы пустой. Это означает, что на каждой странице можно разместить меньше текста. По этой причине книга, оформленная таким образом, потребует большего количества страниц и, следовательно, будет стоить дороже.
Современные размеры бумаги «А» вместе с производственными и экономическими требованиями могут привести к результату, больше похожему на изображение ниже.

Золотое сечение также может быть применено к макету веб-страниц
Ниже приведен скриншот веб-сайта BBC. Нажмите на изображение ниже.
Было бы довольно необычно найти веб-страницу, которая была бы выложена точно с пропорциями 1:1,618.
Однако мы можем найти некоторые примеры веб-страниц, где области страниц расположены таким образом, что приблизительно соответствует пропорциям Золотого сечения, как указано выше.
Такое использование асимметрии помогает сделать макет визуально более интересным.
Компания, ссылка на которую приведена ниже, разработала инструмент компоновки, помогающий создавать веб-страницы на основе пропорций золотого сечения. http://www.atrise.com/golden-section/screenshots.php

Школа искусств
Grays — И.Т. web
Неделя 6: Композиция и золотое сечение
Вы выписали свое имя из реестра? Если нет, пожалуйста! (Спросите, если не видите.)
Что такое композиция?
Композиция используется для направления взгляда по изображению и влияет на то, как зритель интерпретирует визуальную информацию.
Композиция может относиться к размерам, положениям и пространственным отношениям различных элементов в изображении.
Его можно использовать как способ организации элементов на странице или экране или для создания ощущения динамического визуального напряжения.
В зависимости от расположения элементов общий эффект будет либо эстетически приятным, либо эстетически неприятным.
Какой из приведенных ниже прямоугольников кажется вам наиболее удачным?
Нажмите на изображение выше

Золотое сечение — 1:1,618 (также известное как Золотое сечение) Большинство людей, независимо от их культурного происхождения, находят эти композиционные пропорции эстетически приятными.

В конце 19 века немецкий психолог Густав Фехнер исследовал реакцию человека на прямоугольные формы на основе золотого сечения.
Он измерил тысячи прямоугольных предметов — например, книг, газет, коробок, зданий и т. д. — и обнаружил, что большинство людей предпочитают смотреть и использовать прямоугольные предметы с пропорциями 1:1.618
Подобные эксперименты проводились и были достигнуты примерно такие же результаты.
Геометрия дизайна, книга графического дизайнера по имени Кимберли Элам ссылается на это. >>
(The Geometry of Design, Princeton Architectural Press, New York, 2001)
Нажмите здесь, чтобы увидеть, как рисуется прямоугольник золотого сечения

Divine Proportion
Золотое сечение основано на божественной пропорции .
Соотношение 1 : 1,618 также известно как греческая буква Фи.
http://en.wikipedia.org/wiki/Image:Phi_uc_lc.svg
(Математическая формула Божественной пропорции: (AB разделить на AC) = (AC разделить на CB)

Похоже, что структура, основанная на (или приблизительно на основе) измерений Божественной Пропорции, будет выглядеть эстетично.
Дизайнеры могут использовать это понимание пропорции, чтобы сделать свою работу более визуально привлекательной.
Многие дизайнеры сознательно не используют Божественную Пропорцию в своей повседневной работе.
Однако может случиться так, что люди, тяготеющие к областям искусства и дизайна, интуитивно понимают эту систему пропорций и используют ее неосознанно.
Примеры соотношения 1:1,618 в человеческом теле
Возможно, люди предпочитают пропорции золотого сечения и находят их использование визуально привлекательным потому, что на подсознательном уровне мы привыкли видеть эти пропорции в себе и друг в друге .

• Отношение кисти к предплечью приблизительно равно Золотому сечению 1:1,618

——
• Каждая кость указательного пальца вашей руки примерно в раз больше, чем
4 1,6 предшествующая ей кость
(От кончика указательного пальца к ладони. )
http://goldennumber.net/hand.htm
——
• Пропорции Золотого Сечения также можно найти в «раскладке» наших лиц.
http://goldennumber.net/images/face-phi.png
——
• Профессор Стивен Марквардт считает, что человеческая привлекательность может быть связана с золотым сечением.
Он разработал «маски для лица» на основе математики золотого сечения и утверждает, что лица людей, которых можно назвать «привлекательными», кажутся вписывающимися в очертания, появляющиеся на масках.

http://www.beautyanalysis.com/index2_mba.htm
(Идеальное лицо > Маски)
http://www.intmath.com/Numbers/mathOfBeauty.php
Последовательность Фибоначчи
Леонардо Пизанский (также известный как Фибоначчи) был итальянским математиком 12-13 веков.

Он познакомил Европу с индийско-арабскими цифрами, которые имели большое значение для десятичной системы счета, благодаря публикации своей книги 9. 0053 Liber Abacci (что означает Книга Чисел или Книга Расчетов. )
Последовательность Фибоначчи представляет собой ряд чисел, названных в его честь и которые он тщательно изучал.
(На самом деле он не открыл свойства чисел сам, хотя последовательность теперь названа в его честь.)
В приведенной ниже последовательности Фибоначчи каждое третье число получается путем сложения двух предыдущих чисел.
IE
1
1
2 (1+1)
3 (1+2)
5 (1+2)
5 (2+2) 44444444444444444444444444444444444444444444444444449004. 3+5)
13 (5+8)
21 (8+13)
34 (13+21)
etc
Говорят, что последовательность Фибоначчи связана с золотым сечением.
Начиная с числа «3», все числа в последовательности — если они делятся на предыдущее число — дают результат, равный 9.0053 приблизительно 1,618
Когда мы рисуем квадрат внутри прямоугольника золотого сечения, оставшаяся прямоугольная форма также имеет пропорции золотого сечения.
Эта оставшаяся прямоугольная форма примерно в 1,618 раза меньше, чем предыдущий прямоугольник Золотого сечения, в котором он находится.
Этот процесс можно повторять бесконечно, как показано ниже.
——
Когда мы рисуем спираль на основе прямоугольников золотого сечения, повторяющихся внутри больших прямоугольников золотого сечения,
мы обнаруживаем, что форма этой спирали напоминает формы, наблюдаемые в мире природы.
например, морская раковина.
Морские раковины вырастают примерно в 1,618 раз больше на каждой фазе своего роста. >>
http://en.wikipedia.org/wiki/Image:Fibonacci_spiral. svg
Говорят, что золотое сечение 1:1,618 встречается во многих других областях.
Древние греки считали, что золотое сечение эстетично, и писали об этом еще в 5 веке. Они предположили, что мы можем найти примеры Божественной Пропорции в рукотворном мире, а также в мире природы.
• Парфенон в Афинах, Греция
Структура фасада Парфенона разделена с использованием пропорций золотого сечения.
• Внешняя форма Парфенона вписывается в прямоугольник с соотношением сторон 1:1,618
• Фасад был разделен таким образом, чтобы соответствовать шаблону, появляющемуся, когда прямоугольник Золотого сечения рисуется, а затем повторяется внутри самого себя.
Другие примеры —
• http://goldennumber.net/
• http://goldennumber.net/acoustics.htm
• http://goldennumber.net/music.htm
Золотое сечение можно также применять к формам, отличным от прямоугольников.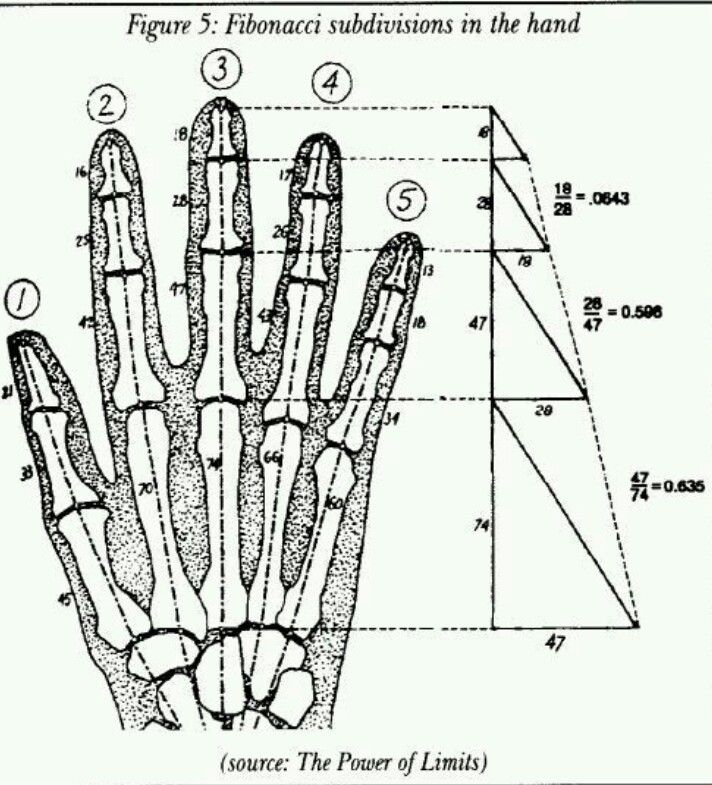
Каждый круг и квадрат ниже в 1,168 раза больше предыдущего.

——
Треугольники Золотого Сечения
Треугольник Золотого Сечения (также известный как Возвышенный Треугольник) по существу эквивалент прямоугольника Золотого сечения. Если представить несколько различных треугольных форм, большинство людей предпочтут структуру, показанную ниже.
Чтобы нарисовать возвышенный треугольник, нарисуйте пятиугольник, а затем соедините две нижние точки с верхней, как показано ниже.
——
Эллипсы золотого сечения
Эллипс золотого сечения — это эллипс, начерченный внутри прямоугольника золотого сечения. Если представить несколько различных эллиптических форм, большинство людей предпочтут структуру, показанную ниже.
——
Корень 2 Прямоугольники

Корень 2 Прямоугольник имеет пропорциональное соотношение размеров 1:1,41
Корень 2 Прямоугольники используются в качестве основы для размера стандартной бумаги «А», т.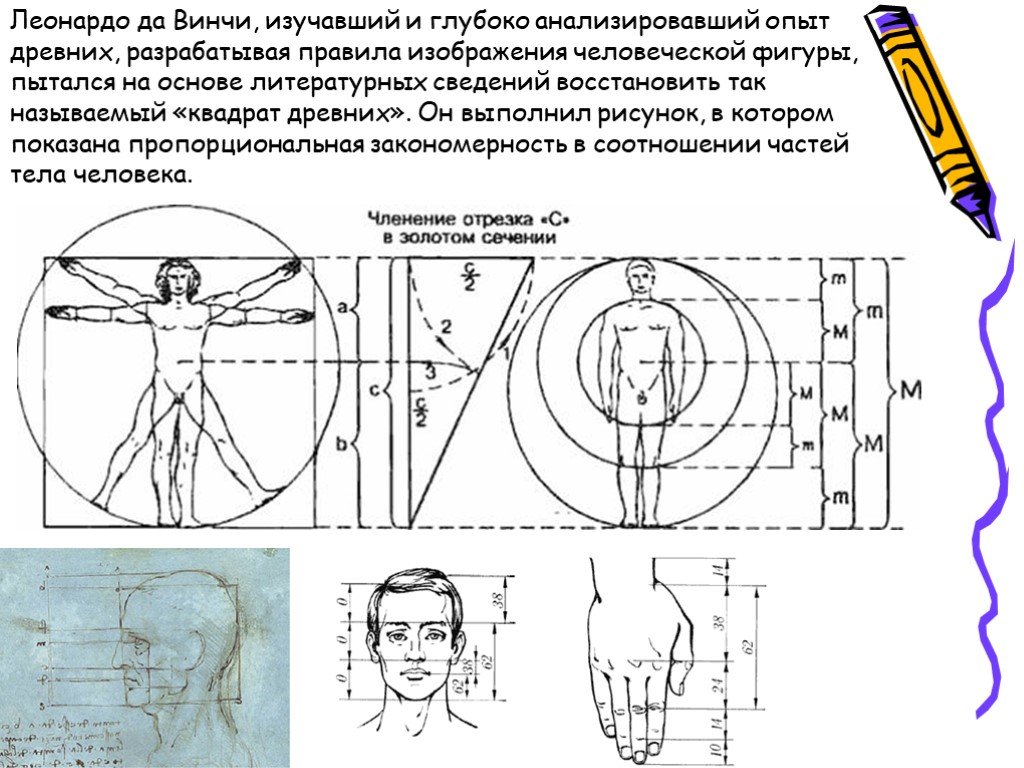 е. A5, A4, A3 и т. д.
Любой лист, сложенный пополам по самому длинному краю, имеет следующий размер A меньше или, если его сложить вдвое по самому длинному краю, это следующий размер A вверх.
Рисунок, образованный делениями на спинке и сиденье стула «Барселона» Миса ван дер Роэ 1929 года, основан на прямоугольниках Root 2. Со стороны сама конструкция опирается на 3 простых кривых. Длина основания стула такая же, как и его высота (поэтому сбоку вся конструкция может быть заключена в квадрат.)
http://en.wikipedia.org/wiki/Image:Barcelona.jpg
Щелкните здесь, чтобы увидеть, как рисуется прямоугольник с корнем 2
(прямоугольники с корнем 3, корнем 4, корнем 5 и т. д. основаны на аналогичной структуре)
Золотое сечение можно применять к макету веб-страниц
( и печатные страницы)
Ниже приведен скриншот веб-сайта BBC. Нажмите на изображение ниже.
Было бы довольно необычно найти веб-страницу, которая была бы выложена точно с пропорциями 1:1,618.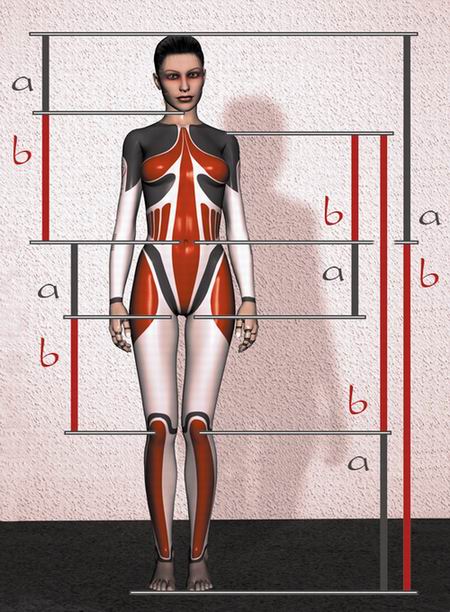
Однако мы можем найти примеры веб-страниц, где области страниц расположены таким образом, что приблизительно соответствует пропорциям золотого сечения , как указано выше.
Такое использование асимметрии помогает сделать макет визуально более интересным.
Компания, ссылка на которую приведена ниже, разработала инструмент компоновки, помогающий создавать веб-страницы на основе пропорций золотого сечения. http://www.atrise.com/golden-section/screenshots.php

На следующей неделе попробуйте найти веб-сайт, посвященный спорту, на котором в дизайне страницы применено асимметричное разделение пространства, и подумайте, как это повлияет на его общий внешний вид.
Канон Витрувия
Маркус Витрувий Поллион (известный как Витрувий) был греческим ученым и архитектором, работавшим между 80 и 25 годами до н.э. Он считал, что архитектурные пропорции греческих храмов должны основываться на визуально гармоничных пропорциях человеческого тела.
Художники эпохи Возрождения Леонардо да Винчи и Альбрехт Дюрер использовали канон Витрувия в конце 15 века и в начале 16 века.
По ссылке ниже показано одно из самых известных изображений идеализированных пропорций «Витрувианского человека», созданное Леонардо да Винчи.
http://en.wikipedia.org/wiki/Image:Da_Vinci_Vitruve_Luc_Viatour.jpg
Он отметил ряд особенностей пропорций человеческого тела —
• Высота от ступней до макушки примерно равна длине вытянутых рук
• Высота тела и длина вытянутых рук равны, поэтому на основе этих измерений можно нарисовать квадрат, охватывающий все тело
• Если фигура стоит с широко расставленными ногами и вытянутыми/поднятыми вверх руками, все они соприкоснутся с точками на окружности, если начертить ее с использованием расстояния между пупком и ступнями в качестве радиуса
• Фигуру можно разделить по золотому сечению на уровне пупка
• Если расстояние между пупком и ступнями разделить на расстояние между пупком и головой, мы получим примерно 1,618
——

.