Виды трапеций: Виды трапеций | Треугольники

24.03.2021 0 Разное

Содержание

Трапеция — что это такое, свойства и виды трапеций (равнобедренная, прямоугольная)

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы решили подробно рассказать о такой геометрической фигуре, как ТРАПЕЦИЯ.

РожицаРожица

Ее подробно изучают на уроках геометрии в 8-м классе. И эти уроки являются частью общего знакомства школьников с различными четырехугольниками.

Определение трапеции

Трапеция – геометрическая фигура, которая представляет собой четырехугольник, у которого две противоположные стороны располагаются на параллельных прямых. А две другие стороны должны, наоборот, быть не параллельными.

Определение трапеции

Определение трапеции

Вот так выглядит классическая трапеция:

ФигураФигура

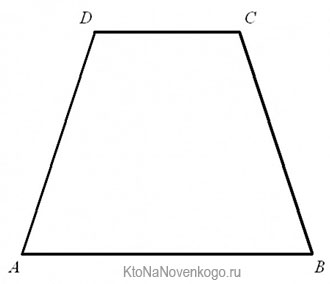
У этой фигуры стороны АВ и CD являются параллельными. А вот AD и CB – нет.

Происхождения слова

Первое упоминание об этой фигуре встречается еще в трудах известного древнегреческого математика Евклида.

В его книге «Начала» этим термином описывается абсолютно любой четырехугольник, который не является параллелограммом.

Если кто не помнит, параллелограммом называют четырехугольник, у которого противоположные стороны параллельны. Выглядит эта фигура в классическом понимании вот так:

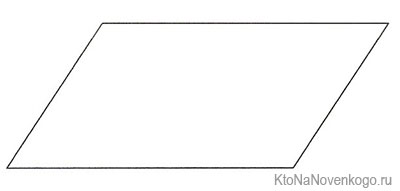
ЧетырехугольникЧетырехугольник

Интересно, что и всем известные фигуры – квадрат, прямоугольник (что это?) и ромб (это как?) – также являются частным случаем параллелограмма. Ведь действительно – у них противоположные стороны параллельны друг к другу.

ПараллельПараллель

И получается, что Евклид был в целом прав. Он просто поделил все четырехугольники на две большие категории – параллелограммы и трапеции.

Кстати, само слово ТРАПЕЦИЯ также имеет греческое происхождение. В древние времена оно звучало как «трапедзион». И в переводе это означает «обеденный стол». Поэтому слово «трапеза», которое у нас является синонимом любого приема пищи тоже родом оттуда.

Стороны трапеции

Парные стороны трапеций имеют свои названия:

  1. Основания трапеции – стороны, которые располагаются на параллельных прямых.
  2. Боковые – стороны, которые не находятся на параллельных прямых.

Закрепим это с помощью рисунка:

РисунокРисунок

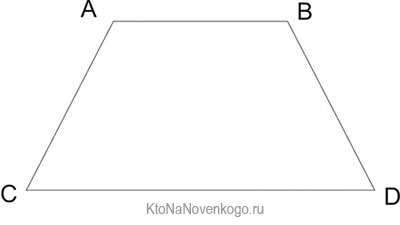
В данном случае стороны АВ и CD параллельны друг другу. А значит, именно они являются основаниями. А вот АС и BD – наоборот, явно не параллельны. И соответственно, это боковые стороны.

Кстати, расположение сторон не зависит от расположения самой фигуры. Даже вот в таких положениях

СтороныСтороны

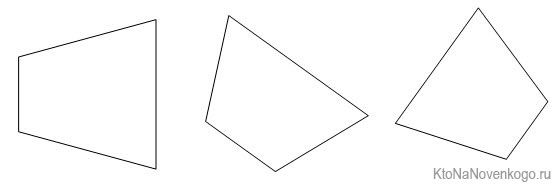
все равно параллельные стороны будут считаться основаниями, а непараллельные – боковыми.

Равнобедренная и прямоугольная трапеции

Вариант трапеции, который мы рассмотрели – это самые распространенные виды геометрической фигуры. Но есть и частные случаи:

Равнобедренная трапеция – та, у которой боковые (не параллельные) стороны равны. Ее еще называют равнобокой или равнобочной.

Выглядит она вот так:

РавнобедреннаяРавнобедренная

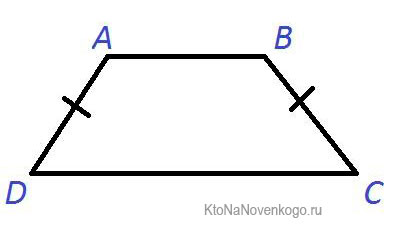
В данном примере графически показано, что стороны AD и ВС равны между собой. Об этом свидетельствуют небольшие черточки.

Прямоугольная трапеция – та, у которой одна из боковых сторон и основания образовывают прямой угол.

Выглядит она вот так:

ПрямоугольнаяПрямоугольная

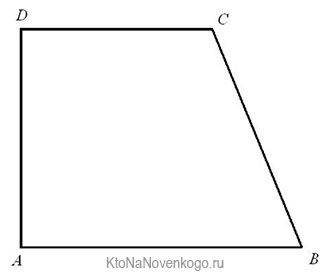
В данном примере, углы DAB и ADC являются прямыми, то есть равны 90 градусам. А соответственно, трапеция называется прямоугольной.

Тут важно заметить, что под прямым углом к основанию должна идти только одна боковая сторона. Если будут обе, то трапеция автоматически превратится в квадрат.

Свойства трапеций

С трапециями связаны несколько понятий в геометрии, которые активно используются для решения различных теорем.

Средняя линия

Средняя линия трапеции – это отрезок, который идет параллельно основаниям и соединяет середины:

Средние линииСредние линии

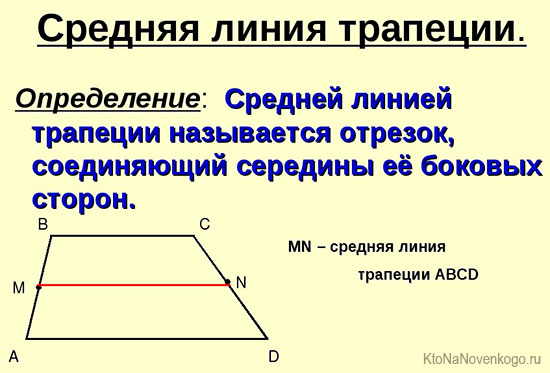
Со средней линией связана одна интересная теорема. Очень часто на уроках геометрии школьников просят определить ее длину. И сделать это весьма просто.

Длина средней линии трапеции равна половине суммы длин ее оснований.

Звучит может и несколько тяжеловато. Но на деле – это весьма просто. Так, чтобы посчитать в нашем примере длину отрезка MN, который является средней линией, надо применить формулу:

MN = (AD + ВС) / 2

И это правило распространяется на все виды трапеций.

Биссектриса углов трапеции

Биссектриса – это линия (луч), которая делит угол пополам. Так вот

Любая биссектриса, выведенная из угла трапеции, отсекает на основании отрезок, равный по длине боковой стороне.

БиссектрисаБиссектриса

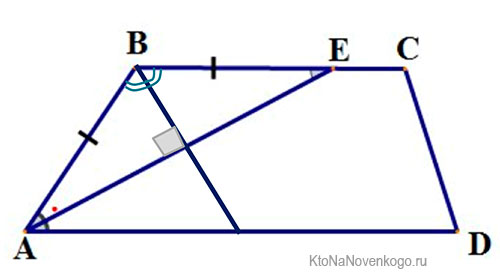
На данном рисунке отрезок АЕ является биссектрисой угла ABD. И исходя из этого, отрезки АВ и ВЕ равны между собой, о чем свидетельствуют небольшие черточки на них.
В то же время у биссектрис в трапеции есть еще одно свойство.

Две биссектрисы, выведенные из углов одной боковой стороны, пересекаются под прямым углом.

Все эти теоремы в процессе школьного обучения, ученикам еще необходимо доказывать. Ну а мы решили не приводить долгие математические и геометрические выкладки. Просто примите как данность!

Вот и все, что мы хотели рассказать вам о трапеции.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Рубрика: ЧАстые ВОпросы

Трапеция, ее свойства, формулы площади, высоты, сторон.

Трапеция, ее свойства, формулы площади, высоты, сторон.

 

 

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

 

Трапеция (понятие, определение)

Виды трапеций

Элементы трапеции: основания, боковые стороны, средняя линия и высота

Свойства трапеции

Свойства равнобедренной трапеции

Формулы трапеции

 

Трапеция (понятие, определение):

Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.

Рис. 1. Трапеция

Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

 

 

Виды трапеций:

Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.

Трапеция, виды, элементы, свойства

Рис. 2. Равнобедренная трапеция

Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.

Прямоугольная трапеция – это трапеция, имеющая

прямые углы при боковой стороне.

Трапеция, виды, элементы, свойства

Рис. 3. Прямоугольная трапеция

 

Элементы трапеции: основания, боковые стороны, средняя линия и высота:

Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.

Трапеция, виды, элементы, свойства

Рис. 4. Трапеция 

AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.

AD – большее основание трапеции, BC – меньшее основание трапеции.

Отрезок, соединяющий середины боковых сторон трапеции, называется

средняя линия.

Трапеция, виды, элементы, свойства

Рис. 5. Трапеция и срединная линия

Расстояние между основаниями трапеции называется высотой трапеции.

Трапеция, виды, элементы, свойства

Рис. 6. Трапеция

Высота трапеции (h) определяется формулой:

Трапеция, виды, элементы, свойства

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

 

Свойства трапеции:

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Трапеция, виды, элементы, свойства

Рис. 7. Трапеция и срединная линия

MN || BC, MN || AD,

l = (a + b) / 2 

2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии. 

Трапеция, виды, элементы, свойства

Рис. 8. Трапеция

MN = (b – a) / 2 

3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .

Сумма углов, прилежащих к боковой стороне трапеции, равна  180° . 

Рис. 9. Трапеция 

4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

Рис. 9. Трапеция

5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

 Рис. 10. Трапеция

AB = BK

6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Рис. 11. Трапеция

∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2 

7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.

Рис. 12. Трапеция

AB + CD = AD + BC 

В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

Рис. 13. Трапеция 

Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).

Рис. 14. Трапеция

MN = (AB + CD) / 2,

MN = (AD + BC) / 2

8. Диагонали трапеции делят ее на 4 треугольника.

Два из них, прилежащие к основаниям, подобны.

Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.

Рис. 15. Трапеция

Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции.  k = AD / BC. Отношение площадей этих подобных треугольников есть k2.

Треугольники ABO и CDO имеют одинаковую площадь.

9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.

Рис. 16. Трапеция

BC : AD = OC : AO = OB : DO

10. Диагонали трапеции d1и d2 связаны со сторонами соотношением:

d12 + d2

2 = 2ab + c 2 + d 2    

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.

Рис. 17. Трапеция

AK = KB, AM = MC, BN = ND, CL = LD,

KL – средняя линия

Рис. 17. Трапеция

AK = KB, AM = MC, BN = ND, CL = LD,

KL – средняя линия, UV – отрезок, который соединяет основания трапеции

12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:

где b – большее основание трапеции, a – меньшее основание трапеции, S1 и S2 – площади образованных трапеций, в результате разделения средней линией.

Трапеция, виды, элементы, свойства

Рис. 18. Трапеция

S1 – площадь трапеции MBCN,

S2 – площадь трапеции AMND

 

Свойства равнобедренной трапеции:

1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.

2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.

3. Углы при любом основании равнобедренной трапеции равны.

4. Сумма противоположных углов равнобедренной трапеции равна 180°.

5. Длины диагоналей равнобедренной трапеции равны.

6. Вокруг равнобедренной трапеции можно описать окружность.

7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.

 

Формулы трапеции:

Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d1 и d2 – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.

 

Формулы для определения сторон трапеции:

Через среднюю линию и одно из оснований трапеции:

a = 2m – b

b = 2m – a

Через высоту и углы при нижнем основании трапеции:

a = b + h · (ctg α + ctg β)

b = a – h · (ctg α + ctg β)

Через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a – c·cos α – d·cos β

Через высоту и углы при нижнем основании трапеции:

 

Формулы для определения средней линии трапеции:

Через длины оснований трапеции:

Через площадь и высоту трапеции:

 

Формулы для определения высоты трапеции:

Через сторону и прилегающий угол при нижнем основании трапеции:

h = c·sin α = d·sin β

Через диагонали трапеции и углы между ними:

Через диагонали трапеции, углы между ними и среднюю линию трапеции:

Через площадь и длины оснований трапеции:

Через площадь и длину средней линии трапеции:

 

Формула для определения периметра трапеции:

P = a + b + c + d

 

Формулы для определения площади трапеции:

Через основания и высоту трапеции:

Через среднюю линию и высоту трапеции:

S = m · h

Через диагонали трапеции и угол между ними:

Через все стороны трапеции:

С помощью формулы Герона для трапеции:

 

Как называется объемная трапеция?

Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.

В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.

 

Квадрат

Овал

Полукруг

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Трапеция

Тупой угол

Шестиугольник

 

Примечание: © Фото https://www.pexels.com, https://pixabay.com

 

Найти что-нибудь еще?

Похожие записи:

карта сайта

 

Коэффициент востребованности 279

Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

Трапеция,  у которой есть  прямые углы при боковой стороне, называется прямоугольной.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

 

Свойства трапеции

 

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

 

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

 

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

 

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная  окружность

 

Если в трапецию вписана окружность с радиусом   и она делит боковую сторону точкой касания на два отрезка —  и ,  то

 

Площадь

 

или где   – средняя линия

Смотрите хорошую подборку  задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Смотрите также площадь трапеции.

Трапеция

\[{\Large{\text{Произвольная трапеция}}}\]

Определения

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.

 

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.

 

Теоремы: свойства трапеции

 

1) Сумма углов при боковой стороне равна \(180^\circ\).

 

2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.


 

Доказательство

1) Т.к. \(AD\parallel BC\), то углы \(\angle BAD\) и \(\angle ABC\) – односторонние при этих прямых и секущей \(AB\), следовательно, \(\angle BAD +\angle ABC=180^\circ\).

 

2) Т.к. \(AD\parallel BC\) и \(BD\) – секущая, то \(\angle DBC=\angle BDA\) как накрест лежащие.
Также \(\angle BOC=\angle AOD\) как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\).

Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\). Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\). Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle COD}\]

 

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

 

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.


 

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

 

1) Докажем параллельность.


 

Проведем через точку \(M\) прямую \(MN’\parallel AD\) (\(N’\in CD\)). Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.

 

2) Докажем формулу.

 

Проведем \(BB’\perp AD, CC’\perp AD\). Пусть \(BB’\cap MN=M’, CC’\cap MN=N’\).


 

Тогда по теореме Фалеса \(M’\) и \(N’\) — середины отрезков \(BB’\) и \(CC’\) соответственно. Значит, \(MM’\) – средняя линия \(\triangle ABB’\), \(NN’\) — средняя линия \(\triangle DCC’\). Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]

Т.к. \(MN\parallel AD\parallel BC\) и \(BB’, CC’\perp AD\), то \(B’M’N’C’\) и \(BM’N’C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B’M’=M’B\). Значит, \(B’M’N’C’\) и \(BM’N’C\) – равные прямоугольники, следовательно, \(M’N’=B’C’=BC\).

 

Таким образом:

\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.


 

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

 

1) Докажем, что точки \(P\), \(N\) и \(M\) лежат на одной прямой.


 

Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\)). Пусть она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).

 

Рассмотрим \(\triangle BPN\) и \(\triangle APM\). Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]

Рассмотрим \(\triangle CPN\) и \(\triangle DPM\). Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]

Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\). Но \(BN=NC\), следовательно, \(AM=DM\).

 

2) Докажем, что точки \(N, O, M\) лежат на одной прямой.


 

Пусть \(N\) – середина \(BC\), \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\), она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).

 

\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]

Аналогично \(\triangle CON\sim \triangle AOM\). Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\). Но \(BN=CN\), следовательно, \(AM=MD\).

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

 

Трапеция называется равнобедренной, если ее боковые стороны равны.

 

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

 

2) Диагонали равнобедренной трапеции равны.

 

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

 

Доказательство

1) Рассмотрим равнобедренную трапецию \(ABCD\).

Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\), то \(BM\parallel CN\); \(AD\parallel BC\), тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\).

 

Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\). Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\), то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\).

 

2)

 

Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку \(\triangle ABD=\triangle ACD\). Следовательно, \(AC=BD\).

 

3) Т.к. \(\triangle ABD=\triangle ACD\), то \(\angle BDA=\angle CAD\). Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.

 

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

 

2) Если у трапеции диагонали равны, то она равнобедренная.

 

Доказательство

Рассмотрим трапецию \(ABCD\), такую что \(\angle A = \angle D\).


 

Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\), то треугольник \(AED\) равнобедренный и \(AE = ED\). Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\). Аналогично равны углы \(2\) и \(4\), но \(\angle 1 = \angle 2\), тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\), следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\).

 

В итоге \(AB = AE — BE = DE — CE = CD\), то есть \(AB = CD\), что и требовалось доказать.

 

2) Пусть \(AC=BD\). Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).


 

Т.к. \(AC=BD\), то \(x+kx=y+ky \Rightarrow x=y\). Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\).

 

Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\), чтд.

 

Определение трапеции. Виды трапеции. Свойства равнобедренной трапеции.

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Трапеция –четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны

Виды трапеции: равнобедренная и прямоугольная

Первое свойство равнобедренной трапеции – у равнобедренной трапеции боковые стороны равны

Второе свойство равнобедренной трапеции – у равнобедренно трапеции углы при основании равны

Определение прямоугольника. Свойство прямоугольника. Признак прямоугольника.

Прямоугольник –параллелограмм, у которого все углы прямые

Свойство прямоугольника – диагонали прямоугольника равны

Признак прямоугольника – если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник

Определение ромба. Свойство ромба.

Ромб –параллелограмм, у которого все стороны равны

Свойство ромба – диагонали ромба взаимно перпендикулярны и делят его углы пополам

Определение квадрата. Свойства квадрата.

Квадрат –прямоугольник, у которого все стороны равны

Первое свойство квадрата – все углы квадрата прямые

Второе свойство квадрата – диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам

Понятие площади многоугольника. Единица измерения площадей. Свойства площадей. Площадь квадрата.

 

Площадь многоугольника –это величина той части плоскости, которую занимает многоугольник

Единицы измерения площадей: квадратный сантиметр (см2), квадратный метр (м2), квадратный миллиметр (мм2) и т. д.

Первое свойство площади – равные многоугольники имеют равные площади

Второе свойство площади – если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

Площадь квадрата – площадь квадрата равна квадрату его стороны (S=a2)

 

Определение высоты параллелограмма. Площадь параллелограмма.

Высота параллелограмма –перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание

Площадь параллелограмма –

произведение основания на высоту

 

произведение сторон на синус угла между ними

 

 

полупроизведение диагоналей на синус угла между ними

Определение высоты трапеции. Площадь трапеции.

Высота трапеции –перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание. Площадь трапеции –площадь трапеции равна произведению полусуммы её оснований на высоту S= h

 

 

произведение средней линии на высоту

полупроизведение диагоналей на синус угла между ними

Площадь ромба (через диагонали). Площадь прямоугольника.

Площадь ромба –площадь ромба равна половине произведений его диагоналей

 

Площадь прямоугольника – площадь прямоугольника равна произведению его смежных сторон S=ab

Теорема Пифагора и обратная ей.

Теорема Пифагора –в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

c2 = a2 + b2

Теорема, обратная теореме Пифагора – если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный

Площадь прямоугольного треугольника. Теорема об отношениях площадей треугольников: с равными высотами; имеющих по равному углу.

Площадь прямоугольного треугольника –площадь прямоугольного треугольника равна половине произведения его катетов

Теорема об отношениях площадей треугольников имеющих по равному углу –если угол одного треугольника равен углу другого, то площади треугольников относятся как произведение сторон, заключающих равные углы

Теорема об отношениях площадей треугольников с равными высотами –если площади двух треугольников равны, то их площади относятся как основания

Определение подобных треугольников. Теоремы об отношениях периметров и площадей подобных треугольников.

Подобные треугольники –два треугольника, углы которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого

Теорема об отношении площади подобных треугольников – отношение площадей подобных треугольников равно квадрату коэффициента подобия

 




Трапеция

Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара противолежащих сторон параллельна.

Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон трапеции.

Элементы трапеции

  • Параллельные стороны называются основаниями трапеции.
  • Две другие стороны называются боковыми сторонами.
  • Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
  • Расстояние между основаниями называется высотой трапеции.

Виды трапеций

  • Трапеция, у которой боковые стороны равны, называется равнобедренной.
  • Трапеция, у которой один из углов «прямой», называется прямоугольной.

Основные свойства трапеции

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

\[ AB + CD = BC + AD \]

Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

\[ AK = KB, AM = MC, BN = ND, CL = LD \]

Средняя линия трапеции параллельна основаниям и равна их полусумме:

\[ m = \dfrac{a + b}{2} \]

Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

\[ \dfrac{BC}{AD} = \dfrac{OC}{AO} = \dfrac{OB}{DO} \]

Диагонали трапеции d1 и d2 связаны со сторонами соотношением:

\[ d_1^2 + d_2^2 = 2ab + c^2 + d^2 \]

Формулы длин сторон трапеции

Формула длины оснований трапеции через среднюю линию и другую основу:

\[ a = 2m — b , b = 2m — a \]

Формулы длины основ трапеции через высоту и углы при нижнем основании:

\[ a = b + h · (ctg \alpha + ctg \beta) , b = a — h · (ctg \alpha + ctg \beta)\]

Формулы длины основ трапеции через боковые стороны и углы при нижнем основании:

\[ a = b + c·cos \alpha + d·cos \beta, b = a — c·cos \alpha — d·cos \beta \]

Формулы боковых сторон трапеции через высоту и углы при нижнем основании:

\[ с = \dfrac{h}{sin \alpha } , d = \dfrac{h}{sin \beta } \]

Формулы длины средних линий трапеции

Формула определения длины средней линии через длины оснований:

\[ m = \dfrac{a + b}{2} \]

Формула определения длины средней линии через площадь и высоту:

\[ m = \dfrac{S}{h} \]

Формулы длины высоты трапеции

Формула высоты трапеции через сторону и прилегающий угол при основании:

\[ h = c·sin α = d·sin β \]

Формула высоты трапеции через диагонали и углы между ними:

\[ h = sin γ \cdot \dfrac{d_1\cdot d_2}{a + b} = sin δ \cdot \dfrac{d_1\cdot d_2}{a + b} \]

Формула высоты трапеции через диагонали, углы между ними и среднюю линию:

\[ h = sin γ \cdot \dfrac{d_1 \cdot d_2}{2m 2m} = sin δ · \dfrac{d_1}{d_2} \]

Формула высоты трапеции через площадь и длины оснований:

\[ h = \dfrac{2S}{a + b} \]

Формула высоты трапеции через площадь и длину средней линии:

\[ h = \dfrac{2S}{m} \]

Формулы длин диагоналей трапеции

Формулы длин диагоналей трапеции по теореме косинусов:

\[ d_1 = \sqrt{a^2 + d^2 — 2ad·cos β} \]

\[ d_2 = \sqrt{a^2 + c^2 — 2ac·cos β} \]

Формулы длин диагоналей трапеции через четыре стороны:

\[ d_1 = \sqrt{d^2 + ab — \dfrac{a(d^2 — c^2)}{a — b} } \]

\[ d_2 = \sqrt{c^2 + ab — \dfrac{ a(c^2 — d^2) }{a — b} } \]

Формулы длин диагоналей трапеции через высоту:

\[ d_1 = \sqrt{h^2 + (a — h · ctg β)^2} = \sqrt { h^2 + (b + h · ctg α)^2} \]

\[ d_2 = \sqrt{h^2 + (a — h · ctg α)^2} = \sqrt{h^2 + (b + h · ctg β)^2} \]

Формулы длин диагоналей трапеции через сумму квадратов диагоналей:

\[ d_1 = \sqrt{c^2 + d^2 + 2ab — d_2^2} \]

\[ d_2 = \sqrt{c^2 + d^2 + 2ab — d_1^2} \]

Формулы площади трапеции

Формула площади трапеции через основания и высоту:

\[ S = \dfrac{ (a + b) · h }{2} \]

Формула площади трапеции через среднюю линию и высоту:

\[ S = m · h \]

Формула площади трапеции через диагонали и угол между ними:

\[ S = \dfrac{d_1d_2}{2} · sin γ = \dfrac{d_1d_2}{2} · sin δ \]

Формула площади трапеции через четыре стороны:

\[ S = \dfrac{a + b}{2}\sqrt{c^2 — \left\lgroup\dfrac{(a — b)^2 + c^2 — d^2)}{2\cdot (a — b)} \right\rgroup ^2 } \]

Формула Герона для площади трапеции

\[ S = \frac{a + b}{\left|a-b\right| } \sqrt{(p — a)(p — b)(p — a — c)(p — a — d)} \]

где \( p = \dfrac{a + b + c + d}{2} \) — полупериметр трапеции.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!