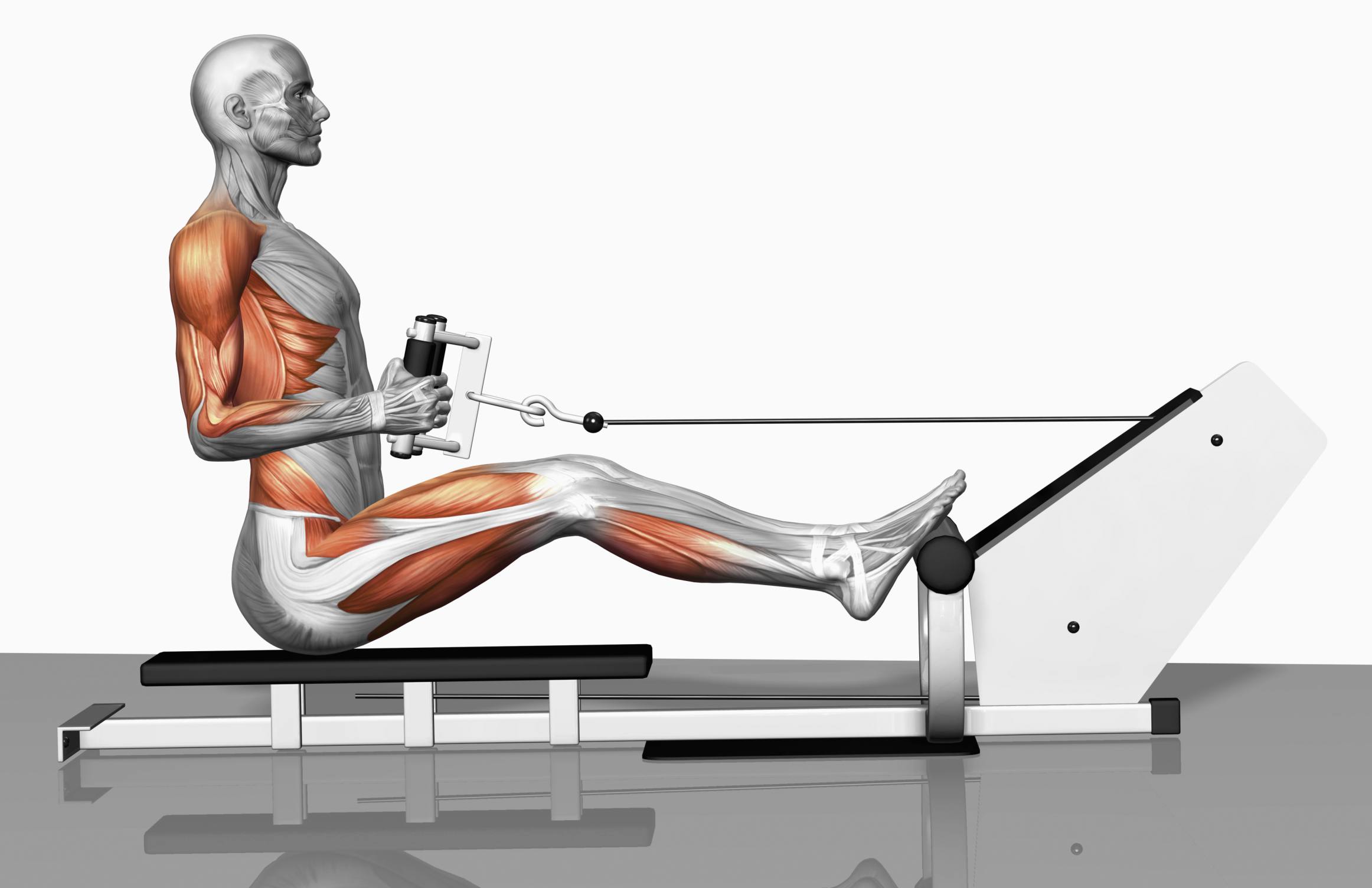
Тяга нижнего блока к поясу: Недопустимое название

Содержание

Тяга к поясу нижнего блока: описание и техника упражнения

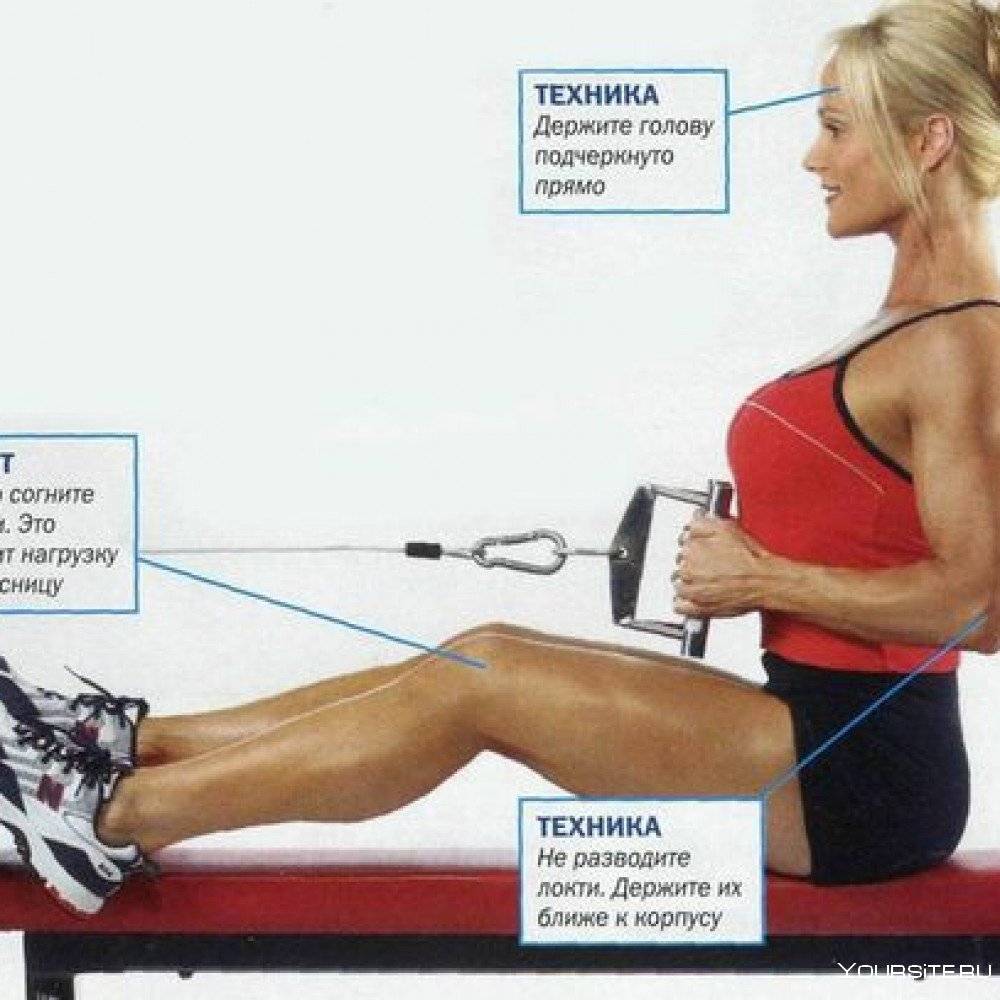
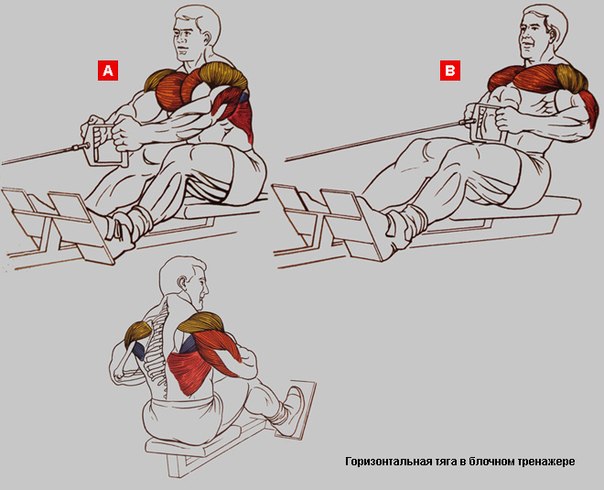
Тяга к поясу нижнего блока является базовым упражнением. Оно активирует довольно много мышечных групп. При этом целевой являются широчайшие мышцы спины. А второстепенные группы представлены: грудными мускулами, бицепсом, плечом, нижними мышцами спины, квадрицепсами и разгибателями бедра, а также предплечьем.

Считается, что данное упражнения лучше всего подходит тем, кто хочет сделать свою спину шире. Наиболее эффективным вариантом упражнения считается модификация с применением раздвоенной рукояти, которая позволяет держать кисти параллельно друг другу. С точки зрения анатомии, упражнение относится к горизонтальным тягам. Оно выполняется в положении сидя и по природе движения напоминает греблю.

А теперь давайте поближе познакомимся с упражнением под названием тяга к поясу нижнего блока.

Подготовка

Данное упражнение требует выполнения некоторых условий:

Высота скамьи или сидения должна быть такой, чтобы трос при выполнении тяги был параллелен полу.
Тело ни в коем случае не должно сползать вперед, а значит, у ступней должна быть удобная опора.
Рукоятки могут быть как фиксированными на общем основании, так и отделенными друг от друга.
Так или иначе, желательно, чтобы при выполнении тяги ладони смотрели друг на друга.

Итак, для начала нужно сесть на скамью и взять в руки рукоятки. Затем стоит подтянуть их к себе до тех пор, пока спина не примет вертикальное положение, с сохранением ее естественного изгиба в районе лопаток. При этом руки должны быть ровными. Это и есть исходное положение.

Теперь нужно вдохнуть, задержать дыхание и начать тягу:

Первая фаза движения (она же промежуточная) заканчивается в момент, когда локти окажутся на одной линии с туловищем, а угол изгиба локтевого сустава будет близок к прямому.
Дальше рукоять тянется чуть ближе к поясу таким образом, чтобы локти вышли назад за пределы туловища. Здесь начинается вторая фаза.
Из данного положения нужно максимально сильно отвести плечи назад и постараться сдвинуть лопатки. 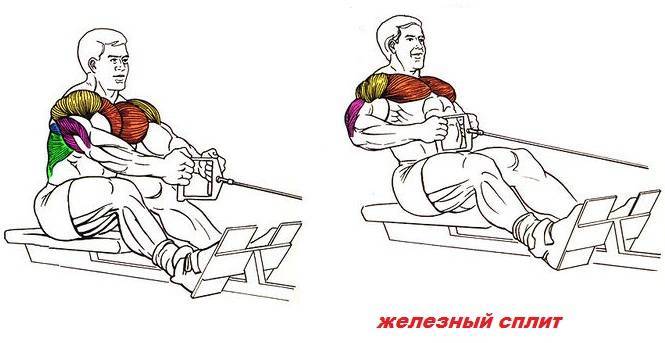Чем более сильного сокращения широчайших мышц спины вы добьетесь на этой стадии, тем эффективнее будет упражнение.
Затем нужно быстро выдохнуть и вернуть рукоятки в исходное положение, сохраняя спину прямой и неподвижной.

При работе с большим весом можно использовать кистевые ремни.

Ошибки и нюансы

Выполняя такое упражнение, как тяга к поясу нижнего блока, нужно следить, чтобы локти были прижаты к телу. Если они расставлены в стороны, ни к чему хорошему это не приведет. Именно благодаря прижатым к туловищу локтям и максимально отведенным назад лопаткам данное упражнение позволяет хорошо нагрузить широчайшие мышцы спины, а точнее, их нижнюю часть.

Если развести локти в стороны, нагрузка сместится на верхнюю часть спины, средние пучки трапециевидных мышц и ромбовидные мускулы. Таким образом, упражнение просто не будет выполнять своей главной задачи.

Туловище, как уже говорилось, должно на протяжении всего движения быть вертикальным. Однако небольшие отклонения в начале и в конце движения допустимы. Они не должны превышать 10 градусов. Ограниченная амплитуда туловища обуславливается необходимостью в подстраховке от травм нижней части позвоночника.

Упражнение можно делать и с прямой перекладиной, то есть ладони будут смотреть вниз, а не друг на друга. Если, взявшись за перекладину, направить локти в стороны и вверх, то в работе будут задействованы средняя часть трапециевидной мышцы, задняя часть дельтовидной мышцы и ромбовидный мускул.

Если перекладина имеет посредине изгиб, а ее концы обращены назад, то, направив локти вниз и к туловищу, можно практически полностью исключить из работы дельты. А вот если локти направить вверх и в стороны, то дельты будут участвовать в движении весьма активно. Оба варианта хорошо нагружают трапецию и ромбовидную мышцу.

Получается, что тяга к поясу нижнего блока при разных положениях локтей и использовании различных перекладин позволяет глубоко проработать все мышцы спины: широчайшие, ромбовидные, трапециевидные, круглые и, наконец, задний пучок дельтовидных мышц плеча.

Заключение

Как можно заметить, тяга нижнего блока к поясу рукой, а точнее, руками, несмотря на кажущуюся простоту, имеет ряд важных нюансов. Лишь осознав их и поработав над правильной техникой, можно достичь хороших результатов. Альтернативой данного упражнения является тяга штанги к поясу в положении стоя в наклоне. В спортивной литературе часто можно встретить фразу «тяга нижнего блока/штанги к поясу» и, несмотря на то, что эти упражнения схожи с анатомической точки зрения, они сильно отличаются друг от друга в плане техники.

Тяга нижнего блока к животу узким хватом в Химках: 516-товаров: бесплатная доставка, скидка-13% [перейти]

Партнерская программаПомощь

Химки

Каталог

Каталог Товаров

Одежда и обувь

Стройматериалы

Здоровье и красота

Продукты и напитки

Текстиль и кожа

Детские товары

Электротехника

Сельское хозяйство

Мебель и интерьер

Промышленность

Вода, газ и тепло

Все категории

ВходИзбранное

231 000

Тяга нижнего блока Realleader M2-1018 Производитель: Realleader

ПОДРОБНЕЕ

163 800

Тяга нижнего блока Protrain 61A13-80 Производитель: Protrain

ПОДРОБНЕЕ

114 800

Тяга нижнего блока Impact CT2025 Производитель: Impact, Вес стека: 91 кг

ПОДРОБНЕЕ

163 800

Тяга нижнего блока Protrain 61A13-80 Производитель: Protrain

ПОДРОБНЕЕ

237 300

Тяга нижнего блока Protrain 7313 Производитель: Protrain

ПОДРОБНЕЕ

Тяга блочная Hawk IR-038-1 Производитель: Hawk, Тип комплектующей: трос, Группа мышц: руки, спина

ПОДРОБНЕЕ

32 990

Опция Верхняя тяга Body Solid LA-78/GLA-78 Производитель: Body Solid, Группа мышц: грудь, плечи,

ПОДРОБНЕЕ

63 000

Вертикальная тяга + разгибание ног + тяга ARMS075 s-dostavka Производитель: V-Sport

ПОДРОБНЕЕ

177 161

A3033 Гребная тяга (горизонтальный блок) Long Pull (109 кг), DHZ Производитель: DHZ, Вес стека: 109

ПОДРОБНЕЕ

146 235

JOHNS Горизонтальная тяга Johns CT2025 Производитель: Johns, Тип нагрузки: грузоблок, Упражнения:

ПОДРОБНЕЕ

Тяга блочная Onhillsport R5 Производитель: Onhillsport, Группа мышц: руки

ПОДРОБНЕЕ

259 000

Верхний блок/тяга к поясу AnyFit PS02-96 Вес стека: 52 кг

ПОДРОБНЕЕ

-21%

-65%

-19%

-67%

Узкий хватНижний блок

Рукоятка для тяги к животу (узкий параллельный хват) Voitto, обрезиненная, A-5057 Вес: 2.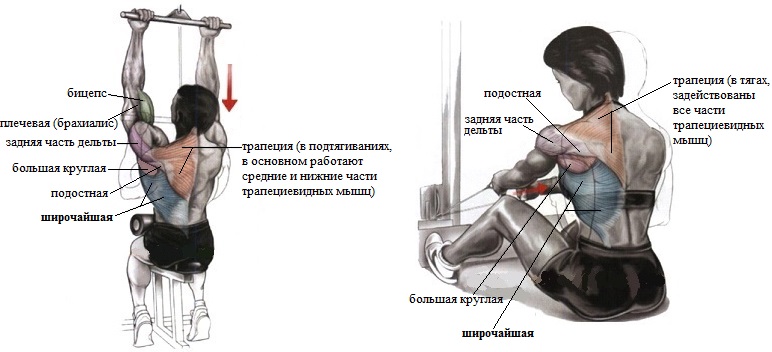 00000000

ПОДРОБНЕЕ

Рукоятка для тяги к животу CT504 Производитель: Без бренда, Назначение: для тяги, Тип

ПОДРОБНЕЕ

Рукоятка для тяги к животу (узкий параллельный хват) ZSO Производитель: ZSO, Назначение: для тяги,

ПОДРОБНЕЕ

Ручка для тяги к животу МВ 5.02 Производитель: MB Barbell, Назначение: для тяги, Тип комплектующей:

ПОДРОБНЕЕ

Рукоятка для тяги на трицепс и тяги к животу Производитель: HASTTINGS, Тип комплектующей: рукоятка

ПОДРОБНЕЕ

Рукоятка для тяги к животу (узкий параллельных хват) Тип комплектующей: рукоятка, Вид рукояти для

ПОДРОБНЕЕ

Рукоятка для тяги к животу обрезиненная Hasttings Digger HD61F1B Производитель: HASTTINGS,

ПОДРОБНЕЕ

Рукоятка для тяги к животу (узкий параллельный хват), ZSO-6006 Производитель: ZSO, Тип

ПОДРОБНЕЕ

Рукоятка для тяги к животу Hasttings Digger HD61F1B Производитель: HASTTINGS, Назначение: для тяги,

ПОДРОБНЕЕ

Рукоятка для тяги к животу металлическая узкий параллельный хват Производитель: Original FitTools,

ПОДРОБНЕЕ

Ручки для тяги Torneo A-100PH, Черный Цвет: черный, Производитель: Torneo, Назначение: для тяги

ПОДРОБНЕЕ

-14%

3 709

4290

Рукоятка для тяги к животу (узкий параллельный хват) OFT FT-RSBG

ПОДРОБНЕЕ

2 страница из 18

Тяга нижнего блока к животу узким хватом

Проблемы со шкивом

На этой странице я собрал коллекцию задач со шкивами, чтобы помочь вам лучше понять системы шкивов.

Необходимые уравнения и справочная литература для решения этих проблем приведены на странице трения, странице равновесия и странице второго закона Ньютона.

Проблема №1

Брусок массой м тянут с помощью шкива с постоянной скоростью по поверхности, наклоненной под углом θ . Коэффициент кинетического трения равен 9.0009 μ _k , между блоком и поверхностью. Определить тяговое усилие F . Ответ: мг cos θ μ _k + мг sin θ

Проблема № 2

Два блока массой м и м висят на одном шкиве, как показано на рисунке. Определить ускорение блоков. Не учитывать массу шкива.

Подсказка и ответ

Проблема № 3

Два блока массой м и м соединены шкивом, как показано на рисунке. Коэффициент статического трения между блоком и поверхностью составляет мкс _с .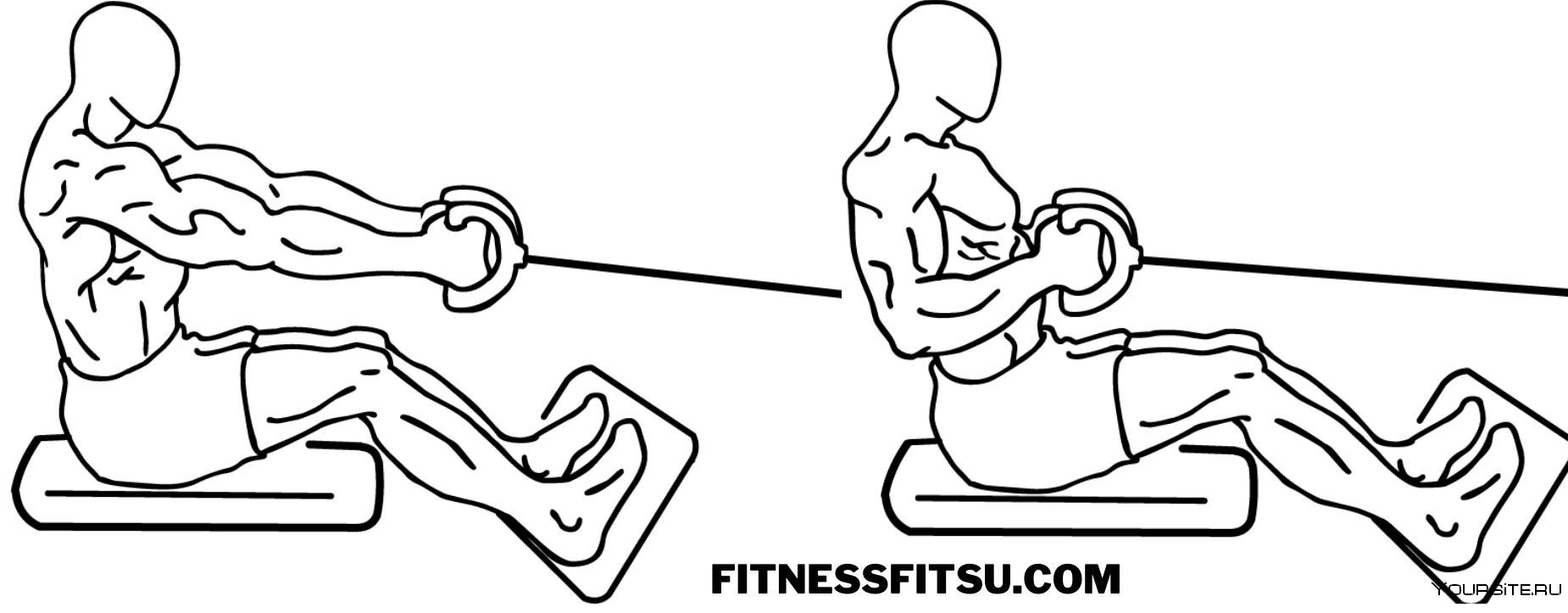 Какова максимальная масса m , чтобы не происходило скольжения? Ответ: максимум м = м мк _с

Проблема № 4

Два блока массой м и M соединены шкивом, как показано на рисунке. Коэффициент статического трения между блоком и поверхностью составляет мкс _с . Какова минимальная и максимальная масса M , чтобы не происходило скольжения?

Подсказка и ответ

Проблема № 5

Два блока массой м и м соединены шкивом, как показано на рисунке. Коэффициент статического трения

мк _s , между блоками и поверхностью. Какова максимальная масса m , чтобы не происходило скольжения? Ответ: Максимум м = М μ _с /(sin θ − cos θ μ _с 9001 0 )
Проблема № 6

Два блока массой м и м соединены шкивом, как показано на рисунке. Коэффициент статического трения между левым блоком и поверхностью равен 9.0009 µ _с1 , а коэффициент трения покоя между правым блоком и поверхностью равен µ _с2 . Сформулируйте математическое неравенство для условия отсутствия скольжения. Неравенств может быть больше одного.

Подсказка и ответ

Проблема № 7

Блок массой м тянут с помощью двух шкивов, как показано, с постоянной скоростью вдоль поверхности, наклоненной под углом

θ . Коэффициент кинетического трения равен 9.0009 μ _k , между блоком и поверхностью. Определить тяговое усилие F . Не учитывать массу шкивов.

Подсказка и ответ

Проблема № 8

Блок массой м поднимается с постоянной скоростью с помощью двух шкивов, как показано на рисунке. Определить тяговое усилие F . Не учитывать массу шкивов.

Подсказка и ответ

Проблема № 9

Блок массой M поднимается с постоянной скоростью с помощью шкивов, как показано на рисунке. Определить тяговое усилие F . Не учитывать массу шкивов.

Подсказка и ответ

Советы и ответы на эти проблемы со шкивами будут даны далее.

Советы и ответы по проблемам со шкивом

Подсказка и ответ на Задачу №2

Это называется машиной Этвуда и обычно используется для демонстрации на уроках физики.

Примените второй закон Ньютона к блоку слева. У нас есть Mg − T = млн лет (принимая нисходящее направление за положительное). Примените второй закон Ньютона к блоку справа. Имеем мг — Т = — мА (ускорение двух блоков имеет противоположные знаки, так как один движется вверх, а другой вниз). Объедините эти два уравнения, и мы сможем найти выражение для ускорения блоков.

Ответ: a = ( M − m ) г / ( M + m )

Подсказка и ответ на Задачу №4

Для максимальной массы M блок находится на грани соскальзывания вниз по склону. Это означает, что

Mg sin θ − T − Mg cos θ μ _s = 0, где T 90 010 — натяжение веревки. Поскольку T = мг , мы можем вычислить максимум M из предыдущего уравнения.
При минимальной массе M блок находится на грани соскальзывания вверх по склону. Это означает, что Mg sin θ − T + Mg cos θ μ _s = 0, где T 90 010 = мг . Мы можем рассчитать минимум M из предыдущего уравнения.
Ответ: Минимум M = m /(sin θ +cos θ μ _с ), максимум M = м /(sin θ −cos θ μ _с )
Подсказка и ответ на Задачу №6
Это сложная задача! Мне потребовалось некоторое время, чтобы понять это!
Под некоторым углом θ ₁ > θ _max1 блок M соскользнет вниз сам по себе, если к нему не привязана веревка.
Аналогично, под некоторым углом θ ₂ > θ _max2 блок м соскользнет вниз сам по себе, если веревка не привязана.
Известно, что θ _max1 = atan( μ _s1 ) и θ _max2 = atan( μ _с2 ).
If θ ₁ ≤ θ _max1 и θ ₂ ≤ θ _max2 , то скольжение не происходит. Осталось рассмотреть еще три случая.
Случай 1:
θ ₁ > θ _макс.1 и θ ₂ ≤ θ _{макс.2 9 0015} .
Примените уравнение равновесия к блоку M , в котором он находится на грани соскальзывания вниз. Имеем: Mg sin θ ₁

− Mg cos θ ₁ μ _s1 − T _мин1 = 0, где T _мин1 соответствует минимальному натяжению каната, препятствующему соскальзыванию блока M вниз. (Обратите внимание, что система естественным образом «устанавливается», так что натяжение каната T , необходимое для предотвращения скольжения блока, является минимально возможным). При T < T _min1 блок соскальзывает вниз. Из этого уравнения получаем T _мин1 = Mg sin θ ₁ − Mg cos θ ₁ мк _с1 . Назовите это уравнение (1).
Нет необходимости рассматривать блок M скольжение вверх, так как это невозможно для θ ₂ ≤ θ _max2 (что означает, что блок
m не может скользить вниз, что означает, что он не может тянуть блок М вверх).
T _min1 должен быть обеспечен блоком м и не должен превышать максимальное натяжение каната, которому может противостоять блок м и не подтягиваться по склону. Это максимальное натяжение каната можно определить из следующего уравнения равновесия, примененного к блоку м : мг sin θ ₂ + мг cos θ ₂ 90 009 мк _с2 − Т _max2 = 0, откуда T _max2 = мг sin θ ₂ + мг cos θ ₂ мк _с2 . Назовите это уравнение (2).
Для без скольжения T _мин1 ≤ T
макс2 . Следовательно, из уравнений (1) и (2) имеем окончательное неравенство для этого случая:
M sin θ ₁ − M cos θ ₁ μ _{s1 9001 5} ≤ м sin θ ₂ + м cos θ ₂ мк _с2
Случай 2:
θ ₁ ≤ θ _макс.1 и θ ₂ > θ _{макс.2 9 0015} .
То же, что и случай 1, по симметрии. Следовательно, окончательное неравенство для этого случая:
м sin θ ₂ − м cos θ ₂ μ _{s2 9001 5} ≤ M sin θ ₁ + M cos θ ₁ μ _с1
Случай 3:
θ ₁ > θ _макс.
1 и θ ₂ > θ _{макс.2 90 015} .
Блоки будут скользить вместе в одном или другом направлении. Чтобы определить направление, мы должны сначала рассчитать результирующую силу, тянущую вниз каждый блок вдоль соответствующих наклонов под действием силы тяжести. Мы делаем это следующим образом:

Для блока M , F _net1 = Mg sin θ ₁ − Mg cos 9000 9 θ ₁ μ _с1 . И F _net1 > 0, так как θ ₁ > θ _max1 .

Для блока м , F _net2 = мг sin θ ₂ − мг cos θ ₂ мк _с2 . И F _net2 > 0, так как θ ₂ > θ _max2 .

Теперь нам нужно рассмотреть три дополнительных случая. Окончательные неравенства для этого случая будут даны в этих трех подслучаях следующим образом.

Случай 3A:

Если F _net1 = F _net2 блоки не будут скользить.

Случай 3B:

Если F _net1 > F _net2 , то F _net1 ≤ мг sin θ ₂ + мг cos θ ₂ μ _s2 без скольжения. Обратите внимание, что F _net1 равно натяжению каната, и это натяжение каната является минимальным, необходимым для предотвращения скольжения блока M по склону.

Следовательно, для отсутствия скольжения: M sin θ ₁ − M cos θ ₁ μ _s1 ≤ м 9 0010 sin θ ₂ + м cos θ ₂ мк _с2

Случай 3C:

Если F _net2 > F _net1 , то F _net2 ≤ Mg sin θ ₁ + Mg cos θ ₁ μ _s1 для отсутствия скольжения. Обратите внимание, что F _net2 равно натяжению каната, и это натяжение каната является минимальным, необходимым для предотвращения скольжения блока м по склону.

Отсюда для отсутствия скольжения: м sin θ ₂ − м cos θ ₂ μ _{с 2} ≤ M sin θ ₁ + M cos θ ₁ мк _с1

Готово!

Подсказка и ответ на Задачу №7

Примените к блоку условие статического равновесия. Имеем 2 F − мг sin θ − мг cos θ μ _k = 0. Член 2 F 9 0010 исходит из силового анализа, в котором мы видим, что есть два отрезки веревки одинаково натягиваются на блок. Затем мы решаем это уравнение для F .

Ответ: F = (1/2) мг (sin θ + μ _k cos θ )

Подсказка и ответ на Задачу №8

Примените к блоку условие статического равновесия. У нас есть 2 F − мг = 0. Член 2 F получен из анализа силы, в котором мы видим, что есть два сегмента веревки, одинаково натягивающие блок. Затем мы решаем это уравнение для F .

Ответ: F = мг /2

Подсказка и ответ на Задачу №9

При ближайшем рассмотрении мы видим, что два нижних шкива удерживаются четырьмя отрезками веревки. Натяжение веревки считается одинаковым по всей ее длине (хорошее предположение для веревок в целом, поскольку они мало весят). Три из четырех отрезков веревки расположены вертикально, а оставшийся отрезок веревки находится под небольшим углом к вертикали. Но для простоты вычислений мы можем считать его строго вертикальным. Поскольку мы пренебрегаем массой шкивов, натяжение четырех отрезков веревки должно равняться весу массы, чтобы выполнялось условие статического равновесия. Следовательно, 4 F − Mg = 0. Затем мы решаем это уравнение для F .

Ответ: F = Mg /4

Бонусная задача
Ленточный конвейер, несущий агрегат, показан на рисунке ниже. Двигатель вращает верхний ролик с постоянной скоростью, а остальные ролики могут вращаться свободно. Лента наклонена под углом θ . Чтобы удерживать ремень в натянутом состоянии, к ремню подвешен груз массой м , как показано на рисунке.
Найдите точку максимального натяжения ремня. Вам не нужно его вычислять, просто найдите место и объясните причину.
Вы можете получить решение для этого в формате PDF. Он доступен по этой ссылке
Вернуться на страницу Вопросы по физике
Вернуться на домашнюю страницу Real World Physics Problems
Регулировка натяжения ремня (MK3/MK3S/MK3S+/MK4) | База знаний Prusa
Актуально для
:
MK2.5MK2.5SMK3MK3SMK3S+MK4
Последнее обновление
3 месяца назад
привести к сбоям в работе принтера и препятствовать правильной печати. Это может привести к сдвигу слоя, появлению ореолов или другим аномалиям печати, таким как получение неправильной формы вместо идеального круга при печати цилиндра. Ремень оси Y расположен под нагревательным столом, ремень оси X перемещает печатающую головку. Все регулировки выполняются шестигранным ключом на 2,5 мм.
Проверка натяжения ремня
На MK3/S/+ запустите самопроверку или проверку ремня в меню «Калибровка» на ЖК-дисплее. Затем проверьте ЖК-меню -> Поддержка -> Статус пояса. Вам нужен номер от 260 до 290 (275~) . Чем меньше число, тем туже натянут ремень. Представьте, что это фиктивное количество зубов в обращении.
Для MK2.5 и MK2.5S отличный способ проверить правильность натяжения ремня — распечатать этот измеритель натяжения для ремней GT2.
Другой способ — использовать метод, описанный в этом шаге руководства по сборке, чтобы проверить, правильно ли натянут шкив и не слишком ли ослаблен ремень. Удерживайте вал двигателя оси X плоскогубцами (воспользуйтесь плоской частью вала), чтобы зафиксировать его на месте ( фиолетовый кружок ), затем попробуйте переместить экструдер вручную. Лента не должна провисать в результате нажатия на экструдер. Та же процедура может быть применена для проверки шкива оси Y и ремня.
Ремень оси X
Незначительные регулировки MK3S
Ослабьте два передних винта и убедитесь, что справа от них есть место для перемещения ( желтые кружки ). Помогая вращению двигателя рукой, затяните винт M3x18 в верхней части двигателя на конце X ( фиолетовая стрелка ).
После каждого или двух оборотов проверяйте натяжение ремня, сжимая их вместе. Для оптимальной работы ремень должен сжиматься пальцами с некоторым усилием (зеленые стрелки). Переместите экструдер до упора на концевой ролик X и проверьте натяжение ремня посередине оси X.
Незначительные регулировки MK3S+, MK4
Слегка отпустите все винты, удерживающие двигатель, иначе «натяжитель» не сработает, так как двигатель должен двигаться (левый рисунок).
С помощью шестигранного ключа начните затягивать винт на задней стороне двигателя с Х-образной головкой, но после каждого или двух оборотов проверяйте натяжение ремня (правый рисунок).
Когда вы добьетесь оптимального натяжения, снова затяните винты (левый рисунок).
Большие регулировки MK3/S/+
Если небольшой регулировки недостаточно, необходимо отрегулировать ее на держателе ремня. Он находится на задней части экструдера и требует небольшой разборки.
Сначала снимите два верхних винта с держателя мотора, чтобы ремень немного провисал и им было легче манипулировать.
Отрежьте стяжки на задней части экструдера ( красные стрелки ), которые крепят провода хотэнда и , которые крепят обертку кабеля.
Отвинтите 4 винта, обведенных на рисунке ниже.
Осторожно снимите заднюю панель, убедившись, что провода не повреждены, и поверните всю пластину влево или вправо.
Теперь у вас есть доступ к местам крепления ремней. Поставьте отметку на ремне ручкой или маркером как можно ближе к пластиковой части, чтобы вы знали, как он был отрегулирован. Теперь выньте ремень из крепления и переместите его на 1-2 зуба.
Возможно, потребуется срезать последний зуб ремня.
Установите заднюю панель на место, затяните винты, начиная с центрального для выравнивания, затем наденьте новые стяжки.
Снова затяните винты на x-двигателе, чтобы закрепить его. При необходимости отрегулируйте его сильнее.
Большие регулировки MK4
Ослабьте три указанных винта, закрывающие Х-каретку. Осторожно выньте заднюю крышку X.
Теперь у вас есть доступ к месту крепления ремня. Поставьте отметку на ремне ручкой или маркером как можно ближе к пластиковой части, чтобы вы знали, как он был отрегулирован. Теперь выньте ремень из крепления и переместите его на 1-2 зуба.
Ремень оси Y
Незначительные корректировки
На передней панели корпуса принтера, за ЖК-модулем, вы найдете распечатанный натяжитель ремня оси Y. Он удерживается двумя винтами M3X10 (, фиолетовая стрелка, ), проходящим через переднюю панель.
Если у вас есть зазор между натяжной частью и передней пластиной рамы ( синие стрелки ), вы можете натянуть ремень с помощью шестигранного ключа на 2,5 мм, повернув винты по часовой стрелке ( фиолетовая стрелка ), закрывая пробел.
Проще всего получить доступ к винтам снизу, переместив принтер к краю стола так, чтобы ЖК-модуль выступал наружу. Теперь у вас есть доступ к болтам снизу ЖК-модуля.
Большие регулировки
Если небольшой регулировки недостаточно, вы должны отрегулировать ее на держателе ремня. Существует два основных типа держателей ремня оси Y: регулируемый и фиксированный. Регулируемый держатель ремня был представлен в первом квартале 2019 года. , с S-обновлением для оригинальной Prusa MK3, а также присутствует на оригинальной Prusa MK4. Регулировки для этого объясняются в « Method 1 ». Для более ранней модели Original Prusa MK3 следуйте « Method 2 » для фиксированного держателя ремня.
Способ 1. Регулируемый держатель ремня
Оригинальный Prusa MK4 имеет другой дизайн, чем на изображениях, но процедура такая же.
Отсоедините принтер от сети и положите его сбоку от блока питания.
Под кареткой кровати вы найдете держатель для ремня. Ослабьте правый винт, повернув его против часовой стрелки ( оранжевый круг левое изображение).
Поверните винт, проходящий через две половины держателя ремня ( фиолетовая стрелка правое изображение). Поверните по часовой стрелке , чтобы натянуть ремень, сдвинув две половинки вместе ( синие стрелки ).
При правильном натяжении снова закрепите правую половину держателя ремня, повернув винт из шага 2 по часовой стрелке ( оранжевый кружок левое изображение).
Способ 2 — Фиксированный держатель ремня
Отсоедините принтер от сети и положите его сбоку от блока питания.
Отсоедините натяжитель ремня, чтобы облегчить управление ремнем ( фиолетовые стрелки ). Полное отсоединение натяжителя может и не понадобиться, но это облегчит регулировку ремня на следующем шаге.
Поставьте отметку на ремне, чтобы знать, насколько вы его перемещаете. Теперь выньте ремень из верхнего слота и переместите его на 1-2 зуба (, синяя стрелка, ), прежде чем вставить его обратно в слот (, зеленые стрелки, ).
Ваше крепление на ремне может выглядеть немного по-другому, поскольку это другая итерация, но процедура остается прежней.
Закрепите натяжитель ремня двумя винтами M3x10 через раму ( фиолетовая стрелка ).