Трапеция правильная: Равнобедренная трапеция — урок. Геометрия, 8 класс.

Трапеция. Формулы, признаки и свойства трапеции

Навигация по странице: Определение трапеции Элементы трапеции Виды трапеций Основные свойства трапеции Стороны трапеции Средняя линия трапеции Высота трапеции Диагонали трапеции Площадь трапеции Периметр трапеции Окружность описанная вокруг трапеции Окружность вписанная в трапецию Другие отрезки трапеции

Определение.

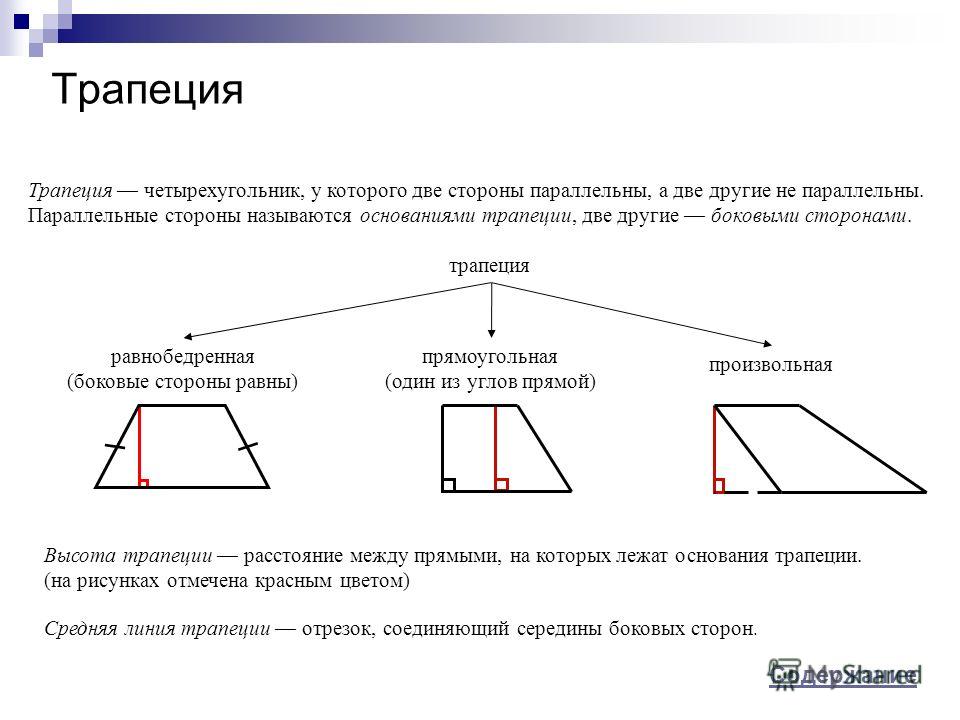
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

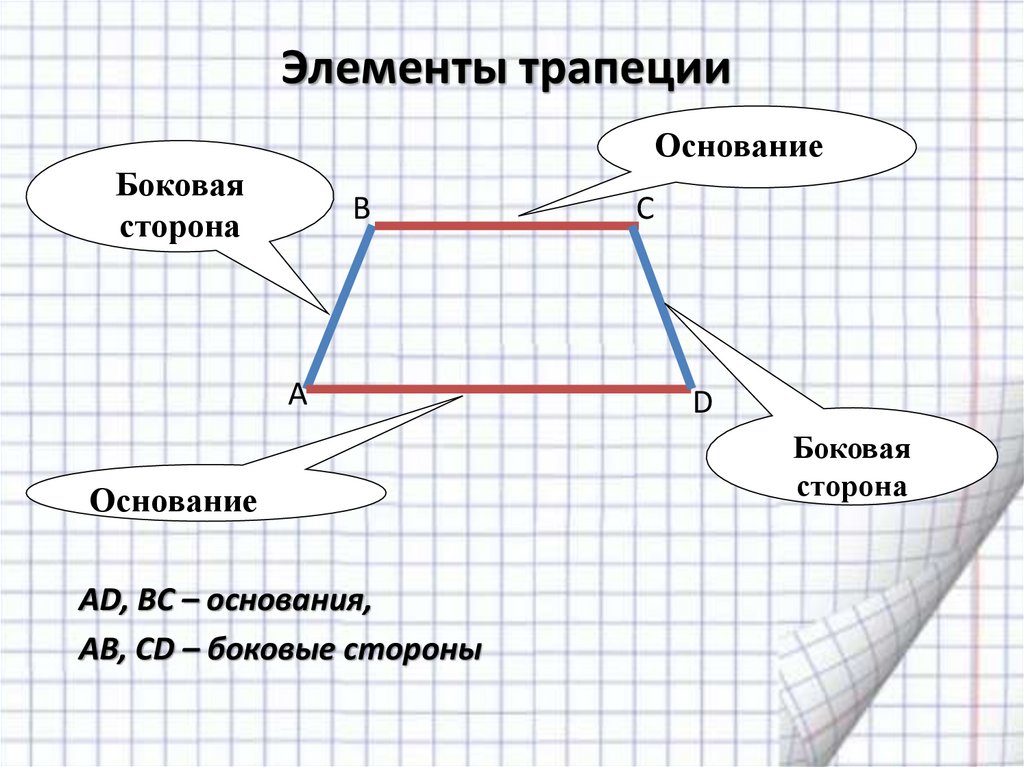
Элементы трапеции:

• Основы трапеции — параллельные стороны
• Боковые стороны — две другие стороны
• Средняя линия — отрезок, соединяющий середины боковых сторон.

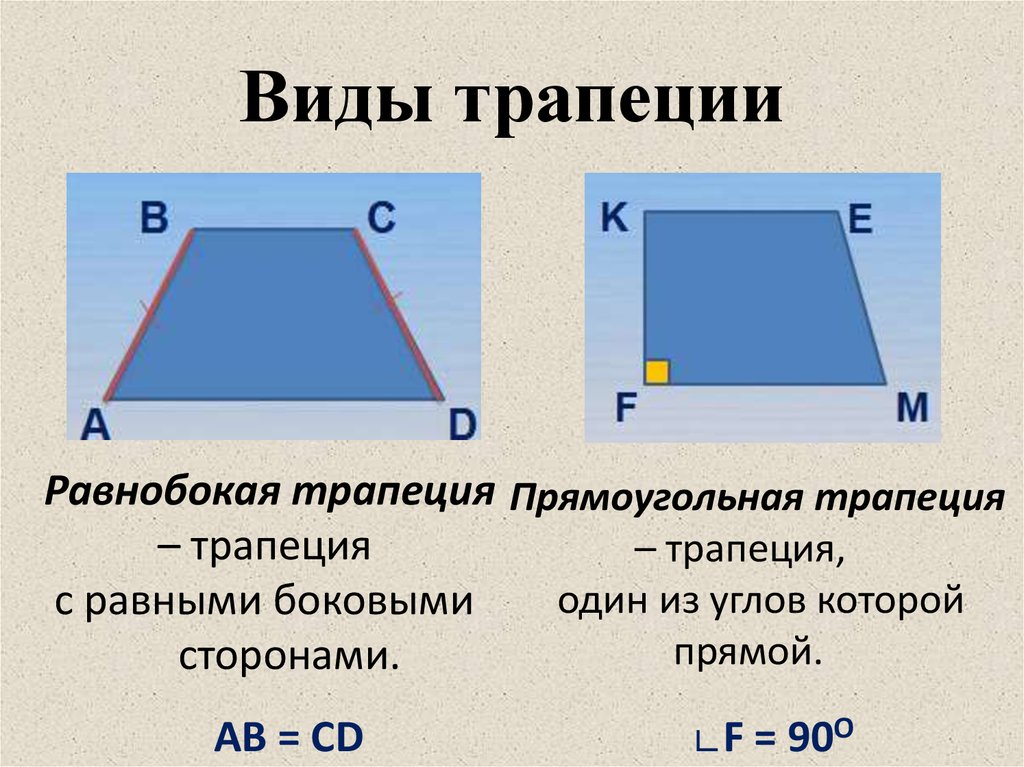
Виды трапеций:

• Равнобедренная трапеция — трапеция, у которой боковые стороны равны
• Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам

Рис.1		Рис.2

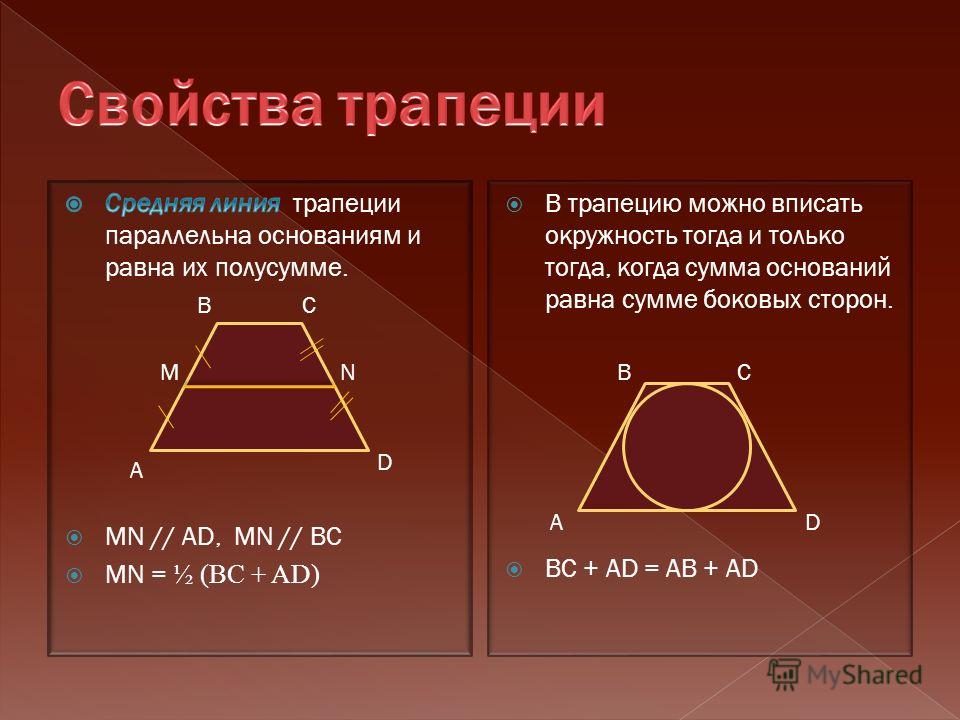
Основные свойства трапеции

1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

m =	a + b
	2

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m — b

b = 2m — a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a — h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a — c·cos α — d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Средняя линия трапеции

Определение.

Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

m =	a + b
	2

2. Формула определения длины средней линии через площадь и высоту:

m =	S
	h

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d1 d2	=	sin δ ·	d1 d2
		a + b			a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d1 d2	=	sin δ ·	d1 d2
		2m			2m

4. Формула высоты трапеции через площадь и длины оснований:

h =	2S
	a + b

5. Формула высоты трапеции через площадь и длину средней линии:

h =	S
	m

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² — 2ad·cos β

d₂ = √a² + c² — 2ac·cos α

2. Формулы диагоналей через четыре стороны:

d1 =	√	d 2 + ab —	a(d 2 — c2)
			a — b

d2 =	√	c2 + ab —	a(c2 — d 2)
			a — b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a — h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a — h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab — d₂²

d₂ = √c² + d ² + 2ab — d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

S =	(a + b)	· h
	2

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d1d2	· sin γ	=	d1d2	· sin δ
	2			2

4. Формула площади через четыре стороны:

S =	a + b	√	c2 —	(	(a — b)2 + c2 — d 2	)	2
	2				2(a — b)

5. Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
	|a — b|

где

p =	a + b + c + d	— полупериметр трапеции.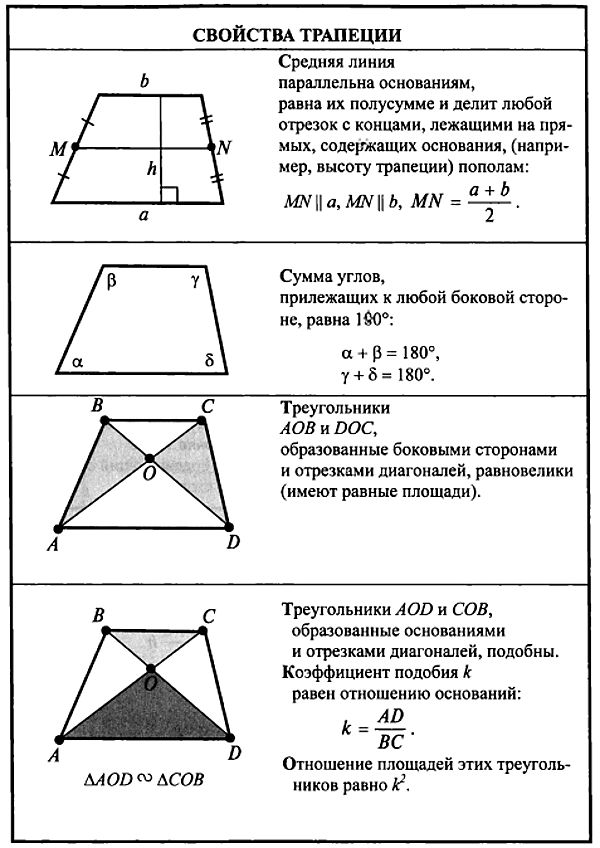
	2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где

p =	a + c + d1
	2

a — большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

r =	h
	2

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Все таблицы и формулы

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Навигация по странице: Определение равнобедренной трапеции Признаки равнобедренной трапеции Основные свойства равнобедренной трапеции Стороны равнобедренной трапеции Средняя линия равнобедренной трапеции Высота равнобедренной трапеции Диагонали равнобедренной трапеции Площадь равнобедренной трапеции Окружность описанная вокруг равнобедренной трапеции

Формулы и свойства трапеции

Определение.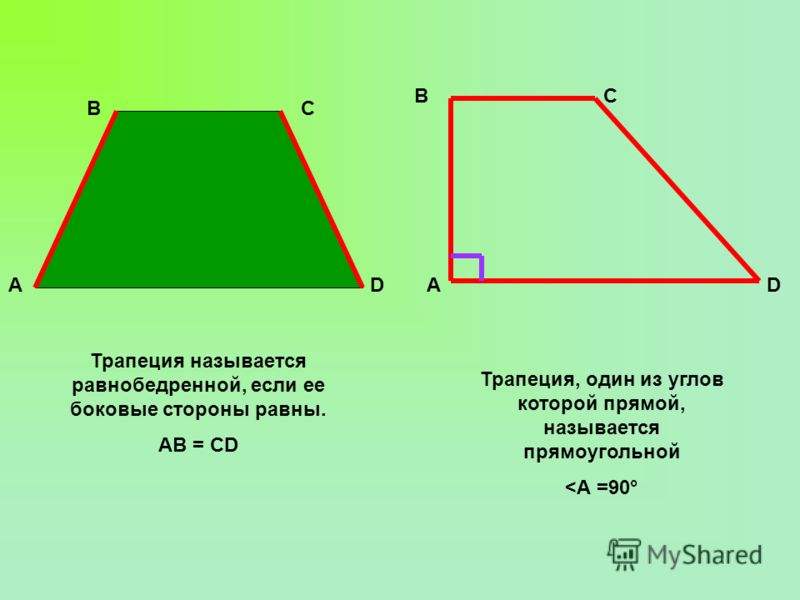

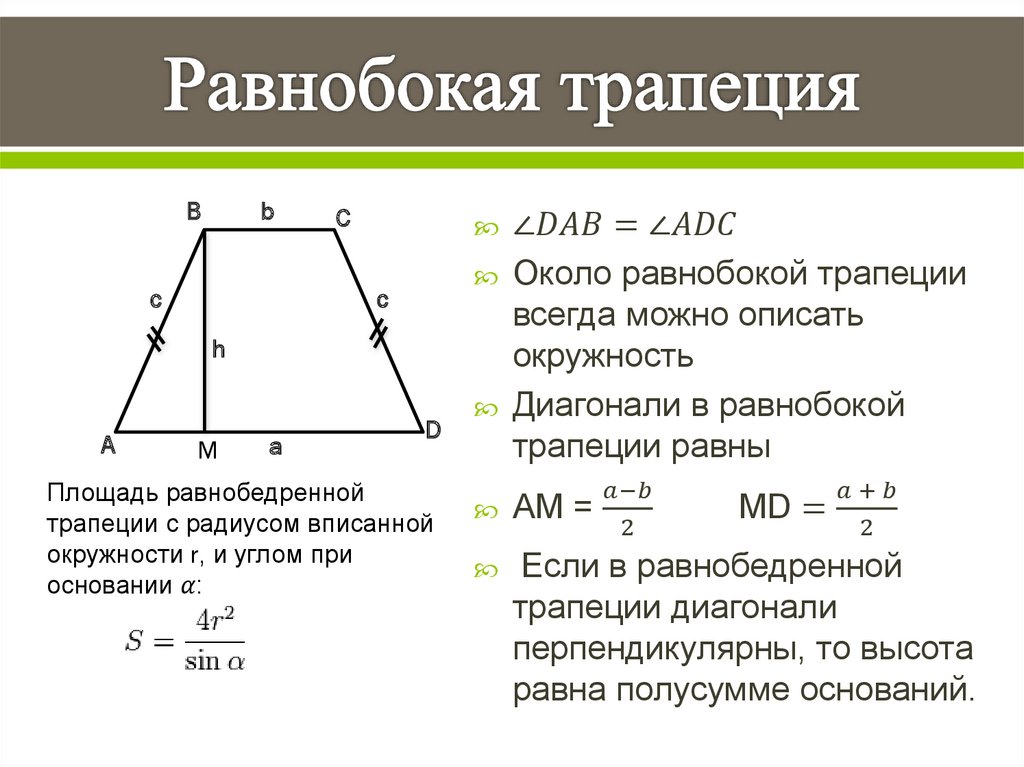
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.

Рис.1

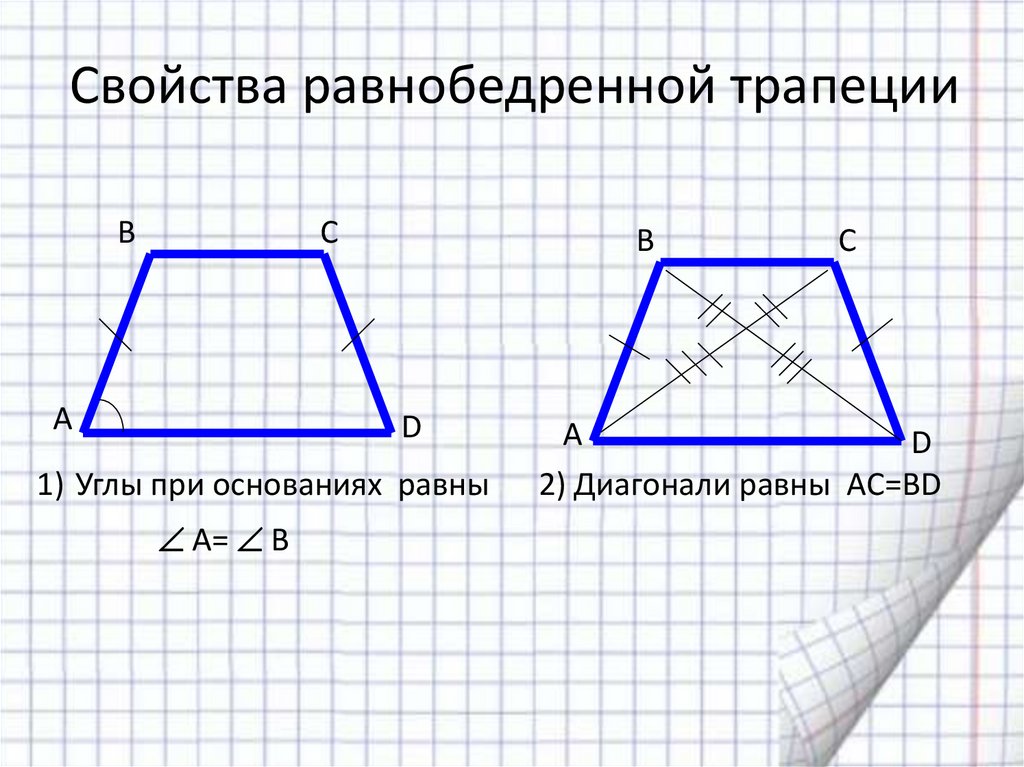
Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны:

AC = BD

3. Одинаковые углы между диагоналями и основаниями:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Основные свойства равнобедренной трапеции

1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:

AB = CD = m

3. Вокруг равнобедренной трапеции можно описать окружность

4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):

h = m

5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:

S_ABCD = h²

6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:

h² = BC · AD

7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:

AC² + BD² = AB² + CD² + 2BC · AD

8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:

HF ┴ BC, HF ┴ AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

AP =	BC + AD
	2

PD =	AD — BC
	2

10. Также смотрите свойства трапеции

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

1. Формулы длины сторон через другие стороны, высоту и угол:

a = b + 2h ctg α = b + 2c cos α

b = a — 2h ctg α = a — 2c cos α

c =	h	=	a — b
	sin α		2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d12 — c2	b =	d12 — c2	c = √d12 — ab
	b		a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b      b =	2S	— a
	h		h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

с =	S
	m sin α

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

с =	2S
	(a + b) sin α

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

1. Формула определения длины средней линии через основания, высоту и угол при основании:

m = a — h ctg α = b + h ctg α = a — √c² — h² = b + √c² — h²

2. Формула средней линии трапеции через площадь и сторону:

m =	S
	c sin α

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√4c2 — (a — b)2
	2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
	2

Диагонали равнобедренной трапеции

Диагонали равнобедренной трапеции равны:

d₁ = d₂

Формулы длины диагоналей равнобедренной трапеции:

1. Формула длины диагонали через стороны:

d₁ = √с² + ab

2. Формулы длины диагонали по теореме косинусов:

d₁ = √a² + c² — 2ac cos α

d₁ = √b² + c² — 2bc cos β

3. Формула длины диагонали через высоту и среднюю линию:

d₁ = √h² + m²

4. Формула длины диагонали через высоту и основания:

d1 =	1	√4h2 + (a + b)2
	2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√4c2 — (a — b)2
	4

2. Формула площади через стороны и угол:

S = (b + c cos α) c sin α = (a — c cos α) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
	sin α		sin β

4. Формула площади через основания и угол между основой и боковой стороной:

S =	ab	=	ab
	sin α		sin β

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = (a + b) · r = √ab·c = √ab·m

6. Формула площади через диагонали и угол между ними:

S =	d12	· sin γ	=	d12	· sin δ
	2			2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

S =	a + b	· h
	2

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где

p =	a + c + d1
	2

a — большее основание

Все таблицы и формулы

Калькулятор правильной трапеции

Создано Луцией Заборовской, доктором медицинских наук, кандидатом наук

Отзыв Габриэлы Диаз

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Что такое правильная трапеция?
• Как рассчитать наклон прямоугольной трапеции?
• Как рассчитать длину правильной трапеции?
• Другие калькуляторы, связанные с трапециями
• Часто задаваемые вопросы

Правильный калькулятор трапеций действительно правильный инструмент для вычисления всех свойств нашей любимой трапеции.

Мы покажем вам, в чем разница между «типовой» и прямоугольной трапецией , и научим вас вычислять наклон прямоугольной трапеции . Следите за текстом, чтобы узнать больше!

Какая трапеция правильная?

Прямой трапецией называется трапеция, у которой одна сторона перпендикулярна обоим основаниям . Другими словами, это означает, что такая трапеция должна содержать два прямых угла .

Это должен быть наш любимый вид трапеций — так проще считать! Это потому, что высота трапеции равна одной из ее сторон .

Не беспокойтесь — наш правильный калькулятор трапеции здесь, чтобы помочь вам со всеми необходимыми шагами. 👌 Рассчитаем:

• Трапеция правая площадь ;
• Правая трапеция наклонная сторона ;
• Трапеция правая высота ;
• Правая трапеция периметр ;
• Прямоугольная трапеция уголки ; и
• Правая трапеция Медиана — доступно в расширенном режиме .

💡 Прямоугольник также является прямой трапецией — он удовлетворяет условию, описанному выше!

Как рассчитать наклон прямоугольной трапеции? 92) }d=(a−b)2+(c2)

​

Где:

• d — наклонная (длинная) сторона трапеции;
• — более длинная база;
• b — короткая база; и
• c короткая сторона (высота трапеции).

Как рассчитать длину правильной трапеции?

Прямоугольная трапеция действительно особенная — ее высота равна длине меньшей стороны. Мы можем легко вычислить его, используя модификацию теоремы Пифагора: 92} b=d2−(a−c)2

​

Где:

• b — более короткое основание;
• d — наклонная (длинная) сторона трапеции;
• — более длинная база; и
• c короткая сторона (высота трапеции).

Доволен нашим калькулятором правильной трапеции? Ознакомьтесь со всеми другими замечательными инструментами, которые помогут вам вычислить все свойства трапеций, которые могут вам понадобиться :

• Калькулятор трапеции
• Калькулятор площади трапеции
• Калькулятор периметра трапеции
• Калькулятор стороны трапеции
• Калькулятор угла трапеции
• Калькулятор высоты трапеции
• Средняя часть трапеции
• Калькулятор равнобедренной трапеции
• Калькулятор площади равнобедренной трапеции
• Калькулятор площади правой трапеции
• Калькулятор площади неправильной трапеции

Часто задаваемые вопросы

Существует ли трапеция с одним прямым углом?

Нет, это не так.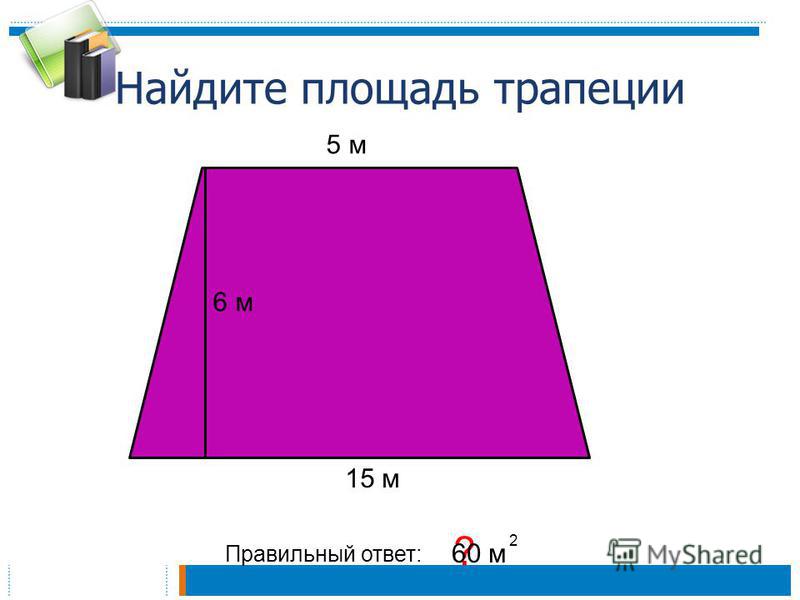 У трапеции может быть два прямых угла или не быть ни одного.

Почему так? 🤔

Два основания трапеции должны быть параллельны друг другу. Поэтому, если одна из сторон лежит под прямым углом ( перпендикулярно ) к одному из оснований, то она также должна быть перпендикулярна ко второму.

Люция Заборовска, доктор медицинских наук, кандидат наук

a (основание)

b (основание)

c (сторона/высота)

d (наклонная сторона)

Площадь (A)

Периметр (P)

Периметр (P) 30

2D Геометрия калькуляторы 📏

Площадь с прямоугольником полумесяца… 20 еще

Прапезоидной зоны.Что такое правильная трапеция?

Как найти площадь правильной трапеции

Как использовать калькулятор площади правильной трапеции

Другие калькуляторы площади трапеции

Часто задаваемые вопросы

Добро пожаловать в калькулятор площади правильной трапеции , где вы сможете вычислить площадь любой правильной трапеции в мгновение ока! 😉
Здесь мы также узнаем:

• Что такое прямая трапеция ; и
• Как найти площадь правильной трапеции сами, даже если сначала не знаете его высоты.

Начнем?

Что такое прямая трапеция?

Прямоугольная трапеция является частным случаем трапеции, четырехсторонней геометрии, по крайней мере, с одной парой противоположных сторон, параллельных друг другу. Эти параллельные стороны, также известные как основания, обозначены на изображении ниже как aaa и bbb.

В конкретном случае прямой трапеции одна из двух оставшихся сторон, ccc на рисунке, перпендикулярен параллельным сторонам aaa и bbb, образуя между ними углы 90° (прямые углы).

Как найти площадь правильной трапеции

Чтобы найти площадь правильной трапеции , используйте формулу: A = (a + b) x h/2 .

Где:

• А – Площадь трапеции;
• a и b – основания нижние и верхние; и
• h – Высота.

Это означает, что если вы знаете все эти измерения, вы сможете вычислить площадь вашей правой трапеции напрямую.

Но что, если вы не знаете высоту h ? Сможете ли вы еще вычислить площадь? Вот тут и приходит на помощь старая добрая тригонометрия!

Глядя на изображение, мы видим прямоугольный треугольник, образующийся из высоты h , разности оснований (a - b) и сбоку d .

Отсюда, если знаете:

• две стороны (a - b) и d ; или
• Одна сторона и один угол прямоугольного треугольника, все готово!

Если вы знаете две стороны , вычисление h вращается вокруг теоремы Пифагора как:

• h = √(d² - (a - b)²)

С другой стороны, если у вас есть одна сторона и один угол , вы можете получить значение h с помощью функции арксинуса (обратная синусоидальной) как:

• h = arcsin(δ) * d

или. ..

• h = arcsin(γ - π/2) * d

💡 Вы можете узнать больше о тригонометрической функции арксинуса с помощью нашего калькулятора арксинуса. Чтобы узнать о других тригонометрических функциях, воспользуйтесь нашим калькулятором тригонометрии!

Как пользоваться калькулятором площади правильной трапеции

Чтобы использовать калькулятор площади правой трапеции:

1. Введите основания a и b . Например, предположим, что a = 10 и b = 6 .
2. Введите значение высоты h . В нашем примере предположим, что ч = 4 .
3. Калькулятор отобразит результат для площади в последней строке. Для нашего расчета мы получаем A = 32 . Вот и все! 😀

💡 Не знаете значение высоты h ? Нажмите кнопку расширенного режима , чтобы получить значение площади путем ввода углов и наклонной стороны.

Другие калькуляторы трапеций

Теперь, когда вы научились вычислять площадь правильной трапеции, почему бы не прочитать о площади неправильной трапеции или не расширить свои знания о трапециях с помощью нашего калькулятора трапеций.

Чтобы узнать о конкретных темах, касающихся трапеций, мы рекомендуем другие наши инструменты:

• Калькулятор трапеций
• Калькулятор площади трапеции
• Калькулятор периметра трапеции
• Калькулятор стороны трапеции
• Калькулятор угла трапеции
• Калькулятор высоты трапеции
• Средняя часть калькулятора трапеций
• Калькулятор равнобедренной трапеции
• Калькулятор площади равнобедренной трапеции
• Калькулятор правой трапеции
• Калькулятор площади неправильной трапеции

Часто задаваемые вопросы

Может ли трапеция иметь ровно один прямой угол?

Нет, трапеция не может иметь только один прямой угол.