Основы трапеции: Трапеция — урок. Геометрия, 8 класс.

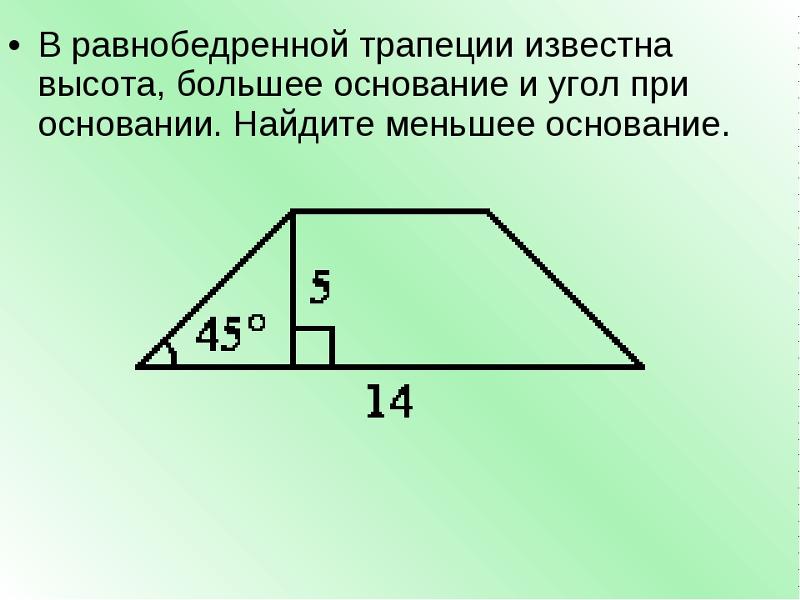
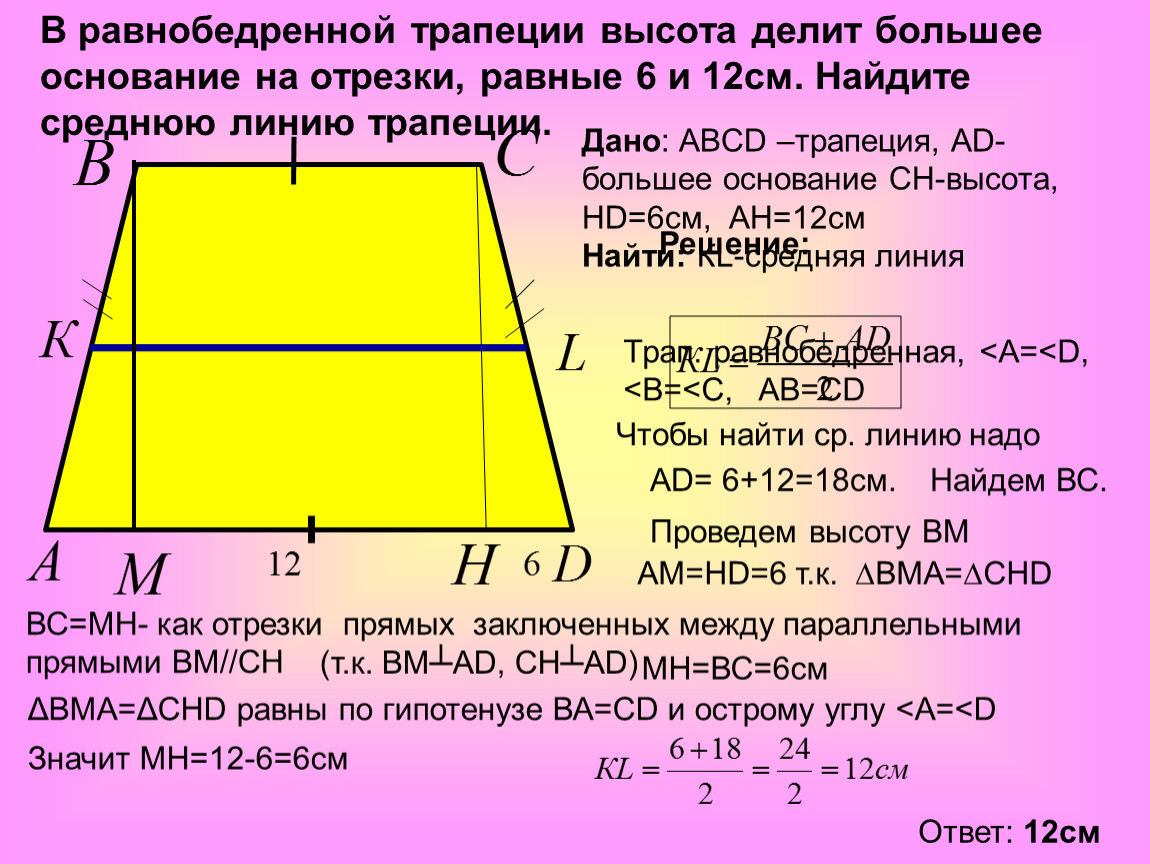
Трапеция. Формулы, признаки и свойства трапеции

Навигация по странице: Определение трапеции Элементы трапеции Виды трапеций Основные свойства трапеции Стороны трапеции Средняя линия трапеции Высота трапеции Диагонали трапеции Площадь трапеции Периметр трапеции Окружность описанная вокруг трапеции Окружность вписанная в трапецию Другие отрезки трапеции

Определение.

Трапеция — это четыреугольник у котрого две стороны паралельны, а две другие стороны не паралельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четыреугольник у которого одна пара противоположных сторон паралельна и стороны не равны между собой.

Элементы трапеции:

• Основы трапеции — параллельные стороны
• Боковые стороны — две другие строрны
• Средняя линия — отрезок, соединяющий середины боковых сторон.

Виды трапеций:

• Равнобедренная трапеция — трапеция у которой боковые стороны равны
• Прямоугольная трапеция — трапеция у которой одна из боковых сторон перпендикулярна основам

Рис. 1		Рис.2

Основные свойства трапеции

1. В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

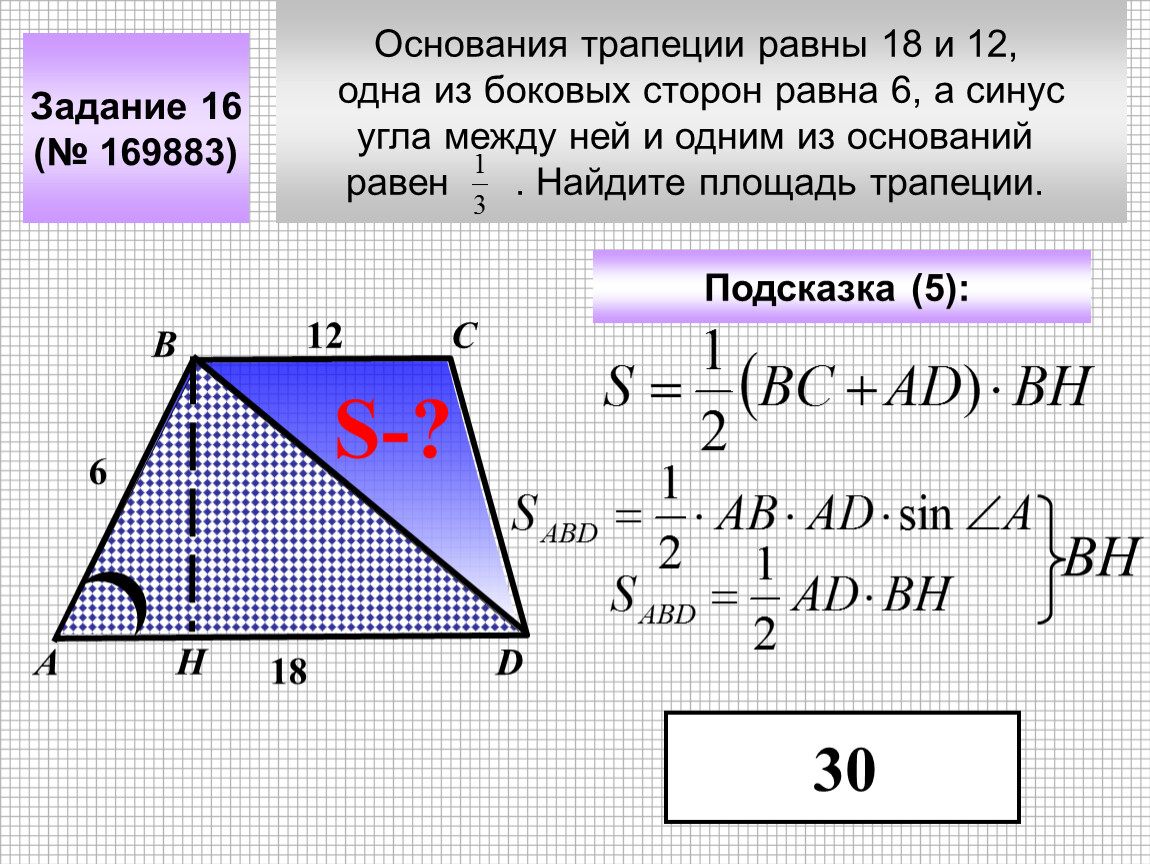
3. Средняя линия трапеции паралельна основаниям и равна их полусумме:

m =	a + b
	2

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины как сотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через середнюю линию и другую основу:

a = 2m — b

b = 2m — a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a — h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a — c·cos α — d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Средняя линия трапеции

Определение.

Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

m =	a + b
	2

2. Формула определения длины средней линии через площадь и высоту:

m =	S
	h

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d1 d2	=	sin δ ·	d1 d2
		a + b			a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d1 d2	=	sin δ ·	d1 d2
		2m			2m

4. Формула высоты трапеции через площадь и длины оснований:

h =	2S
	a + b

5.

Формула высоты трапеции через площадь и длину средней линии:

h =	2S
	m

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² — 2ad·cos β

d₂ = √a² + c² — 2ac·cos β

2. Формулы диагоналей через четыре стороны:

d1 =	√	d 2 + ab —	a(d 2 — c2)	d2 =	√	c2 + ab —	a(c2 — d 2)
			a — b				a — b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a — h · ctg β)

2 = √h² + (b + h · ctg α)²

d₂ = √h² + (a — h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab — d₂²

d₂ = √c² + d ² + 2ab — d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

S =	(a + b)	· h
	2

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через через диагонали и угол между ними:

S =	d1d2	· sin γ	=	d1d 2	· sin δ
	2			2

4. Формула площади через четыре стороны:

S =	a + b	√	c2 —	(	(a — b)2 + c2 — d 2	)	2
	2				2(a — b)

5. Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
	|a — b|

где

p =	a + b + c + d	— полупериметр трапеции.
	2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где

p =	a + c + d1
	2

a — большее основание

Окружность вписанная в трапецию

В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

r =	h
	2

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Трапеция, ее свойства, формулы площади, высоты, сторон

Трапеция, ее свойства, формулы площади, высоты, сторон.

 

Поделиться в:

 

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

 

Трапеция (понятие, определение)

Видеоурок “Трапеция”

Виды трапеций

Элементы трапеции: основания, боковые стороны, средняя линия и высота

Свойства трапеции

Свойства равнобедренной трапеции

Формулы трапеции

 

Трапеция (понятие, определение):

Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.

Рис. 1. Трапеция

Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

@ https://youtu.be/Q4EpXexoMrM

 

 

Виды трапеций:

Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.

Рис. 2. Равнобедренная трапеция

Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.

Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.

Рис. 3. Прямоугольная трапеция

 

Элементы трапеции: основания, боковые стороны, средняя линия и высота:

Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.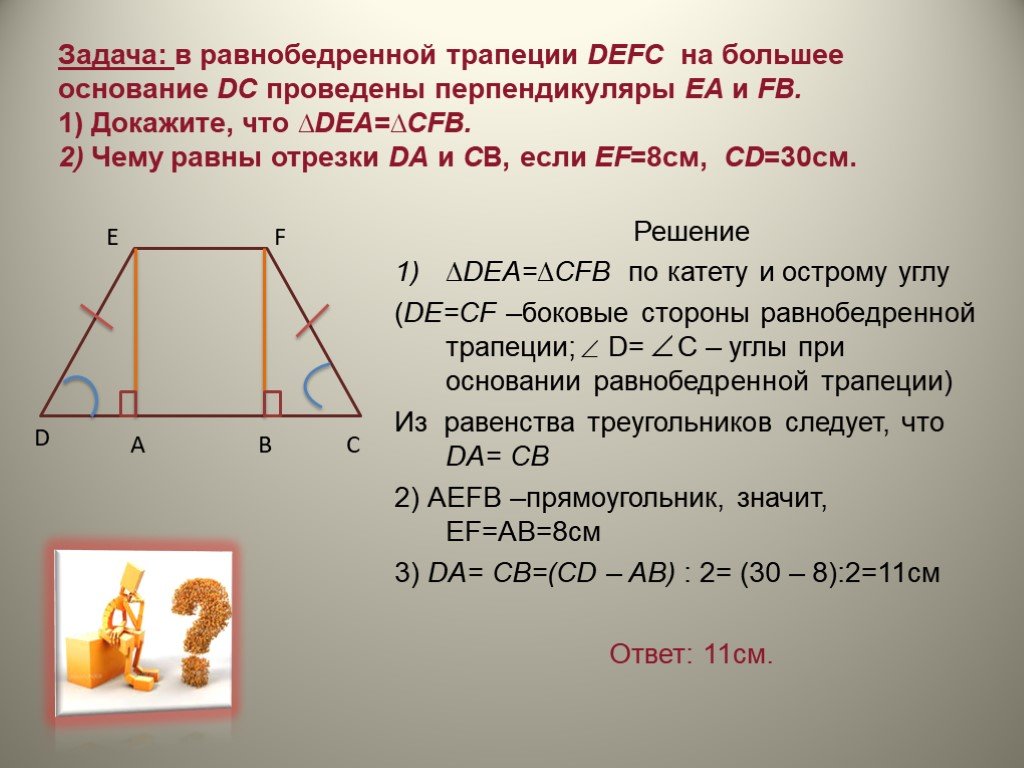

Рис. 4. Трапеция 

AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.

AD – большее основание трапеции, BC – меньшее основание трапеции.

Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.

Рис. 5. Трапеция и срединная линия

Расстояние между основаниями трапеции называется высотой трапеции.

Рис. 6. Трапеция

Высота трапеции (h) определяется формулой:

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

 

Свойства трапеции:

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Рис. 7. Трапеция и срединная линия

MN || BC, MN || AD,

l = (a + b) / 2 

2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии. 

Рис. 8. Трапеция

MN = (b – a) / 2 

3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .

Сумма углов, прилежащих к боковой стороне трапеции, равна  180° . 

Рис. 9. Трапеция 

4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

Рис. 9. Трапеция

5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

 Рис. 10. Трапеция

AB = BK

6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.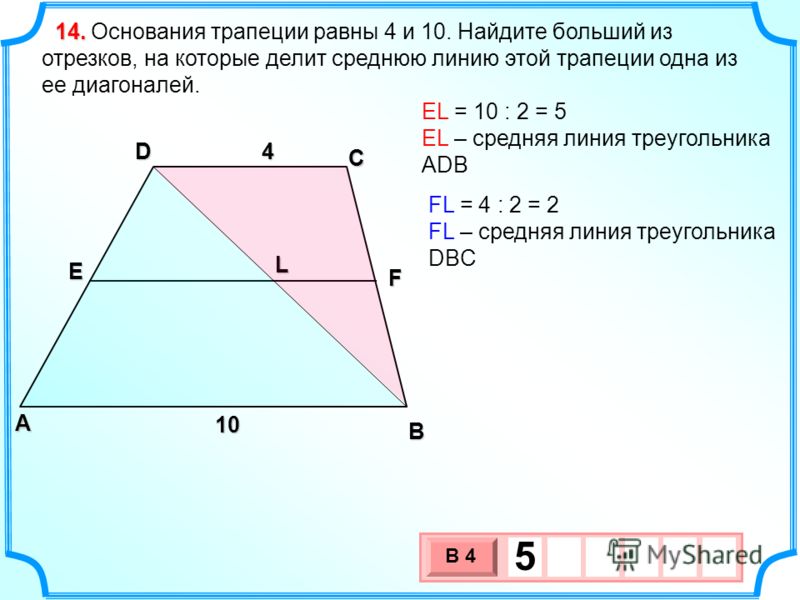

Рис. 11. Трапеция

∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2 

7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.

Рис. 12. Трапеция

AB + CD = AD + BC 

В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

Рис. 13. Трапеция 

Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).

Рис. 14. Трапеция

MN = (AB + CD) / 2,

MN = (AD + BC) / 2

8. Диагонали трапеции делят ее на 4 треугольника.

Два из них, прилежащие к основаниям, подобны.

Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.

Рис. 15. Трапеция

Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции.  k = AD / BC. Отношение площадей этих подобных треугольников есть k².

Треугольники ABO и CDO имеют одинаковую площадь.

9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.

Рис. 16. Трапеция

BC : AD = OC : AO = OB : DO

10. Диагонали трапеции d₁и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c ² + d ²    

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.

Рис. 17. Трапеция

AK = KB, AM = MC, BN = ND, CL = LD,

KL – средняя линия

Рис. 17. Трапеция

AK = KB, AM = MC, BN = ND, CL = LD,

KL – средняя линия, UV – отрезок, который соединяет основания трапеции

12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:

где b – большее основание трапеции, a – меньшее основание трапеции, S₁ и S₂ – площади образованных трапеций, в результате разделения средней линией.

Рис. 18. Трапеция

S₁ – площадь трапеции MBCN,

S₂ – площадь трапеции AMND

 

Свойства равнобедренной трапеции:

1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.

2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.

3. Углы при любом основании равнобедренной трапеции равны.

4. Сумма противоположных углов равнобедренной трапеции равна 180°.

5. Длины диагоналей равнобедренной трапеции равны.

6. Вокруг равнобедренной трапеции можно описать окружность.

7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.

 

Формулы трапеции:

Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d₁ и d₂ – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.

 

Формулы для определения сторон трапеции:

Через среднюю линию и одно из оснований трапеции:

a = 2m – b

b = 2m – a

Через высоту и углы при нижнем основании трапеции:

a = b + h · (ctg α + ctg β)

b = a – h · (ctg α + ctg β)

Через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a – c·cos α – d·cos β

Через высоту и углы при нижнем основании трапеции:

 

Формулы для определения средней линии трапеции:

Через длины оснований трапеции:

Через площадь и высоту трапеции:

 

Формулы для определения высоты трапеции:

Через сторону и прилегающий угол при нижнем основании трапеции:

h = c·sin α = d·sin β

Через диагонали трапеции и углы между ними:

Через диагонали трапеции, углы между ними и среднюю линию трапеции:

Через площадь и длины оснований трапеции:

Через площадь и длину средней линии трапеции:

 

Формула для определения периметра трапеции:

P = a + b + c + d

 

Формулы для определения площади трапеции:

Через основания и высоту трапеции:

Через среднюю линию и высоту трапеции:

S = m · h

Через диагонали трапеции и угол между ними:

Через все стороны трапеции:

С помощью формулы Герона для трапеции:

 

Как называется объемная трапеция?

Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.

В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.

 

Квадрат

Овал

Полукруг

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Трапеция

Тупой угол

Шестиугольник

 

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Видео https://youtu.be/Q4EpXexoMrM

 

 

Коэффициент востребованности 6 680

Площадь трапеции — определение, формулы, вывод, примеры и свойства

Площадь трапеции — это область, покрытая трапецией в двумерной плоскости. Это пространство, заключенное в двумерную геометрию и измеренное в квадратных единицах. Трапеция — это двумерная фигура, относящаяся к категории четырехугольников. Подобно другим геометрическим фигурам, она также имеет свои свойства и формулы, основанные на площади и периметре. Следовательно, площадь формулы трапеции объясняется в статье вместе с ее выводом и примерами, чтобы вы лучше поняли.

Содержание: Определение Формула Производная Как рассчитать? Видео урок Концепция трапеции Свойства Приложения Решенные примеры Практические вопросы Часто задаваемые вопросы

Что такое площадь трапеции?

Трапеция — это четырехугольник, который определяется как фигура с четырьмя сторонами и одним набором параллельных сторон. Таким образом, площадь трапеции — это область, покрытая этими четырьмя сторонами. Площадь трапеции в основном зависит от длины параллельных сторон и высоты трапеции. Измеряется в квадратных единицах. Давайте посмотрим формулу, чтобы найти площадь любой трапеции.

Площадь трапеции Формула

Площадь трапеции можно рассчитать по следующей формуле:

Площадь = (1/2) h (a+b)

где,

• а и b — длины параллельных сторон/оснований трапеции
• h — высота или расстояние между параллельными сторонами.

Из рисунка площадь трапеции = 1/2 (AB + DC).h

Периметр Трапеции

Формула периметра трапеции определяется по формуле:

Периметр = сумма всех сторон = AB + BC + CD + DA

Вывод площади трапеции

Ниже приведен вывод для вычисления площади трапеции:

Площадь трапеции равна сумме площадей двух треугольников и площади прямоугольника.

Мы знаем, что

площадь трапеции = площадь треугольника 1 + площадь прямоугольника + площадь треугольника 2.

Значит,

A = (ah/2) + b ₁ h + (ch/2) ​​

A = (ah + 2b ₁ h + ch)/2

Упрощение уравнения, перестановка членов и результат разложения на множители:

А = h/2[b ₁ + (a + b ₁ + c)] ….(i)

Если предположить, что большее основание трапеции равно b ₂ , то

b ₂ = a + b ₁ + c ….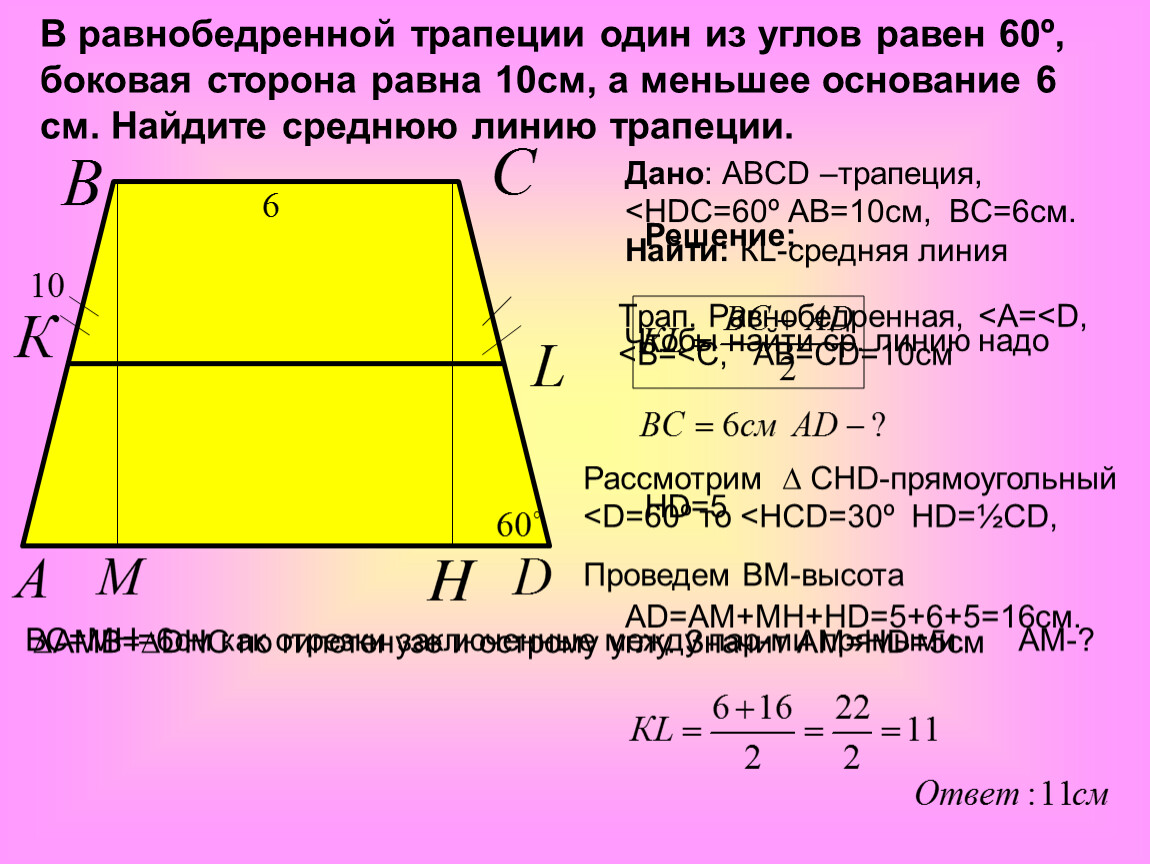 .(ii)

Подставив (ii) в уравнение (i),

А = ч/2(б ₁ + б ₂ )

Следовательно, площадь трапеции с основаниями b ₁ , b ₂  и высотой h равна;

А = h/2(b ₁ +b ₂ )

Как рассчитать площадь трапеции?

Чтобы найти площадь трапеции, выполните следующие шаги:

• Шаг 1: Найдите размеры данной трапеции, т.е. длину параллельных сторон и длину высоты.
• Шаг 2: Добавьте длины параллельных сторон
• Шаг 3: Умножьте сумму параллельных сторон на высоту трапеции
• Шаг 4: Теперь умножьте рассчитанное выше значение на 1/2, чтобы получить окончательный ответ

Полученное значение на шаге 4 является площадью заданной трапеции.

Видеоурок по площади трапеции

Базовая концепция трапеции

1. Пара параллельных сторон называется основаниями, а непараллельные стороны называются катетами трапеции
2. Отрезок, соединяющий середины непараллельных сторон трапеции, называется серединой
3. Проверьте выше различные типы фигур трапеции, где стрелка представляет собой параллельную сторону. На всех трех рисунках две стороны параллельны друг другу, тогда как две другие стороны не параллельны
4. Если мы проведем отрезок между двумя непараллельными сторонами, из середины обеих сторон,  трапеция будет разделена на две неравные части.
5. Вы должны знать о равнобедренных треугольниках, где две стороны треугольника равны, и угол, лежащий против равных сторон, также равен. Точно так же у нас есть фигура, которая обозначена как Равнобедренная Трапеция , где две непараллельные стороны равны и образуют равные углы при одном из оснований. Вы можете увидеть пример этого на третьем рисунке, приведенном выше.

Свойства трапеции

Здесь мы узнаем еще о некоторых свойствах трапеции, которую также называют трапецией. Трапеция обладает следующими свойствами:

1. Как и у других четырехугольников, сумма всех четырех углов трапеции равна 360°
2. Трапеция имеет две параллельные стороны и две непараллельные стороны
3. Диагонали правильной трапеции делят друг друга пополам
4. Длина среднего отрезка равна половине суммы параллельных оснований трапеции
5. Две пары смежных углов трапеции, образованных между параллельными сторонами и одной из непараллельных сторон, в сумме дают 180 градусов

Применение трапеции

Концепция широко используется в различных физических вычислениях и других математических вычислениях. Это основа для получения уравнений движения, как описано в 9-м научном учебнике CBSE. Сочетание физических уравнений и математических расчетов очень хорошо объяснено, чтобы прояснить уровень понимания подающего надежды инженерного ума.

Связанные статьи

Решенные примеры на площади трапеции

Вопрос 1: Найдите площадь трапеции, длина параллельных сторон которой равна 4 см и 6 см соответственно, а высота равна 3 см.

Решение: Дано,

длина параллельных сторон трапеции;

а = 4см

б = 6см

Высота трапеции, h = 3см

Следовательно,

площадь трапеции = 1/2 (a+b).h

= 1/2 (4 + 6) х 3

= 15 кв см.

Q.2: Какова площадь трапеции, если основания равны 12 см и 20 см соответственно, а расстояние между двумя параллельными сторонами равно 10 см?

Решение: Дано,

а = 12 см

б = 20 см

расстояние между двумя параллельными сторонами, h = 10 см

Площадь трапеции = 1/2 (12 + 20) 10

= 160 кв. см

Практические вопросы

1. Найдите площадь трапеции, длина параллельных сторон которой равна 12 см и 6 см соответственно, а расстояние между параллельными сторонами равно 5 см.
2. Если площадь трапеции 728 см ² . Найдите высоту трапеции такой, что длины ее параллельных сторон равны 16 см и 7 см соответственно.
3. Площадь трапеции 384 см². Если 3:5, то это отношение длины его параллельных сторон к перпендикулярному расстоянию между ними равно 12 см. Найдите длину каждой из параллельных сторон.

Для полного понимания и прояснения концепции нужно просмотреть практические рабочие листы в BYJU’S, чтобы проверить свои навыки работы с концепцией и проверить обучение.

Часто задаваемые вопросы о площади трапеции

Q1

Какова формула площади трапеции?

Формула для расчета площади трапеции:
Площадь = ½ x Сумма параллельных сторон x Расстояние между параллельными сторонами

Q2

Какие формулы для площади и периметра трапеции?

Площадь трапеции = ½ x (a+b) x h
Периметр трапеции = a+b+c+d
Где a, b, c и d — длины сторон трапеции
А h — расстояние между две параллельные стороны, т. е. а и b.

Q3

Каковы свойства трапеции?

Трапеция имеет 4 неравные стороны: две параллельные и две непараллельные стороны
Сумма всех внутренних углов равна 360 градусов
Диагонали делят друг друга пополам

Q4

Как найти площадь трапеции?

Площадь трапеции зависит от ее параллельных сторон и расстояния между параллельными сторонами.
Если нам известны длины параллельных сторон и расстояние между ними, то мы легко можем найти площадь трапеции.

Q5

Как определить форму трапеции?

Трапеция представляет собой плоскую форму или двухмерную форму с 4 прямыми сторонами. Он также известен как трапеция, которая содержит две параллельные стороны (обычно называемые основаниями) и две непараллельные стороны, называемые катетами.

Q6

Сколько углов у трапеции?

Трапеция содержит четыре угла, так как является четырехугольником.

Q7

Является ли трапеция четырехугольником?

Да, трапеция — четырехугольник, так как у нее четыре стороны.

Q8

Чему равна сумма внутренних углов трапеции?

Сумма внутренних углов трапеции равна 360 градусов (360°).

Трапеция — Недвижимость | Формулы | Определение

ОБЕЩАНИЕ НА 30 ДНЕЙ | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*

*T&C Применить

LearnPracticeDownload

Трапеция представляет собой четырехугольник, в котором одна пара противоположных сторон параллельна. Давайте узнаем больше об определении трапеции, свойствах трапеции, различных типах трапеций, углах трапеции и диагоналях трапеции, а также некоторых примерах трапеций.

1.	Что такое трапеция в математике?
2.	Типы трапеций
3.	Свойства трапеции
4.	Формулы трапеции
5.	Часто задаваемые вопросы о трапеции

Что такое трапеция в математике?

Трапеция представляет собой двумерный четырехугольник с одной парой параллельных сторон. Параллельные стороны трапеции называются «основаниями», а непараллельные стороны известны как «ножки» трапеции.

Трапеция Определение

Трапеция представляет собой замкнутую плоскую фигуру, имеющую четыре стороны, в которой одна пара противоположных сторон параллельна. Обратите внимание на фигуру трапеции, приведенную ниже, которая показывает трапецию WZYX, в которой WZ параллельна XY, и они являются основаниями, а WX и ZY являются сторонами трапеции.

Типы трапеций

Существуют в основном три различных типа трапеций, которые приведены ниже:

• Равнобедренная трапеция
• Лестничная трапеция
• Правая трапеция

Трапеции классифицируются на основе длины ножек или измерения их углов. Определение каждого типа трапеции вместе с ее формой дано ниже.

Свойства трапеции

У каждого четырехугольника есть свои свойства, которые делают его узнаваемым и отличным от остальных. Эти свойства дают больше информации о геометрической конструкции формы. Основные свойства трапеции перечислены ниже:

• Трапеция — это двумерная фигура.
• Основания трапеции параллельны друг другу.
• Диагонали трапеции всегда пересекаются.
• Сумма смежных внутренних углов равна 180°.
• Сумма всех внутренних углов трапеции всегда равна 360°.

Углы трапеции

В трапеции 4 внутренних угла, сумма которых составляет 360°, а сумма смежных внутренних углов составляет 180°.

Диагонали трапеции

Поскольку трапеция является четырехугольником, у нее 2 диагонали, и обе они пересекаются.

Формулы трапеции

Формулы трапеции в основном связаны с площадью трапеции и периметром трапеции.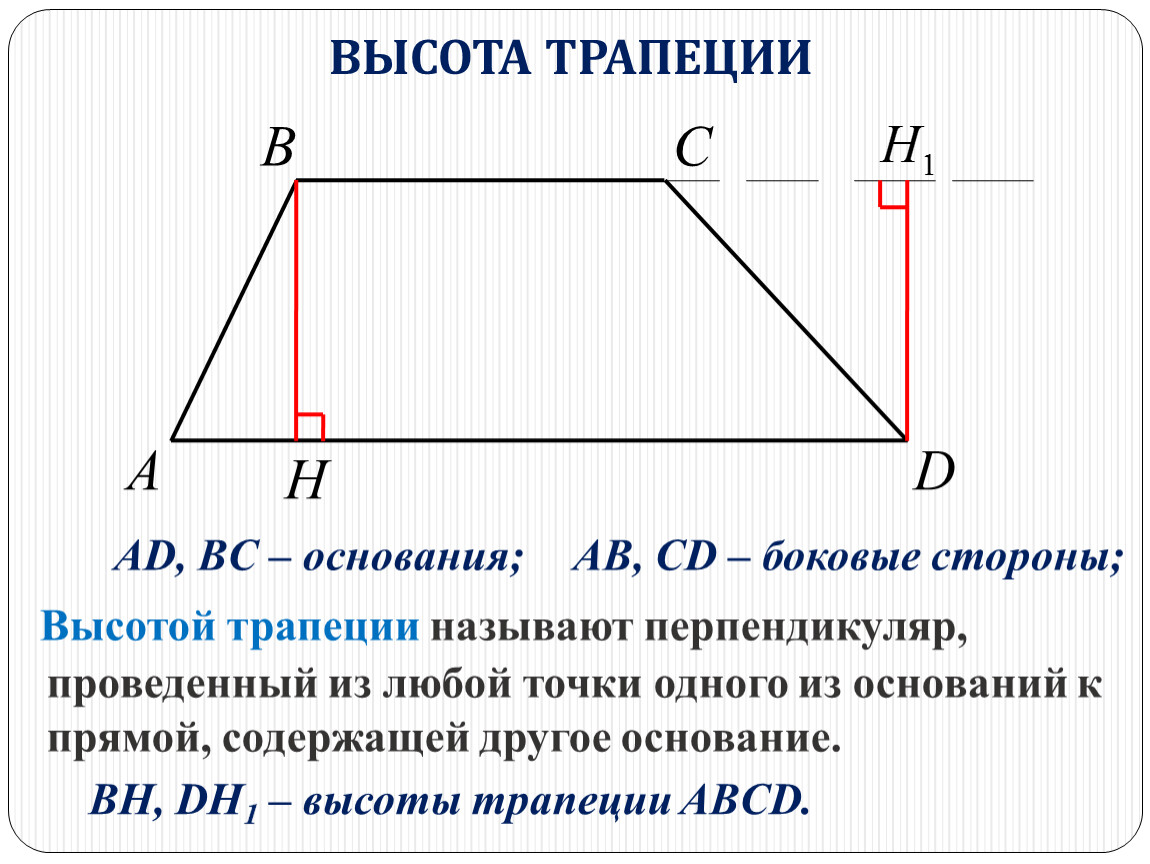 Возьмем в качестве примера диаграмму трапеции, в которой параллельные стороны обозначены как «a» и «b» соответственно, а высота (высота) обозначена как «h». Обратите внимание на трапецию ABCD, приведенную ниже, чтобы понять формулы трапеции, приведенные после этого.

• Формула, используемая для нахождения площади трапеции , выражается следующим образом. Площадь трапеции = 1/2 × сумма параллельных сторон × высота. На этом рисунке это можно записать как Площадь трапеции = 1/2 × (a + b) × h, где «a» и «b» — параллельные стороны, а «h» — высота трапеции.
• Периметр трапеции можно вычислить, сложив длины всех 4 сторон. Это означает, что формула, которая используется для нахождения периметра трапеции, выражается следующим образом. Периметр трапеции = Сумма всех 4 сторон . На этом рисунке это можно записать как Периметр трапеции ABCD = AB + BC + CD + DA.

☛ Статьи по теме

Посмотрите эти интересные статьи, связанные с концепцией формы трапеции в геометрии.

• Четырехугольники
• Трапеция
• Площадь трапеции
• Формула трапеции
• Калькулятор площади трапеции
• Равнобедренная трапеция

 

Примеры трапеций

1. Пример 1: Укажите истинное или ложное значение относительно свойств трапеции:

   а.) Все квадраты являются трапециями.

   б.) Трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна.

   Решение:

   а.) Верно, что все квадраты являются трапециями, потому что у квадрата противоположные стороны параллельны, поэтому он удовлетворяет этому свойству трапеции.

   б.) Верно, трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна.

2. Пример 2: Найдите четвертый угол прямой трапеции, если один из заданных углов равен 60°.

   Решение: Как известно, в прямой трапеции 2 прямых угла и сумма всех внутренних углов трапеции всегда равна 360°.

   Итак, если один из заданных углов равен 60°, пусть недостающий угол равен x°. Четвертый угол можно рассчитать как x° + 90° + 90° + 60° = 360°.
   ⇒ х° = 360° — (90° + 90° + 60°) = 120°. Следовательно, мера четвертого угла равна 120°.

3. Пример 3: Найдите длину четвертой стороны трапеции, если остальные три стороны имеют длину 10 единиц, 12 единиц и 7 единиц, а периметр равен 40 единицам.

   Решение: Как известно, периметр трапеции равен сумме всех ее сторон. Пусть недостающая длина стороны будет «a». Таким образом, периметр равен 40 = 10 + 12 + 7 + а.
   ⇒ а = 40 — (10 + 12 + 7) = 11 единиц. Следовательно, длина четвертой стороны равна 11 единицам.

перейти к слайдуперейти к слайдуперейти к слайду

Хотите создать прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

Практические вопросы по трапеции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о трапеции

Что такое форма трапеции?

Трапеция — это двумерный четырехугольник с одной парой параллельных сторон. Параллельные стороны трапеции известны как «основания», а непараллельные стороны называются катетами трапеции. Он выглядит как треугольник, который срезан сверху.

Как найти площадь трапеции?

Площадь трапеции можно рассчитать по формуле Площадь трапеции = 1/2 × Сумма параллельных сторон × высота. Это означает, что если мы знаем длину параллельных сторон и высоту, мы можем найти площадь трапеции.

Является ли трапеция четырехугольником?

Да, трапеция — четырехугольник. У него четыре стороны, четыре вершины и четыре угла. Сумма всех четырех внутренних углов трапеции равна 360 градусов.

Есть ли у трапеции параллельные стороны?

Да, у трапеции одна пара параллельных сторон. Эти параллельные стороны называются основаниями трапеции.

Может ли трапеция иметь прямой угол?

Да, трапеция может иметь прямой угол. Трапеция с парой прямых углов называется прямой трапецией.

Каковы свойства трапеции?

Характеристики трапеции приведены ниже:

• Трапеция представляет собой двумерную форму и относится к категории четырехугольников.
• В трапеции есть одна пара параллельных сторон, и эти стороны называются основаниями.
• У трапеции 2 диагонали всегда пересекаются.
• Сумма смежных внутренних углов трапеции равна 180°.
• Сумма внутренних углов трапеции всегда равна 360°.

Какая формула площади трапеции?

Формула, которая используется для нахождения площади трапеции, выражается как Площадь трапеции = 1/2 × Сумма параллельных сторон × высота.

Каковы свойства равнобедренной трапеции?

Равнобедренная трапеция – это трапеция, у которой катеты, то есть непараллельные стороны, равны между собой.

В чем разница между трапецией и трапецией?

Трапеция также известна как трапеция. Они относятся к четырехстороннему многоугольнику, имеющему одну пару параллельных сторон и одну пару непараллельных сторон.

Сколько составляют углы трапеции?

В трапеции 4 внутренних угла, сумма которых составляет 360°, а сумма смежных внутренних углов составляет 180°.