Как понять круговые примеры: Математика 2 класс: что такое круговые примеры?

Составь и реши круговые примеры

Решение:

Шаг 1: Вычислим первый пример: 12-5+8 = 15, полученное число поставим в пустой квадратик следующего примера:

Шаг 2: Вычислим следующий пример: 15+2-9 = 8, полученную 8 подставим в следующий пример:

Шаг 3: Вычислим 8+10-4=14, и подставим 14 в следующий пустой квадратик.

Шаг 4: по аналогии вычислим остальные примеры и подставим в пустые квадратики:

Шаг 5:

Шаг 6:

Шаг 7:

Шаг 8: вычислим последний пример: 16+3-7 = 12 — это соответствует первому элементу в первом примере, значит, мы все решили правильно.

Как решать круговые примеры

Современная математика для школьников младших классов включает в себя основы алгебры и геометрии. Не зря от родителей первоклашек требуют, чтобы они обучили своих детей навыкам устного счета до 10, а также научили их классифицировать предметы по признакам.

Сегодняшние учебники для 1 и 2 классов заполнены такими заданиями, над которыми ломают головы папы и мамы учеников младших классов. Однако у самих учеников и задачи не вызывают затруднений, поскольку наряду с обычными математическими действиями на уроках математики обучают и началам математической логики.

Так называемые «круговые примеры» относятся именно к таким заданиям, в которых надо не просто складывать, вычитать и умножать, но и выстроить логический ряд. Детям задается некоторое количество примеров, которые они должны выполнить в правильной последовательности.Правила круговых примеров таковы.

Все примеры даются вперемешку. Ответ одного примера служит началом для последующего. Из общего количества примеров задания выбираются именно таким образом и выстраиваются в цепочку (столбик).

Не получив правильного результата, невозможно решить следующий пример и правильно составить цепочку. Ответ последнего примера является началом первого, что и дает название «круговые примеры».

Например: 7+4 5+8 11-6 13-5Решать следует: 7+4=11 11-6=5 5+8=13 13-5=7, ответ каждого примера является началом для последующего, что и составляет цепочку или круг.

Круговые примеры решаются как устно, так и письменно. Детям нравятся задания такого рода, особенно если их приходится решать на время. Поэтому очень часто при решении круговых примеров учителя прибегают к игровой форме обучения. Особенно в младших классах.

Сказочные герои народных сказок или мультфильмов задают примеры и решают их вместе со школьниками. Как правило, круговые примеры в младших классах содержат простейшие действия на сложение и вычитание однозначных чисел. Однако впоследствии круговые примеры могут содержать несколько действий на сложение, вычитание, деление и умножение двух- и трехзначных чисел.

Мои разработки > Математика > 1 класс > Решаем круговые примеры

21-04-2016 21:58:14 Guest 16-3+5=

09-01-2014 16:11:36 Nadej СПАСИБО!

14-10-2013 20:22:09 Вера СПАСИБО!!!

20-03-2013 10:45:36 Наталья круто!

03-02-2013 14:00:39 эвелина да будет о

02-02-2013 00:02:29 Guest

17-11-2012 16:40:07 Guest Спасибо большое за разъяснения!!!

14-10-2012 18:07:13 Guest что такое круговые примеры?

31-01-2012 14:36:06 валерия

25-01-2012 22:42:05 Сергей. Крым. Евпатория Спасибо. Все понятно.

16-01-2012 19:38:29 Надежда Спасибо  большое,Карина  Владимировна.Видимо,  вы  очень  одержимый  человек  и  творческий.

20-12-2011 20:41:46 Guest а где примеры

13-10-2011 10:51:52 анечка спс большое!!!!!!!!!!!!!!!!!!!!!!!!ХД

21-01-2011 23:16:07 гардения Спасибо! Вы умница!

02-11-2010 19:15:34 Татьяна Очень благодарна! Большое спасибо!

10-10-2010 08:15:18 Guest 6+6

22-08-2010 23:40:46 Алиса Отлично!  Молодцы! nlk 90671

11-08-2010 15:18:47 оксана анатольевна Большое Вам спасибо. Не все ещё умеют создавать такие интересные презентации. Я знаю, сколько уходит сил и времени на них, поэтому низкий поклон вам за бескорыстие. Здоровья и счастья! МОУ СОШ11, г. Сургут

10-08-2010 13:59:26 Natalja Очень просто и здорово1 спасибо!

26-04-2010 20:41:03 Анжелика 9

21-02-2010 20:58:34 buss galina

Что такое круговые примеры? Математика 2 класс написано решите круговые…

Примеры подбираются так, чтобы число, получаемое в результате одного из них, являлось началом другого. Ответ последнего примера совпадает с началом первого. 6+6=12, 12-5=7, 7+4=11, 11-3=8, 8+6=14, 14-5=9, 9+4=13, 13-7=6.

это примеры от которых потом голова болит! кто такие примеры придумал?

6+6=12 12-5=8 и так дальще

какой идиот этот термин придумал и какая от этого польза для изучения математики?

Первые пылесосы появились в самом конце XIX века. По устройству они напоминали шприц — уборщица тянула за ручку и пыль втягивалась в емкость пылесоса. Эта конструкция не привела хозяек в восторг — новейший прибор был тяжел и малоэффективен. Через несколько лет был изобретен первый электрический пылесос с 30-метровым шлангом, который перевозился на запряженной двумя лошадьми телеге. Один из первых пылесосов — Elmo производства компании «Сименс», 1906 г. Но инженерная мысль на нем не остановилась, и постепенно пылесос стал незаменимым помощником в хозяйстве. Сегодня, через сто с лишним лет после изобретения первого агрегата для сбора пыли, его «потомки» есть почти в каждом доме. Обойтись без пылесоса невозможно! 1. Принцип работы пылесоса Принцип работы пылесоса достаточно прост. По большому счету, пылесос состоит из трех основных узлов. Это электродвигатель, насос и фильтр. Работа заключается том, что электродвигатель с помощью насоса создает разрежение воздуха под щеткой пылесоса. За счет этого, пыль и грязь засасываются в пылесос, а затем воздух очищается от них фильтром. Вот, собственно, и все. Существующие, в настоящее время, различные виды пылесосов, являются лишь вариациями на эту тему. В них могут использоваться различные типы фильтров, различные насосы, но суть остается одна и та же. Важнейшим элементом пылесоса является его фильтр. Без эффективной фильтрации, пылесос будет просто подымать пыль с пола и выбрасывать его вновь в воздух. По современным меркам, задержка даже 99% пыли не обеспечивает необходимого уровня чистоты воздуха, поскольку именно в оставшемся 1% пыли содержатся бактерии, вирусы и аллергены. Поэтому, качественным уровнем фильтрации считается задержка 99,95% пыли или частиц не более 0,3 микрона. Для того, чтобы добиться этого показателя используется несколько ступеней очистки воздуха. Надо различать мощность работы электродвигателя, и мощность всасывания. Это не одно и то же, хотя и друг с другом они взаимосвязаны. Мощность, указываемая на упаковках, как правило, это пиковая мощность, которую может выдать двигатель. Но работать на ней он может ограниченное время. И эксплуатировать пылесос в таком режиме, это прямой путь к поломке агрегата. Мощность всасывания в 2-3 раза меньше мощности работы двигателя. Почему? Да, потому что мощность двигателя рассеивается на реализацию других функций пылесоса. Так, что если на коробке пылесоса указана мощность в 1500 Вт, то хорошо, если мощность всасывания составит 500 Вт. 2. Пылесосы с мешками Классический пылесос, не так уж сильно изменившийся с 1950-х годов, собирает пыль в мешок. Такие модели дешевы и очень широко распространены. Пыль при уборке попадает в специальный мешок-пылесборник, сделанный из ткани или бумаги. Воздух проходит через систему фильтров, улавливающих далеко не все частички пыли, и возвращается в комнату. Другой минус пылесосов с пылесборником — сам пылесборник, который быстро становится «родным домом» для клещей-сапрофитов и вредоносных микроорганизмов. Этого можно избежать, если менять мешок для пыли после каждой уборки, однако в таком случае пылесос станет очень дорогим в эксплуатации. В некоторых моделях допускается использование, как одноразовых бумажных мешков, так и многоразовых тканевых мешков. Бумажные мешки намного эффективней собирают мелкие частицы пыли, но по мере заполнения их приходится выкидывать (в среднем одного мешка объемом 3 литра хватает на месяц уборки). Возможность использования тканевых мешков обычно делается на тот случай когда, одноразовые закончились, а новые не успели купить. Частое же применение тканевых мешков не рекомендуется, поскольку они недостаточны эффективны. А это может стать причиной быстрого засорения дополнительных фильтров. При заполнении мешка постепенно снижается мощность всасывания. . Пылесосы с пыле

Круговое рассуждение Примеры ошибок

Круговое рассуждение (от латинского Circulus в Demonstrando ) происходит, когда конец аргумента возвращается к началу, не доказав себя. Эта форма рассуждения считается прагматическим дефектом или неформальной ошибкой, а не формальной логической ошибкой, потому что она следует правильному образцу аргументации: A доказывает B. Однако, в отличие от логического аргумента, B зависит от истинности A, в результате чего оператор, чтобы вернуться к циклу.

Примеры круговых аргументов

Круговые рассуждения также известны как круговые вопросы или круговые гипотезы. Это легко заметить, потому что обе стороны аргумента, по сути, придерживаются одной и той же точки зрения. Например:

• Ребекку все любят, потому что она так популярна.

• Вы должны соблюдать закон, потому что нарушение закона незаконно.

• Новая книга Гарольда написана хорошо, потому что Гарольд — замечательный писатель.

• Америка — лучшее место для жизни, потому что она лучше любой другой страны.

• Жестокие видеоигры побуждают подростков к насилию, потому что жестокие подростки играют в жестокие видеоигры.

Все эти утверждения заставляют слушателя спрашивать: «Но как вы можете быть так уверены?» Они не предлагают никаких веских доказательств, кроме утверждения, что A доказывает B.

Циклическое мышление в политике

Политики хорошо разбираются в риторике, но часто могут испортить свои аргументы циркулярной аргументацией.Обычный политический пример включает объяснение того, что определенная политика не должна быть законной, потому что она еще не законна. Другим примером может быть то, что избранное должностное лицо следует уважать, потому что оно является избранным должностным лицом.

Современное использование круговой аргументации основывается на вере слушателя в «фейковые новости», чтобы утверждать, что негативное освещение в прессе не соответствует действительности. Затем политик использует негативное освещение в прессе как доказательство того, что новости не соответствуют действительности.

Посмотрите на эту цитату Дональда Трампа в феврале 2017 года:

«Новости фальшивые, потому что большая часть новостей фальшивая.«

Круговые аргументы и парадоксы

Возможно, самый известный литературный пример кругового рассуждения, ведущего к парадоксу — или ситуации, в которой не могут существовать две реальности, — это общий вопрос« Что было первым: курица или яйцо? ».

Читатели оказываются на круговой дороге:

• Цыпленок должен происходить из яйца.

• Но яйцо не может существовать без курицы, несущей его.

• Но курица должна происходить из яйца. яйцо…

Уловка-22 Ситуации

Популярным литературным примером кругового рассуждения является заглавная «уловка» из «Уловки-22» Джозефа Хеллера.

«Конечно, есть загвоздка», — ответил Док Даника. «Уловка-22. Тот, кто хочет выйти из боевого дежурства, на самом деле не сумасшедший».

Рассказчик объясняет, что единственный способ избежать воздушного боя — заявить о невменяемости; однако осознание опасности этих миссий укрепляло здравомыслие. Фраза «уловка 22» превратилась в разговорный язык, в котором говорится, что вы оказались в ловушке кругового спора без выхода.

Напрашивающийся вопрос

В грубом переводе с латинского слова Petitio Principii, напрашивающийся вопрос описывает аргумент, который предполагает, что первая часть истинна, чтобы доказать вторую — во многом как круговое рассуждение.Фактически, современное использование часто считает эти концепции взаимозаменяемыми.

Однако в циркулярности аргумента, разделяющего их, есть некоторые нюансы.

Циклические примеры попрошайничества

Спрашивание вопроса Аргументы также могут быть круговыми аргументами. Например:

Восемнадцатилетние люди имеют право голосовать, потому что они разрешены к голосованию.

Этот аргумент является циркулярным, потому что он восходит к самому началу: 18-летние имеют право голоса, потому что это законно.Для них законно голосовать, потому что они имеют право голоса. Слушателю требуется дополнительное свидетельство, чтобы выйти из цикла аргументов.

Некруглые примеры напрашивания вопроса

Поскольку напрашивание вопроса просто требует, чтобы вы принимали первую часть аргумента, он не обязательно должен быть круговым. Например:

Восемнадцатилетние взрослые, поэтому они должны иметь право голоса.

Слушателя просят предположить, что 18-летние взрослые, чтобы согласиться с тем, что они должны иметь право голоса.Аргумент не является круговым, потому что им не нужно соглашаться со своим правом голоса, чтобы согласиться с тем, что они созрели.

Прекращение кругового аргумента

Лучший способ выйти из кругового аргумента — это запросить дополнительные доказательства. Спорите ли вы с кем-то, кто полагается на его выводы, чтобы доказать свою посылку, или вы пишете потенциально круговой аргумент в эссе, добавление внешних доказательств может положить конец петле. Чтобы аргумент не превратился в круговерть, важно быть открытым к изменению своего мнения на основе доказательств.

Больше логических заблуждений

Устранение заблуждений — важный шаг при создании риторических аргументов. Узнайте больше о других логических заблуждениях — таких как ошибка соломенного человека, основанная на атаке на искаженную версию исходного утверждения, или заблуждение post hoc ergo propter hoc, которое предполагает причинно-следственную связь там, где она может не существовать, — чтобы убедиться, что ваша аргумент действительно верен. Вот как можно избежать ошибочного утверждения!

Круговых примеров ошибочных рассуждений.

Пример программирования круговой интерполяции 1

Этот пример программирования круговой интерполяции покажет вам, что такое круговая интерполяция и как ее программировать.

Перед выполнением этого упражнения вы должны сначала прочитать статьи Circular Interpolation Concepts & Programming (перечисленные ниже). После прочтения статей вам будет удобно понять этот пример как очень простую и базовую работу.

Концепции и статьи по программированию с круговой интерполяцией

Пример программирования с круговой интерполяцией 1 (использование R)

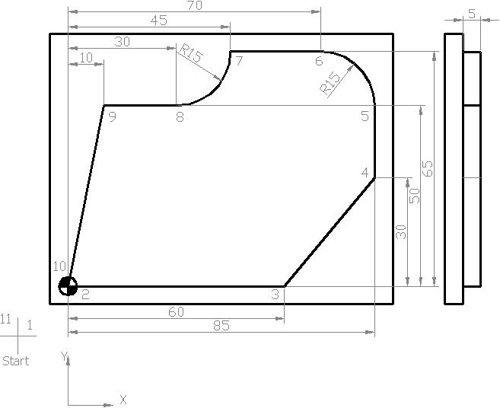
Пример программирования с круговой интерполяцией

 N5 G00 G54 G64 G90 G17 X-20 Y-20 Z50
N10 S450 M03 F250 D01 (12.5 ММ ДИАМ.)
N15 C0
N20 Z5
N25 G01 Z0
N30 Z-5
N35 G42 X0 Y0 M08 (движение лайнера)
N40 X60 Y0 (движение лайнера)
N45 X85 Y30 (движение лайнера)
N50 X85 Y50 (движение лайнера)
N55 G03 X70 Y65 U15 (Круговое движение G03 для движения против часовой стрелки и U для радиуса дуги)
N60 G01 X45 Y65 (движение лайнера)
N65 G02 X30 Y50 U15 (Круговое движение G02 для движения по часовой стрелке и U для радиуса дуги)
N70 G01 X10 Y50 (движение лайнера)
N75 X0 Y0 (движение лайнера)
N80 G40 X-20 Y-20
N85 G00 Z50 M09
N90 Y100
N95 M30 

Готовая деталь
После завершения процесса обработки ваша работа будет выглядеть следующим образом.

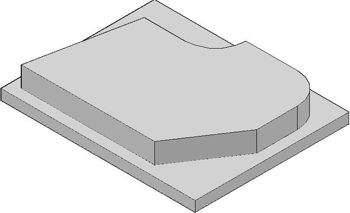
Обработанный компонент

Объяснение программы ЧПУ

В этом кадре программы ЧПУ № N35 — N50 (точки 2-3, 3-4, 4-5) находятся в прямом движении (линейная интерполяция), и для этого у нас есть G-код ЧПУ G01 (линейная интерполяция),

Точка 5-6 не является возможно с кодом G01, потому что инструмент не идет прямо, инструмент движется по кругу, для этой цели у станков с ЧПУ есть коды круговой интерполяции G02 / G03.
Перед использованием кода G02 / G03 станки с ЧПУ должны знать точные значения
(1) Конечная точка
(2) Радиус между начальной и конечной точками.
Итак, требуемые значения в точке 6:
(1) X = 70, Y = 65 (как конечная точка)
(2) R = 15 (как радиус).
После получения этой информации мы теперь в состоянии написать код блока программы ЧПУ для точек с 5 по 6.
Первое круговое движение G02-G03, второе — конечная точка X, значения Y и третье — R (радиус), таким образом мы можем достичь требуемых результатов.

Точка 6-7 снова является линейной, а точка 7-8 — круговым движением, поэтому сделайте то же самое, что указано выше, но перед написанием кода проверьте направление движения, по часовой стрелке или против часовой стрелки, и это движение по часовой стрелке, поэтому используйте код G02.

После этого остальные точки являются линейными перемещениями.

Каждое линейное движение отменяется круговым перемещением (G01 отменяется G02 / G03), и каждое круговое движение отменяется линейным перемещением (G02 / G03 отменяется G01)

Системная программа инкрементального измерения

Здесь это та же программа с ЧПУ, но с системой инкрементальных размеров G91.

 N35 G42 X0 Y0 M08 (движение лайнера)
N40 G91 X60 Y0 (движение лайнера)
N45 X25 Y30 (движение лайнера)
N50 X0 Y20 (движение лайнера)
N55 G03 X-15 Y15 U15 (Круговое движение G03 для движения против часовой стрелки и U для радиуса дуги)
N60 G01 X-25 Y0 (движение лайнера)
N65 G02 X-15 Y-15 U15 (Круговое движение G02 для движения по часовой стрелке и U для радиуса дуги)
N70 G01 X-20 Y0 (движение лайнера)
N75 X-10 Y-50 (движение лайнера) 

Объяснение G-кода / M-кода ЧПУ / S, F, D

G00: Ускоренный ход.
G54: нулевое смещение № 1.
G64: режим непрерывного пути.
G90: Абсолютная система размеров.
G17: выбор плана X-Y.
G42: активация компенсации радиуса фрезы (движение вправо)
G40: компенсация радиуса фрезы деактивирована
G02: круговая интерполяция по часовой стрелке
G03: круговая интерполяция против часовой стрелки (против часовой стрелки)
S: скорость шпинделя
F: движение оси подача
M: Движение резца (3 = по часовой стрелке, 4 = против часовой стрелки)
D: Инструмент №
M08: Охлаждающая жидкость включена
M09: Охлаждающая жидкость выключена
M30: Конец основной программы

.

Концепции круговой интерполяции и программирование, часть 3 (Использование I J K)

3-я часть многосерийных статей «Концепции и программирование круговой интерполяции».
В этой части кратко объясняется, как станки с ЧПУ могут рассчитать и запрограммировать круговую интерполяцию G02 G03 с использованием I J и K .

Прочтите другие части этой статьи

Круговая интерполяция G02 G03 I, J, K Концепции и программирование

Ось дуги должна быть параллельна оси X, Y или Z системы координат станка .Ось или плоскость, перпендикулярная оси, выбирается с помощью G17 (ось Z, плоскость XY), G18 (ось Y, плоскость XZ) или G19 (ось X, плоскость YZ). I, J и K — смещения от текущего местоположения. Одновременно будут использоваться только два из I, J и K. Это будет зависеть от того, какая плоскость дуги была выбрана.

• G17 — Используйте I и J
• G18 — Используйте I и K
• G19 — Используйте J и K

Аргументы I, J и K определяют РАССТОЯНИЕ от ТОЧКА НАЧАЛА дуги к ЦЕНТРАЛЬНОЙ ТОЧКЕ дуги.Обратите внимание, что начальная точка дуги НЕ УКАЗАНА в команде G02 или G03. Начальная точка определяется положением фрезы при выполнении команды. Кроме того, центральная точка никогда не указывается явно в команде. I, J и K — РАССТОЯНИЯ. Если геометрия круга невозможна (с точностью до 0,0001), обычно выдается ошибка.

На следующем рисунке показаны четыре квадранта круга и расчет I, J от начальной до конечной точки. Радиус круга 50 мм.

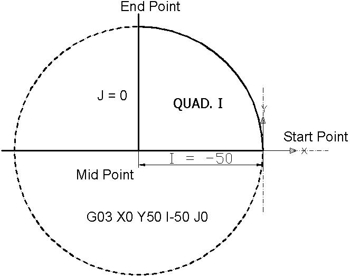Quad I от 0⁰ до 90⁰ — концепции круговой интерполяции Quad I от 0 ⁰ до 90 ⁰ Начальная точка X50 Y0 Конечная точка X0 Y50 I -50 J 0 G03 X0 Y50 I-50 J0

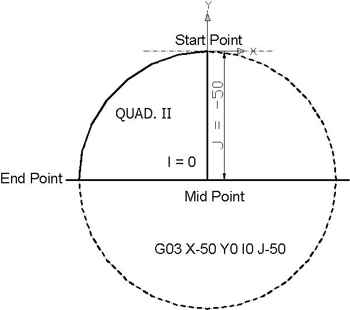Quad II от От 90⁰ до 180⁰ — концепции круговой интерполяции Quad II от 90 ⁰ до 180 ⁰ Начальная точка X0 Y50 Конечная точка X-50 Y0 I 0 J -50 G03 X-50 Y0 I0 J-50

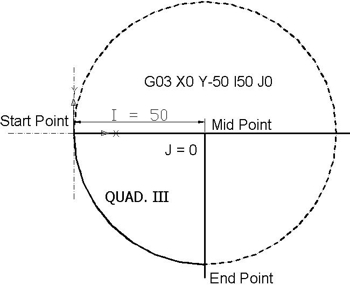Quad III от 180 ° до 270 ° — концепции круговой интерполяции Quad III от 180 ⁰ до 270 ⁰ Начальная точка X-50 Y0 Конечная точка X0 Y-50 I 50 J 0 G03 X0 Y-50 I50 J0

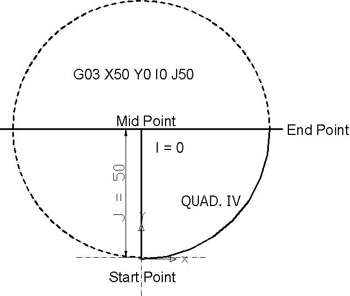Quad IV от 270⁰ до 0⁰ — концепции круговой интерполяции 9 0079 Quad IV от 270 ⁰ до 0 ⁰ Начальная точка X0 Y-50 Конечная точка X50 Y0 I 0 J 50 G03 X50 Y0 I0 J50

Прочтите другие части этой статьи

.

Концепции круговой интерполяции и программирование, часть 1 (Концепции)

Это серия статей для машинистов / программистов с ЧПУ, объясняющих концепции и методы программирования круговой интерполяции.
Без сомнения, каждый компонент в цехе обработки с ЧПУ имеет что-то вроде дуги, радиуса, окружности, поэтому не только необходимо, но и необходимо научиться программировать эти дуги, радиус, окружности, а также изучить основные концепции, основы круга и круговая интерполяция.

Прочтите другие части этой статьи

Итак, вкратце, мы только что изложили серию статей / руководств, чтобы облегчить эту работу для машинистов с ЧПУ / программистов ЧПУ и для новичков в ЧПУ, которые только начали посещать классы ЧПУ.

ЧТО ТАКОЕ ЦИРКУЛЯРНАЯ ИНТЕРПОЛЯЦИЯ

Концепции круговой интерполяции Программирование, часть 1

Определение

Преобразование положений линейной оси в изогнутые движения инструмента называется круговой интерполяцией. Другое определение — «Команды круговой интерполяции используются для перемещения инструмента по дуге окружности в заданное конечное положение».

Круговая интерполяция требует пяти единиц информации; конечная точка, скорость подачи, центр, радиус и направление движения.Круговая интерполяция — это движение инструмента по окружности. Это может быть полный круг или меньше.

Прежде чем перейти к обсуждению пяти частей информации для круговой интерполяции, сначала очень важно понять элементы круга в деталях.

ЭЛЕМЕНТЫ КРУГА

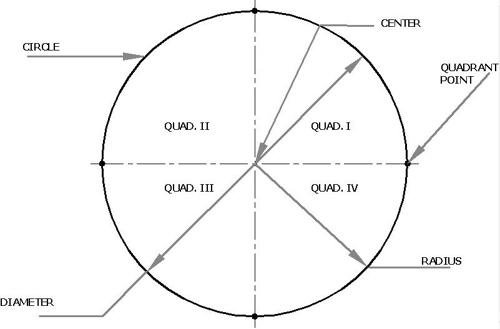
ЭЛЕМЕНТЫ КРУГА

ОПРЕДЕЛЕНИЕ КРУГА

Окружность определяется как замкнутая кривая на плоскости, где все точки находятся на одинаковом расстоянии от внутренней точки, называемой центральной точкой круга. .

РАДИУС

Радиус круга — это отрезок прямой от центральной точки до любой точки на окружности.

ДИАМЕТР

Диаметр круга — это отрезок прямой, проходящий через центральную точку круга и имеющий обе конечные точки на окружности.

КВАДРАНТ

Квадрант — это любая из четырех частей плоскости, образованных системой прямоугольных координат.

Каждому программисту полезно понимать концепцию квадрантов и их применение для круговых движений в программах фрезерования и токарной обработки.Окружность программируется во всех четырех квадрантах из-за своей природы, в то время как большинство дуг программируются в пределах одного или двух квадрантов. При программировании векторов дуги I, J и K угловая разница между начальной и конечной точками дуги не имеет значения. Единственная цель векторов дуги — определить уникальный радиус дуги между двумя точками.

Прочитать другие части этой статьи

.