Золотое сечение и симметрия — Мастерок.жж.рф — LiveJournal
? LiveJournal- Main
- Ratings
- Interesting
- iOS & Android
- Login
- CREATE BLOG Join
- English (en)
Золотая пропорция
Золотое сечение – это универсальное проявление структурной гармонии.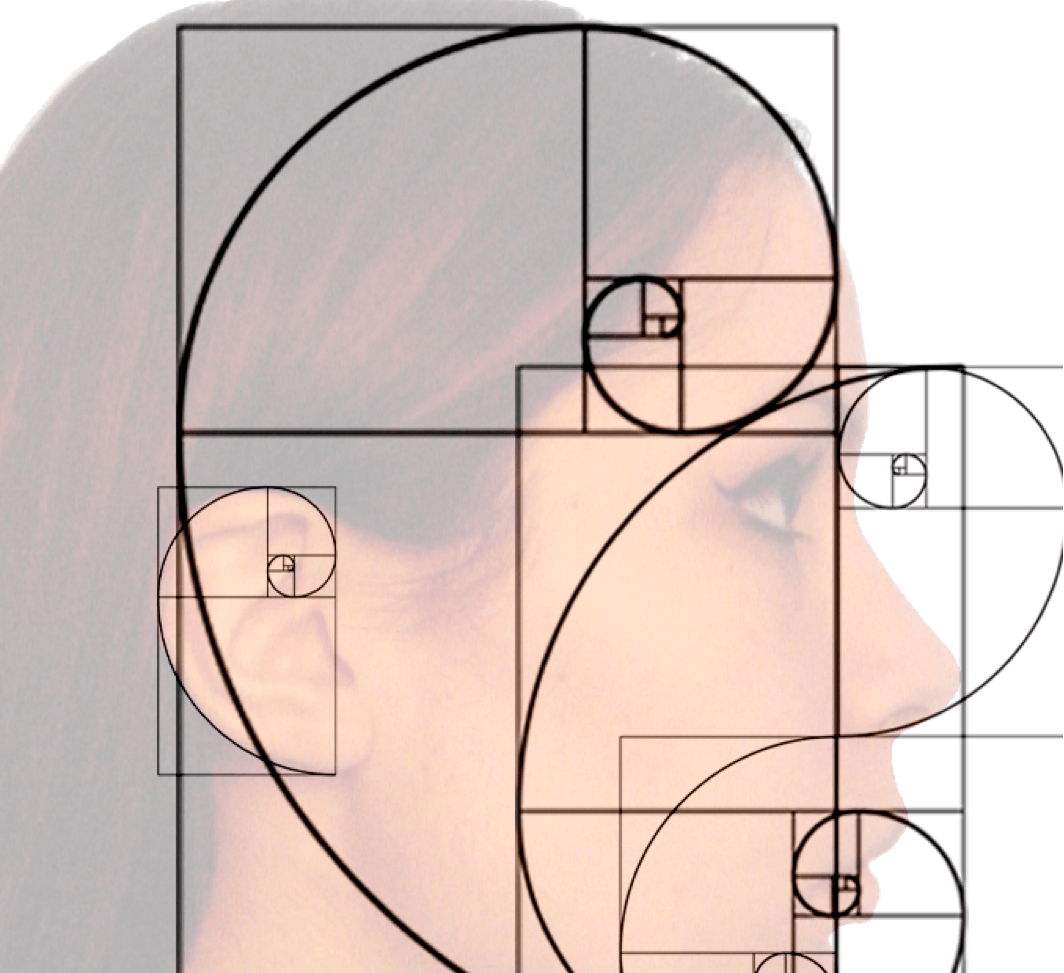
Наиболее ёмкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.
История
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция», иллюстрации к которой предположительно сделал Леонардо да Винчи.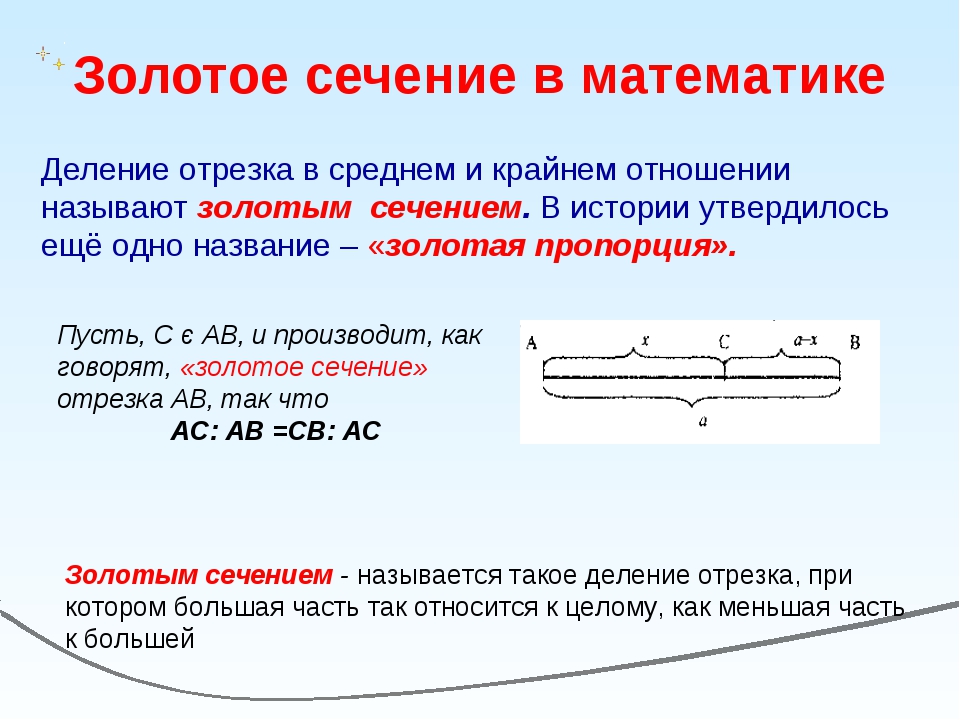
Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д.
На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до безконечности». Сейчас ряд Фибоначчи – это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин.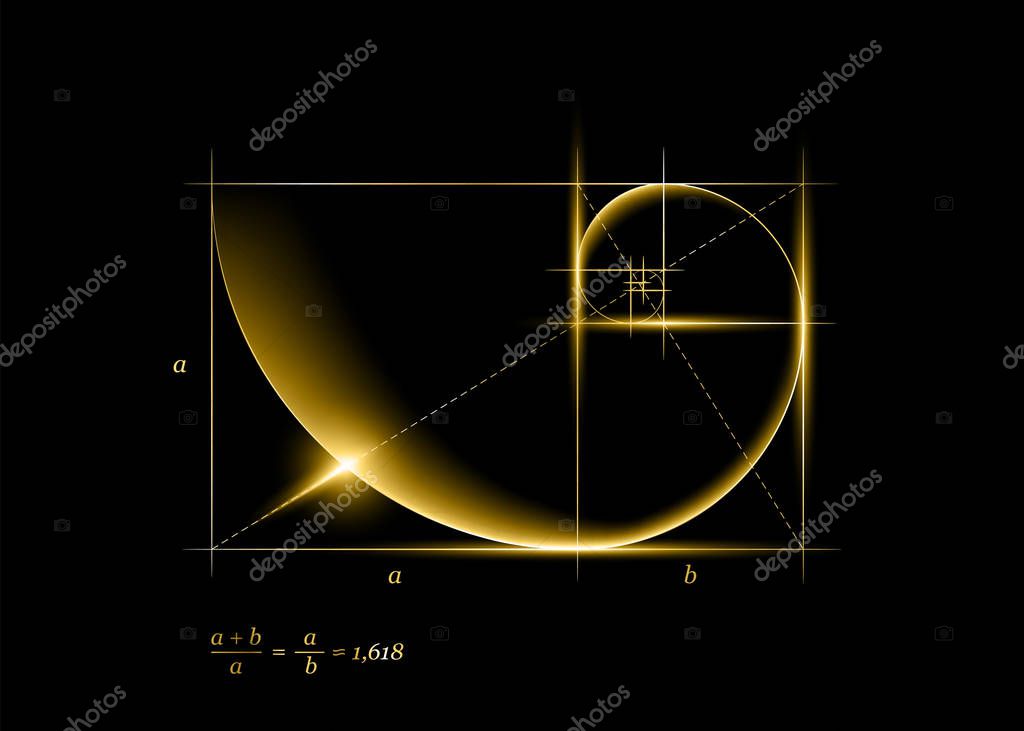 Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.
Природа
Самым удивительным в золотом сечении является то, что оно может рассматриваться как естественное явление в природе. Золотое сечение выражается в расположении ветвей вдоль стволов деревьев, прожилок в листьях. Его можно увидеть в строении скелетов животных и людей, в разветвлении их вен и нервов.
Оно даже может быть замечено в пропорции химических соединений и геометрии кристаллов.
Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять своё место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
По его мнению, одна из самых интересных форм это закручивание по спирали.
Ещё Архимед, уделяя внимание спирали, вывел на основе её формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни».
Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
Человек
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.
В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях.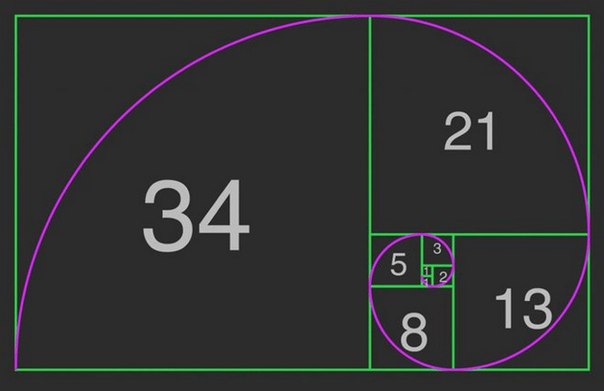 Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.
Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.
Искусство пространственных форм
Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.
Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции.
Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.
Слово, звук и кинолента
Формы временного искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.
Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.
Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера.
Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.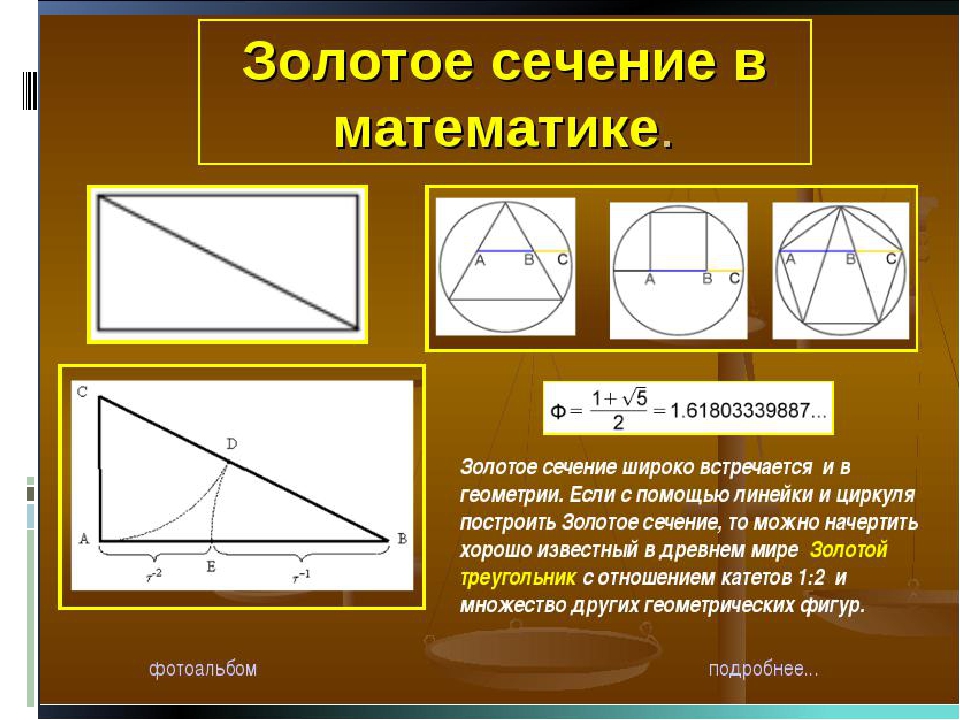
В фотографии и видеопроизводстве методика золотого сечения также используется повсеместно.
По сути, Золотая пропорция вокруг и внутри нас, и по этой причине немецкий психолог Адольф Цейзинг (1810 – 1876 гг.) назвал его «универсальным законом, в котором содержится основной принцип формирования всего, стремление к красоте и полноте в природе и искусстве, который пронизывает, как первостепенный духовный идеал, все структуры, формы и пропорции, будь то космические или индивидуальные, органические или неорганические, акустические или оптические; который полностью реализован в теле человека».
Благодаря уникальным свойствам золотого сечения многие считают его священным или божественным, позволяющим обрести более глубокое понимание красоты и духовности в жизни, увидеть скрытую гармонию и связность во всём, что нас окружает.
Источник: http://econet.ru/articles/149170-zolotoe-sechenie-kak-eto-rabotaet
Золотое сечение в архитектуре, строительстве, дизайне
Главная » Разное » Правило золотого сечения в архитектуре, строительстве и дизайне
Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…
Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…
Содержание статьи
Что такое золотое сечение и как его понимать
Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.
Сохранившиеся постройки древности тоже подчинены правилу золотого сечения
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Принцип и формула золотого сечения
На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Последовательность Фибоначчи — не только математическая формула
Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Построение прямоугольника с золотым сечением
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы.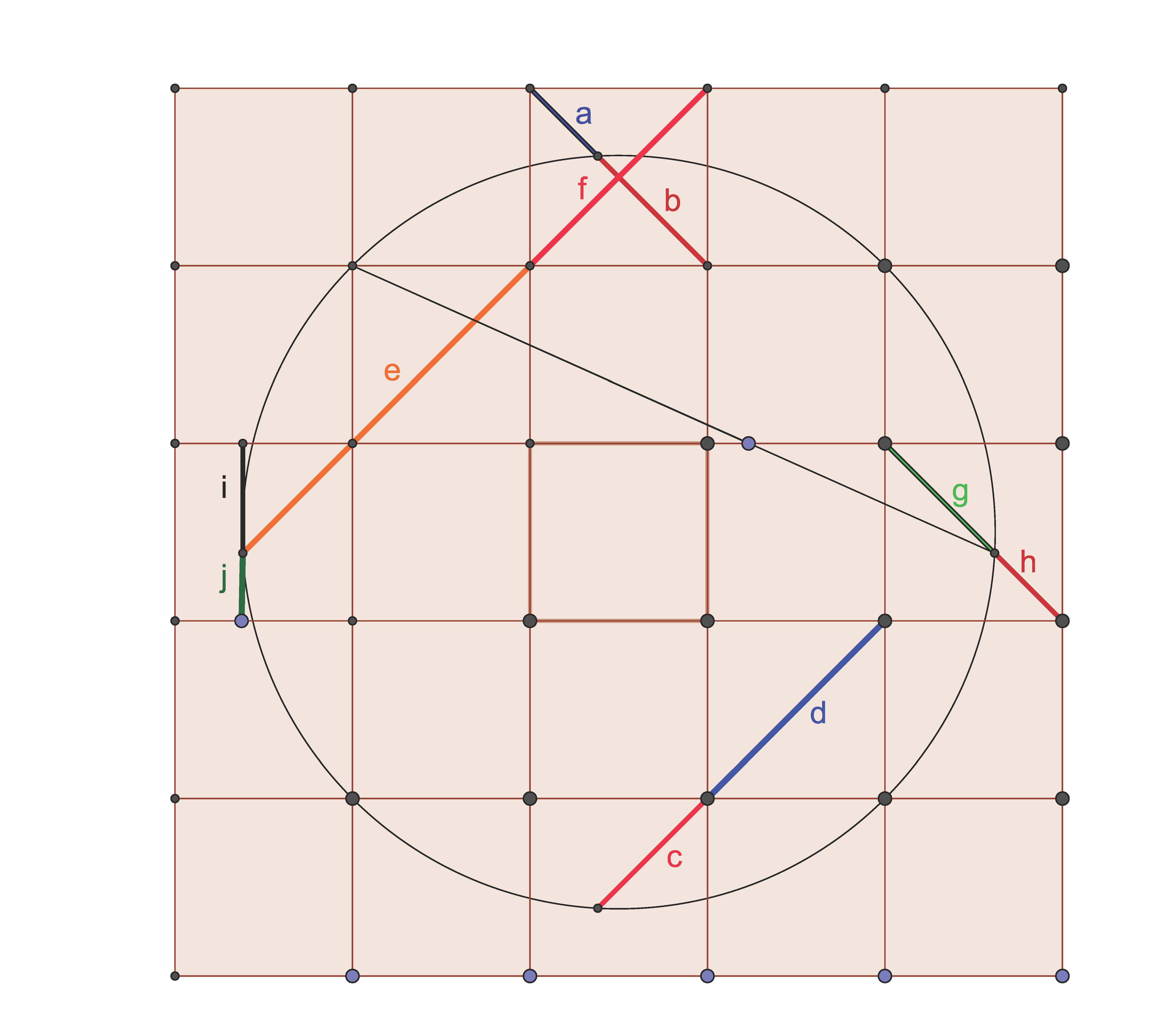 Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т. д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.
д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.
Ничего особенного, но взгляд не оторвать. Знаете почему?
Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.
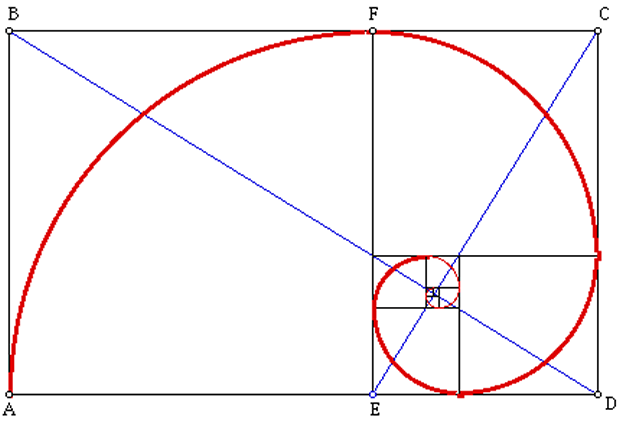
Деление отрезка на участки с идеальным соотношением
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр.
 Это точка D.
Это точка D.
Построение пентаграммы
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.
Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
Пример подбора цвета по правилам правильной пропорциональности
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты.
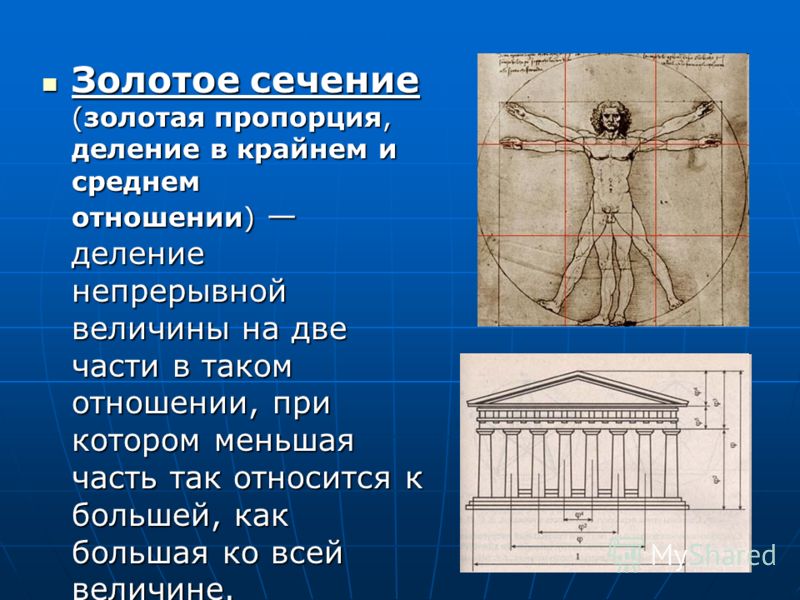 Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.
Пропорциональность — важная вещь
Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.
Правило треугольника в садовом дизайне
От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Правило золотого сечения в дизайне интерьера
Дата публикации: 06.07.2019
Формула идеальных гармоничных пропорций или правило «золотого сечения» известно человечеству с незапамятных времен. Его описывает Евклид в своих «Началах», о нем упоминает Пифагор. Руководствуясь этой формулой, великие архитекторы проектировали Парфенон, египетские пирамиды, Тадж-Махал, Храм Василия Блаженного. Тот же принцип использовали Фидий, Леонардо Да Винчи, Микеланджело, знаменитые художники, математики, композиторы. Определение золотого сечения в дизайне помогает создавать удивительно гармоничные пространства, в которых приятно находиться и комфортно жить.
Определение золотого сечения в дизайне помогает создавать удивительно гармоничные пространства, в которых приятно находиться и комфортно жить.
Общие принципы и определение
Суть правила «золотого сечения» сводится к тому, что большая часть целого относится к целому точно так же, как и меньшая часть – к большей части и наоборот. В цифровом выражении эта пропорция равна примерно 1,618, иначе это число называют числом «Фи», в честь древнегреческого архитектора Фидия. Если рассматривать правило в процентном соотношении, то большая часть составляет 62% от целой величины, а меньшая – около 38%.
То же определение легко сформулировать иначе. Так, в геометрии принято изображать «золотой прямоугольник», меньшая из сторон которого относится к большей как 0,618 к 1. Если от этого прямоугольника «отрезать» квадрат со стороной, равной меньшей из сторон, вы получите новый «золотой прямоугольник», и так – до бесконечности. В итоге искомые прямоугольники образуют своего рода спираль.
Золотое сечение в природе
Самое удивительное состоит в том, что человек лишь дал определение золотому сечению, записав его формулу. В природе этому правилу подчиняется строение многих предметов и объектов, к появлению которых люди не имеют никакого отношения. В качестве примеров можно привести ракушки улиток, моллюсков, рога животных, расположение лепестков цветов, семечек подсолнуха, «чешуек» ананасов и шишек, фаланги человеческих пальцев и многое другое.
Золотое сечение в: дизайне искусстве природе жизни
Золотое сечение — божественная пропорция: самое загадочное правило дизайна вызывает много споров. Разбираемся, как использовать его, чтобы ваши дизайны выделялись.
Что общего у пирамиды в Гизе и Мона Лизы с логотипом Пепси? И то, и другое создано с помощью золотого сечения. В этой статье мы разберем, что это такое и как его использовать в создании дизайна.
Правило золотого сечения
Золотое сечение — пропорция, которую заметили еще древние египтяне. Чтобы её получить, нужно разделить линию на две части так, чтобы длинная часть соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной. Оказывается, эта пропорция всегда равняется 1,618. Это число еще называют числом «фи».
Чтобы её получить, нужно разделить линию на две части так, чтобы длинная часть соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной. Оказывается, эта пропорция всегда равняется 1,618. Это число еще называют числом «фи».
Сохранившиеся постройки древности тоже подчинены правилу золотого сечения
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Принцип и формула золотого сечения
На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a.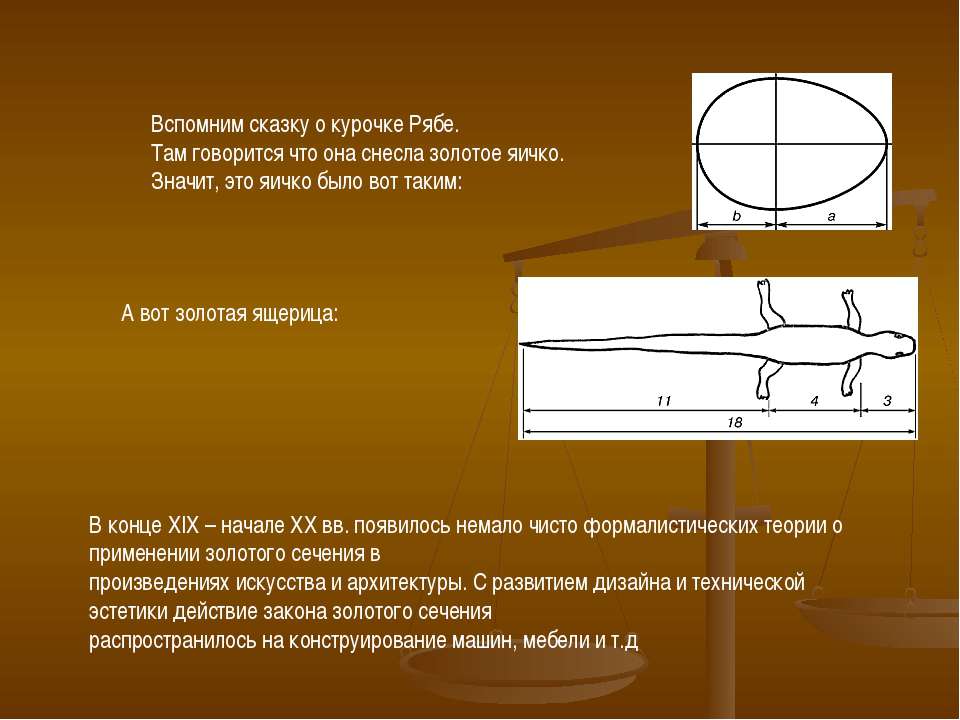 Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Последовательность Фибоначчи — не только математическая формула
Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Построение прямоугольника с золотым сечением
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.
Ничего особенного, но взгляд не оторвать. Знаете почему?
Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D.
 Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой. - Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.
Деление отрезка на участки с идеальным соотношением
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.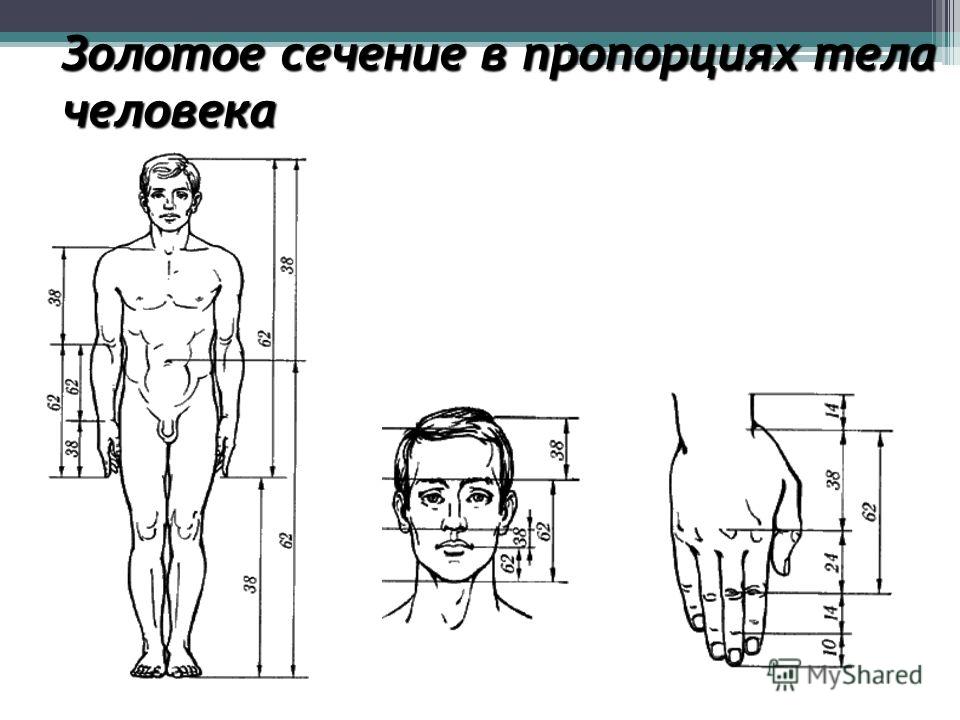
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C).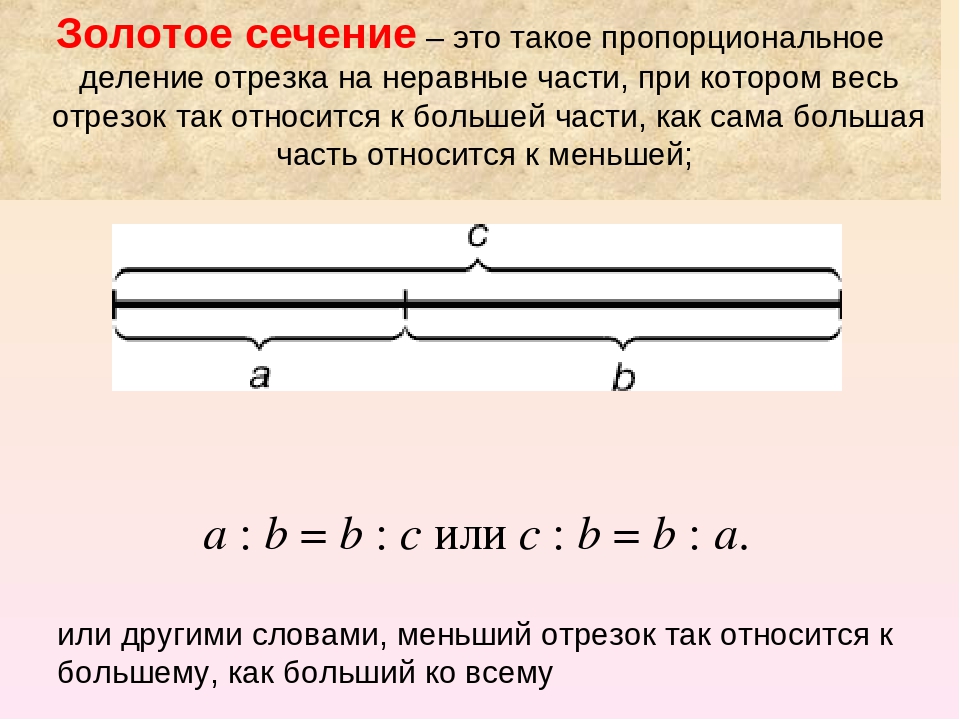 Вторая проверка — противолежащий угол составляет 36°.
Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
Построение пентаграммы
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.
Не только прямые линии можно использовать
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
Пример подбора цвета по правилам правильной пропорциональности - При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.
Пропорциональность — важная вещьПочему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Золотое сечение в ландшафтном дизайне
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.
Правило треугольника в садовом дизайнеОт главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Золотое сечение | Блог 4brain
Золотым сечением называют число, полученное путем деления линии на две части таким образом, что более длинная часть (а), разделенная на меньшую часть (b), равна полной длине линии (а+b), разделенной на более длинную часть (а). Такое отношение часто символизируют с помощью литеры Ф (читается как «фи») – 21-й буквы греческого алфавита. В форме уравнения это выглядит так:
a / b = (a + b) / a = 1.6180339887498948420…
Как и в случае с π (пи, отношение длины окружности к ее диаметру), число Ф является бесконечным. Обычно его округляют до значения 1,618.
История открытия золотой середины
Это число было найдено и открыто много раз, поэтому у него так много разных названий — золотая середина, золотое сечение, божественная пропорция и т.д. Исторически его можно увидеть в архитектуре многих древних творений, таких как Великие Пирамиды и Парфенон. В пирамиде Гизы длина каждой стороны основания составляет 230,5 метров при высоте 146,6 метров. Отношение основания к высоте составляет примерно 1,5717, что близко к золотой пропорции.
Фидий (500 г. до н.э. — 432 г. до н.э.) был греческим скульптором и математиком, который, как считается, применил Ф, создавая скульптуры для Парфенона. Платон (428 г. до н.э. — 347 г. до н.э.) считал, что золотое сечение является наиболее универсальным связующим звеном математических отношений. Позднее Евклид (365 г. до н.э. — 300 г. до н.э.) связал золотое сечение с построением пентаграммы.
Последовательность Фибоначчи и золотое сечение
Около 1200 года математик Леонардо Фибоначчи открыл уникальные свойства последовательности Фибоначчи. Эта последовательность непосредственно связана с золотым сечением, потому что если взять любые два последовательных числа Фибоначчи, их отношение будет очень близко к золотому сечению. По мере того как числа возрастают, соотношение приближается к значению 1,618. Например, соотношение 3 к 5 составляет 1,666. Но соотношение 13 к 21 составляет 1,625. Возрастая, соотношение 144 к 233 составляет 1,618. Все эти числа являются последовательными числами в последовательности Фибоначчи.
Такие соотношения из ряда Фибоначчи, близкие к значению золотого сечения, могут быть применены к пропорциям прямоугольника, называемого золотым прямоугольником. Он известен как одна из наиболее визуально совершенных из всех геометрических форм — следовательно, правило золотого сечения очень широко применяется во всех видах визуального искусства. Золотой прямоугольник также связан с золотой спиралью, которая создается путем создания смежных квадратов измерений Фибоначчи.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.
Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.
Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию. В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.
Фи — более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.
Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.
- Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
- Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
- Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
- Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
- Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
- Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
- Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
- Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
- Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
- Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.
Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.
идеальный раздел — это … Что такое идеальный раздел?
Ideal-type — Idéal type Единственный тип — это определенная социологическая концепция Макса Вебера. Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des…… Wikipédia en Français
Idéal-Type — Un idéal type — это определенная социологическая концепция Макса Вебера. Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques.L idéal type sera par la suite réutilisé par des théoriciens des…… Wikipédia en Français
Idéal-typique — Idéal type Un idéal type — это определенная социологическая концепция Макса Вебера. Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des…… Wikipédia en Français
Идентификационный тип — Уникальный тип — это определенная социологическая концепция Макса Вебера.Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des théoriciens des…… Wikipédia en Français
Ideal Home — это название британского журнала по домашнему декору, который ежемесячно издается IPC Media, дочерней компанией Time Warner. Ideal Home — это самый продаваемый журнал о домах в Соединенном Королевстве (проверенный ABC тираж 233 630 экземпляров, январь июнь 2007 г.) и имеет…… Wikipedia
Идеальная школа и колледж — Infobox Название школы = Ideal School and College imagesize = 80px caption = Идеальная школа и колледж. Девиз с монограммой = установлен = 1965 type = Частная принадлежность = округ = классы = от 1 до 12 президент = директор = Ms.Рашида Бегум (Текущий…… Википедия
Idéal — Pour les article homonymes, voir Idéal (омонимы). En mathématiques, et plus specific en algèbre, un idéal est un sous ensemble remarquable d un anneau. Определенно, очевидно, что все идеи имеют видимость векторных пространств, которые являются…… Wikipédia en Français
Идеальная цепь — Идеальная цепь (или цепь со свободными соединениями) — это простейшая модель для описания полимера.Он принимает полимер только как случайное блуждание и игнорирует любые взаимодействия между мономерами. Хотя это просто, его обобщение дает нам некоторое представление…… Wikipedia
Section dorée — Nombre d or Pour l’article homonyme, voir Nombre d or (astronomie). Определенная пропорция, равная и лучшей, чем крайняя и моя, основанная на лорске… Wikipédia en Français
Идеал (теория колец) — В теории колец, ветви абстрактной алгебры, идеал — это особое подмножество кольца.Идеальная концепция позволяет надлежащим образом обобщать некоторые важные свойства целых чисел, такие как четное число или кратное 3. Например, в…… Википедии
Идеальный газ — Термодинамика… Википедия
Добро пожаловать в Project IDEAL Online
Об этом веб-сайте
С чего начать
Мы рекомендуем вам начать с просмотра видео справа, чтобы узнать о преподавании специального образования.Затем вы можете изучить модуль Категории инвалидности и ознакомиться с каждой категорией инвалидности. Не стесняйтесь изучать другие модули, дополнительную информацию и ресурсы по своему усмотрению. Кроме того, сайт IDEAL In Action — отличное место, чтобы узнать, как учителя используют идеи из Project Ideal в реальных учебных ситуациях.
Модули
Каждый учебный модуль имеет аналогичную структуру и включает в себя ключевые концепции, упражнения, презентации, тесты и средства массовой информации.Изучите ключевые концепции или перейдите в раздел «Действия», чтобы получить идеи о том, как реализовать то, что вы изучаете, в своих классах.
Особая благодарность
Финансовая поддержка проекта IDEAL предоставляется Техасским советом по нарушениям развития, а федеральные средства предоставлены Управлением по вопросам нарушений развития Министерства здравоохранения и социальных служб США.
Особая благодарность всем членам команды разработчиков Project IDEAL.
Project IDEAL в действии
Помимо веб-сайта Project IDEAL, мы разработали сайт IDEAL In Action. На этом сайте представлены видео-примеры того, как учителя используют идеи, разработанные и описанные в Project IDEAL, в своих классах.
Для навигации между двумя сайтами вы можете просто навести курсор на логотип в верхней части страницы.
Примечание о ссылках
Хотя Project IDEAL не может гарантировать точность этих отмеченных ресурсов, мы приложили все усилия, чтобы включить последнюю доступную информацию.Пожалуйста, свяжитесь с веб-мастером в правом верхнем углу этого веб-сайта, чтобы предоставить предложения и / или исправления для Project IDEAL относительно точности этих ресурсов. Project IDEAL не может контролировать доступность и точность внешних ссылок на веб-сайты; однако мы приложили все усилия, чтобы отметить те ресурсы, которые были бы полезны нашим читателям.
IDEAL WORKSTATION® 2C
НАТУРАЛЬНЫЙ ЗОЛОТОЙ БАМБУК
IWS-2-C-BA
ДЕРЕВЯННЫЙ КОМПОЗИТНЫЙ ГРАФИТ
IWS-2-C-GT
EXCLUSIVE GRAY RESIN
IWS-2-C-GR000
RESIN
DESIGNER IWS 2-C-WH
Выберите желаемую отделку Culinary Kit выше
Кулинарный набор из 4 инструментов, входящий в состав IWS-2-C
Доступны во всех четырех вариантах отделки *
(1) * Разделочная доска верхнего яруса 12 1/4 ″ x 18 ″
(1) * Стеллаж для сушки верхнего яруса 12 1/4 ″ x 18 ″
(1) * Платформа нижнего яруса для дуршлага, чаши для смешивания 12 1/4 ″ x 17 ″
(1) 7.Дуршлаг 2qt 11 ”с нескользящими ручками
(1) Чаша 7,2 литра, 11 дюймов с крышкой и нескользящим дном
Рабочее место на 1 человека
Нержавеющая сталь 316L
Сборная цельная деталь из морской нержавеющей стали 316L
с дизайном TrueEdge ™
Универсальный двухуровневый дизайн
Кулинарные инструменты скользят над и под каждым
другие на верхнем и нижнем ярусах
Ангел Финиш
Специальная ручная отделка для исключительного износа
и простоты обслуживания.
Раковина двусторонняя
Реверсивный бассейн с центральным сливом
Сделано в США
Каждая камбуз искусно изготовлена вручную, а
произведена в США
Повышенная сливная крышка
Приподнятая крышка слива закрывает слив
, позволяя воде течь свободно
br>
Наши универсальные кулинарные инструменты ограничены только вашим воображением.
Доска для приправ
Доступен в натуральном золотом бамбуке, композитном графитовом дереве, эксклюзивной серой смоле или дизайнерской белой смоле
Двухуровневый или верхний уровень
Доска для обслуживания приправ верхнего уровня
Этот многоцелевой сервер добавляет стиль, функциональность и гибкость вашему развлечению. Три контейнера (1 мелкий и 2 глубоких) расположены на платформе верхнего уровня, создавая заманчивую презентацию для любого вида буфета с едой. В комплекте три прозрачные крышки.
Натуральный золотистый бамбук, композит из графитового дерева, эксклюзивная серая смола или дизайнерская белая смола
Размеры 9 ″ x 18 ″
Доска для гарнира
Доступен в исполнении из натурального золотистого бамбука, композитного графита из дерева, эксклюзивной серой смолы или дизайнерской белой смолы
Верхний уровень
Корзина для посуды
Доступен в исполнении из натурального золотистого бамбука, композитного графита из дерева, эксклюзивной серой смолы или дизайнерской белой смолы
Верхний уровень
Разделочная доска для гарнира
Доступен в исполнении из натурального золотистого бамбука, композитного графитового дерева, эксклюзивной серой смолы или дизайнерской белой смолы
Верхний уровень
Набор для мытья и сервировки
Доступен в натуральном золотом бамбуке, композитном графитовом дереве, эксклюзивной серой смоле или дизайнерской белой смоле
Двухуровневый или верхний уровень
Набор для мытья посуды
Доступен в натуральном золотом бамбуке, композитном графитовом дереве, эксклюзивной серой смоле или дизайнерской белой смоле
Двухуровневый или верхний уровень
Сервировочный набор
Доступен в натуральном золотом бамбуке, композитном графитовом дереве, эксклюзивной серой смоле или дизайнерской белой смоле
Двухуровневый или верхний уровень
Блок ножей стойки
Доступен в корпусе из американского черного ореха, натурального золотистого бамбука или композитного дерева из графита
Верхний уровень
Примечание: ножи в комплект не входят
Характеристики установки
Сковорода для половинок
Доступен из алюминизированной стали
Верхний уровень
Доска для приправ
Этот многоцелевой сервер добавляет стиль, функциональность и гибкость вашему развлечению.Шесть контейнеров (3 неглубоких и 3 глубоких) размещены на двухъярусной платформе, создавая заманчивую презентацию для любого типа буфета с едой. В комплекте шесть прозрачных крышек.
Натуральный золотистый бамбук, композит из графитового дерева, эксклюзивная серая смола или дизайнерская белая смола
Размеры 17 ″ x 18 ″
Chef’s Block
Доступен в цвете американский черный орех и натуральный золотистый бамбук
Двухуровневый или верхний уровень
Набор для мытья и сервировки
Нужен отдельный бассейн? Бросьте это в камбуз, чтобы мыть бокалы вручную, или залейте льдом, чтобы подавать охлажденные напитки.Стопор и платформа включены.
Натуральный золотистый бамбук, композит из графитового дерева, эксклюзивная серая смола или дизайнерская белая смола
Размеры 17 ″ x 18 ″
Решетка нижняя
| Владельцы камбуза попросили, чтобы мы доставили! Это не просто нижние решетки, они изготовлены из прочной, жаропрочной нержавеющей стали, что делает их намного более прочными, чем любые решетки, которые мы видели. Доступны шесть полных наборов решеток для покрытия всей нижней части IWS любой длины.Хотите покрыть только часть рабочей станции? Выберите из индивидуальных решеток ниже. КОМПЛЕКТНЫЕ НАБОРЫ РЕШЕТОК ДЛЯ ОДИНОЧНОЙ ЧАШИ IWSIWS 7-S: BG-7-S-3-SS IWS 6-S: BG-6-S-3-SS IWS 5-S: BG-5-S-2-SS IWS 4-S: BG-4-S-2-SS IWS 3-S: BG-3-S-1-SS IWS 2-C: BG-2-C-1-SS КОМПЛЕКТНЫЕ НАБОРЫ РЕШЕТКИ ДЛЯ ДВОЙНЫХ ЧАШЕК IWS ИНДИВИДУАЛЬНЫЕ РЕШЕТКИ Примечание: S = боковое сливное отверстие; N = нет сливного отверстия; C = центральное сливное отверстие; D = Двойные сливные отверстия. |
Встраиваемый блок для ножей на столешнице
Низкопрофильный бамбуковый блок хранит столовые приборы там, где они нужны: на камбузе.Семь прорезей вмещают три больших ножа и четыре меньших ножа, а также ножницы и точилку в этом аксессуаре, который предназначен для встраивания в вашу столешницу.
Натуральный золотой бамбук и древесный графитовый композит
Размеры 3 1/2 ″ x 11 ″
Примечание. Ножи в комплект не входят.
Характеристики установки
Корзина фильтра
Вы можете увидеть по крайней мере одну камбуз на выставке в любом из выставочных залов нашего официального дилера. Найдите ближайший к вам с помощью кнопки «Найти выставочный зал» ниже.Если вы еще не встретили дилера или дистрибьютора в вашем районе, не волнуйтесь. Вы можете позвонить нам напрямую, чтобы разместить заказ.
Техническая информация Загрузки
IWS 2C Specification Sheet
IWS 2C Counter Top Cutout
IWS 2C CAD Plan View (DWG and DXF)
IWS 2C CAD 3D Model (DWG and DXF)
IWS 2C SketchUp 3D Model (SKP)
Инструкции по установке IWS
Видео по установке рабочей станции
Скачать каталог дизайна 2020
Обратите внимание: каталог будет работать только в версии 2020 Design 9 или новее.
Загрузить 3D-библиотеку главного архитектора
Общая информация
🎓 идеальный раздел ⚗ с английского на русский 🧬
— Idéal type Un idéal type is un concept sociologique defini от Макса Вебера. Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des…… Wikipédia en Français
Idéal-typique — Idéal type Un idéal type — это определенная социологическая концепция Макса Вебера.Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des…… Wikipédia en Français
Идентификационный тип — Уникальный тип — это определенная социологическая концепция Макса Вебера. Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des théoriciens des…… Wikipédia en Français
Ideal Home — это название британского журнала по домашнему декору, который ежемесячно издается IPC Media, дочерней компанией Time Warner.Ideal Home — это самый продаваемый журнал о домах в Соединенном Королевстве (проверенный ABC тираж 233 630 экземпляров, январь июнь 2007 г.) и имеет…… Wikipedia
Идеальная школа и колледж — Infobox Название школы = Ideal School and College imagesize = 80px caption = Идеальная школа и колледж. Девиз с монограммой = установлен = 1965 type = Частная принадлежность = округ = классы = от 1 до 12 президент = директор = Ms. Рашида Бегум (Текущий…… Википедия
Idéal — Pour les article homonymes, voir Idéal (омонимы).En mathématiques, et plus specific en algèbre, un idéal est un sous ensemble remarquable d un anneau. Определенно, очевидно, что все идеи имеют видимость векторных пространств, которые являются…… Wikipédia en Français
Идеальная цепь — Идеальная цепь (или цепь со свободными соединениями) — это простейшая модель для описания полимера. Он принимает полимер только как случайное блуждание и игнорирует любые взаимодействия между мономерами. Хотя это просто, его обобщение дает нам некоторое представление…… Wikipedia
Section dorée — Nombre d or Pour l’article homonyme, voir Nombre d or (astronomie).Определенная пропорция, равная и лучшей, чем крайняя и моя, основанная на лорске… Wikipédia en Français
Идеал (теория колец) — В теории колец, ветви абстрактной алгебры, идеал — это особое подмножество кольца. Идеальная концепция позволяет надлежащим образом обобщать некоторые важные свойства целых чисел, такие как четное число или кратное 3. Например, в…… Википедии
Идеальный газ — Термодинамика… Википедия
Idéal premier — Ричард Дедекинд 1831 1916 формализатор концепции идеи En algèbre commutative, un idéal premier d un anneau commutatif unitaire is un idéal tel que le quotient de l anneau par cet idéal est un anneau intègre.Ce concept généralise la notion… Wikipédia en Français
🎓 perfect section ⚗ von englisch auf russisch 🧬
— Idéal type Un idéal type is un concept sociologique defini par Max Weber. Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des…… Wikipédia en Français
Idéal-typique — Idéal type Un idéal type — это определенная социологическая концепция Макса Вебера.Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des…… Wikipédia en Français
Идентификационный тип — Уникальный тип — это определенная социологическая концепция Макса Вебера. Il vise, pour Weber, à bâtir un modèle d un phénomène social qu on cherche à étudier pour ses qualités intrinsèques. L idéal type sera par la suite réutilisé par des théoriciens des…… Wikipédia en Français
Ideal Home — это название британского журнала по домашнему декору, который ежемесячно издается IPC Media, дочерней компанией Time Warner.Ideal Home — это самый продаваемый журнал о домах в Соединенном Королевстве (проверенный ABC тираж 233 630 экземпляров, январь июнь 2007 г.) и имеет…… Wikipedia
Идеальная школа и колледж — Infobox Название школы = Ideal School and College imagesize = 80px caption = Идеальная школа и колледж. Девиз с монограммой = установлен = 1965 type = Частная принадлежность = округ = классы = от 1 до 12 президент = директор = Ms. Рашида Бегум (Текущий…… Википедия
Idéal — Pour les article homonymes, voir Idéal (омонимы).En mathématiques, et plus specific en algèbre, un idéal est un sous ensemble remarquable d un anneau. Определенно, очевидно, что все идеи имеют видимость векторных пространств, которые являются…… Wikipédia en Français
Идеальная цепь — Идеальная цепь (или цепь со свободными соединениями) — это простейшая модель для описания полимера. Он принимает полимер только как случайное блуждание и игнорирует любые взаимодействия между мономерами. Хотя это просто, его обобщение дает нам некоторое представление…… Wikipedia
Section dorée — Nombre d or Pour l’article homonyme, voir Nombre d or (astronomie).Определенная пропорция, равная и лучшей, чем крайняя и моя, основанная на лорске… Wikipédia en Français
Идеал (теория колец) — В теории колец, ветви абстрактной алгебры, идеал — это особое подмножество кольца. Идеальная концепция позволяет надлежащим образом обобщать некоторые важные свойства целых чисел, такие как четное число или кратное 3. Например, в…… Википедии
Идеальный газ — Термодинамика… Википедия
Idéal premier — Ричард Дедекинд 1831 1916 формализатор концепции идеи En algèbre commutative, un idéal premier d un anneau commutatif unitaire is un idéal tel que le quotient de l anneau par cet idéal est un anneau intègre.Ce concept généralise la notion… Wikipédia en Français

