Физические качества и их определения: Методика развития физических качеств Статьи

Содержание

Физические способности человека и их развитие

Введение

Еще в античный период древнегреческий мыслитель, философ Платон отмечал: “Воину необходимо иметь силу, быстроту, мужество. Эти качества необходимо иметь каждому воину”. В работе “Армия” Ф. Энгельс характеризует солдат будущего общества: “По силе, ловкости, интеллигентности они превзойдут тех солдат, которых может дать современное общество”. В наше время его взгляды являлись одной из предпосылок научных исследований и последующей специальной направленности физической подготовки войск с учетом конкретной воинской специальности.

Представление о физических качествах окончательно неупорядочено. Часть авторов рассматривает их как свойства и способности человека, другие – как стороны двигательной деятельности. Первое научное определение физическим качествам дал П.Ф. Лесгафт, рассматривая их как причину движения или его видоизменения. Сила – это способность производить механическую работу. Неутомимость – способность к длительному ее выполнению. Быстрота – способность управлять силой во времени. Ловкость – способность управлять ею в пространстве.

Для П.Ф. Лесгафта характерен физиолого-анатомический подход: сила – мышцы туловища, выносливость – мышцы ног, ловкость – мышцы рук. Он полагал, что физические качества зависят от химического состава мышц. Современные исследования выделяют в мышцах белые и красные волокна. Белые волокна способствуют проявлению скоростно-силовых параметров в активной двигательной деятельности, красные волокна – длительному выполнению работы. Так, у спринтеров мышцы ног содержат 75% белых волокон и 25% красных, а у стайеров наблюдается прямо противоположная картина.

Автор первого учебника по ТМФВ для вузов профессор А.Д. Новиков трактовал физические качества как выражение функциональной дееспособности организма к психофизическим напряжениям в процессе двигательной деятельности. Сила – способность к максимальным по величине напряжениям, быстрота – по интенсивности, выносливость – по длительности; ловкость – способность к максимальным по сложности психофизическим напряжениям.

В литературе встречается и такое определение: физические качества – это отдельные качественные стороны двигательной деятельности. Все вышеперечисленные определения верны, просто авторы акцентируют внимание в этих формулировках на своей позиции. Исследования в области биохимии спорта и теории функциональных систем приводят к заключению, что физические качества – это формы проявления физической активности, связанной с энергетическим обеспечением движений. Специфика проявления физических качеств определяется характером физической активности и со- ставом ведущих функциональных систем ее обеспечения.

На наш взгляд, отражает сущность и легко запоминается следующее определение: физические качества – это функциональные свойства организма, обеспечивающие активную двигательную деятельность. Физические качества, двигательные качества – равнозначные термины. Если хотят обратить внимание на психические и физиологические механизмы, то еще называют психомоторные качества.

Общие закономерности развития физических качеств:

1) развитие качеств происходит в процессе двигательной деятельности, требующей их проявления;

2) взаимосвязь качеств в процессе их развития;

3) постепенность и неравномерность развития качеств.

Развитие физических качеств происходит по фазам (этапам). На разных этапах это развитие происходит неодинаково. Так, на ранних этапах их воспитания (у начинающих спортсменов) развитие одного качества обусловливает и развитие других. На определенном этапе воспитания (как правило, у высококвалифицированных спортсменов) развитие одного качества может тормозить развитие других.

В возрастном аспекте развитие физических качеств отличается разновременностью (гетерохронностью). Скоростные качества достигают пика биологического развития в 13-15 лет, а силовые – в 25-30 лет. Разнонаправленность в развитии отдельных качеств особенно значительна в период полового созревания.

В школьном возрасте принято выделять периоды наиболее значительных возрастных изменений в организме, в том числе и в развитии физических качеств. Эти периоды получили название сенситивных (наиболее чувствительных). Целенаправленное воспитание конкретных качеств в сенситивных периодах дает наибольший эффект, т. к. обеспечивает наиболее высокие темпы их прироста.

Любое физическое качество – это биологическое свойство и способность использовать их в процессе активной деятельности. Следует также помнить, что уровень развития и проявления качеств в процессе активной двигательной деятельности определяется не только функциональными свойствами организма, но и его духовными качествами (волевыми усилиями).

1. Понятие о силе и силовых качествах

Люди всегда стремились быть сильными и всегда уважали силу.

Различают максимальную (абсолютную) силу, скоростную силу и силовую выносливость. Максимальная сила зависит от величины поперечного сечения мышцы. Скоростная сила определяется скоростью, с которой может быть выполнено силовое упражнение или силовой прием. А силовая выносливость определяется по числу повторений силового упражнения до крайней усталости.

Для развития максимальной силы выработан метод максимальных усилий, рассчитанный на развитие мышечной силы за счет повторения с максимальным усилием необходимого упражнения. для развития скоростной силы необходимо стремиться наращивать скорость выполнения упражнений или при той же скорости прибавлять нагрузку. Одновременно растет и максимальная сила, а на ней, как на платформе, формируется скоростная. Для развития силовой выносливости применяется метод «до отказа», заключающийся в непрерывном упражнении со средним усилием до полной усталости мышц.

Чтобы развить силу, нужно:

1. Укрепить мышечные группы всего двигательного аппарата.

2. Развить способности выдерживать различные усилия (динамические, статические и др.)

3. Приобрести умение рационально использовать свою силу.

Для быстрого роста силы необходимо постепенно, но неуклонно увеличивать вес отягощений и быстроту движений с этим весом. Сила особенно эффективно растет не от работы большой суммарной величины, а от кратковременных, но многократно интенсивно выполняемых упражнений. Решающее значение для формирования силы имеют последние попытки, выполняемые на фоне утомления. Для повышения эффективности занятий рекомендуется включать в них вслед за силовыми упражнениями упражнения динамические, способствующие расслаблению мышц и пробуждающие положительные эмоции – игры, плавание и т.п.

Уровень силы характеризует определенное морфофункциональное состояние мышечной системы, обеспечивающей двигательную, корсетную, насосную и обменную функции.

Корсетная функция обеспечивает при определенном мышечном тонусе нормальную осанку, а также функции позвоночника и спинного мозга, предупреждая такие распространенные нарушения и заболевания как дефекты осанки, сколиозы, остеохондрозы. Корсетная функция живота играет важную роль в функционировании печени, желудка, кишечника, почек, предупреждая такие заболевания как гастрит, колит, холецистит и др. недостаточный тонус мышц ног ведет к развитию плоскостопия, расширению вен и тромбофлебиту.

Недостаточное количество мышечных волокон, а значит, снижение обменных процессов в мышцах ведет к ожирению, атеросклерозу и другим неинфекционным заболеваниям.

Насосная функция мышц («мышечный насос») состоит в том, что сокращение либо статическое напряжение мышц способствует передвижению венозной крови по направлению к сердцу, что имеет большое значение при обеспечении общего кровотока и лимфотока. «Мышечный насос» развивает силу, превышающую работу сердечной мышцы и обеспечивает наполнение правого желудочка необходимым количеством крови. Кроме того, он играет большую роль в передвижении лимфы и тканевой жидкости, влияя тем самым на процессы восстановления и удаления продуктов обмена. Недостаточная работа «мышечного насоса» способствует развитию воспалительных процессов и образованию тромбов.

Таким образом нормальное состояние мышечной системы является важным и жизненно необходимым условием . Уровень состояния мышечной системы отражается показателем мышечной силы. Из этого следует, что для здоровья необходим определенный уровень развития мышц в целом и в каждой основной мышечной группе – мышцах спины, груди, брюшного пресса, ног, рук.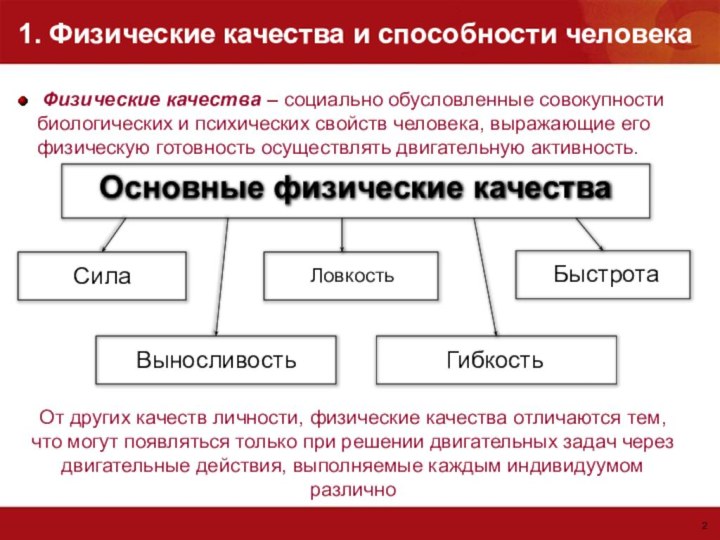

Развитие мышц происходит неравномерно как по возрастным показателям, так и индивидуально. Поэтому не следует форсировать выход на должный уровень у детей 7-11 лет. В возрасте 12-15 лет наблюдается значительное увеличение силы и нормативы силы на порядок возрастают. В возрасте 19-29 лет происходит относительная стабилизация, а в 30-39 лет – тенденция к снижению. При управляемом воспитании силы целесообразно в 16-18 лет выйти на нормативный уровень силы и поддерживать его до 40 лет.

Необходимо помнить, что между уровнем отдельных мышечных групп связь относительно слабая и поэтому нормативы силы должны быть комплексными и относительно простыми при выполнении. Лучшие тесты – это упражнения с преодолением массы собственного тела, когда учитывается не абсолютная сила, а относительная, что позволяет сгладить разницу в абсолютной силе, обусловленную возрастно-половыми и функциональными факторами.

Нормальный уровень силы – необходимый фактор для хорошего здоровья, бытовой, профессиональной трудоспособности.

Дальнейшее повышение уровня силы выше нормативного не влияет на устойчивость к заболеваниям и рост профессиональной трудоспособности, где требуется значительная физическая сила.

2. Методика и средства развития гибкости

Под гибкостью понимают способность к max по амплитуде движениям в суставах. Гибкость – морфофункциональное двигательное качество. Она зависит:

– от строения суставов;

– от эластичности мышц и связочного аппарата;

– от механизмов нервной регуляции тонуса мышц.

Различают активную и пассивную гибкость.

Активная гибкость – способность выполнять движения с большой амплитудой за счет собственных мышечных усилий.

Пассивная гибкость – способность выполнять движения с большой амплитудой за счет действия внешних сил (партнера, тяжести). Величина пассивной гибкости выше показателей активной гибкости.

В последнее время получает распространение в спортивной литературе термин “специальная гибкость” – способность выполнять движения с большой амплитудой в суставах и направлениях, характерных для избранной спортивной специализации. Под “общей гибкостью”, в таком случае, понимается гибкость в наиболее крупных суставах и в различных направлениях.

Кроме перечисленных внутренних факторов на гибкость влияют и внешние факторы: возраст, пол, телосложение, время суток, утомление, разминка. Показатели гибкости в младших и средних классах (в среднем) выше показателей старшеклассников; наибольший прирост активной гибкости отмечается в средних классах.

Половые различия определяют биологическую гибкость у девочек на 20-30% выше по сравнению с мальчиками. Лучше она сохраняется у женщин и в последующей возрастной периодике.

Время суток также влияет на гибкость, с возрастом это влияние уменьшается. В утренние часы гибкость значительно снижена, лучшие показатели гибкости отмечаются с 12 до 17 часов.

Утомление оказывает существенное и двойственное влияние на гибкость. С одной стороны, к концу работы снижаются показатели силы мышц, в результате чего активная гибкость уменьшается до 11%. С другой стороны, снижение возбуждения силы способствует восстановлению эластичности мышц, ограничивающих амплитуду движения. Тем самым повышается пассивная гибкость, подвижность увеличивается до 14%.

Неблагоприятные температурные условия (низкая температура) отрицательно влияют на все разновидности гибкости. Разогревание мышц в подготовительной части учебно-тренировочного занятия перед выполнением основных упражнений повышает подвижность в суставах.

Мерилом гибкости является амплитуда движений. Для получения точных данных об амплитуде движений используют методы световой регистрации: киносъемку, циклографию, рентгено-телевизионную съемку и др. Амплитуда движений измеряется в угловых градусах или в сантиметрах.

Средством развития гибкости являются упражнения на растягивания. Их делят на 2 группы: активные и пассивные. Активные упражнения:

– однофазные и пружинистые (сдвоенные, строенные) наклоны;

Физические величины: их использование в нашей повседневной жизни

Автор Анум
Последнее изменение 27-01-2023

Физические количества: Каждый день в нашей повседневной жизни мы имеем дело с измерениями и анализами. Пример физического количества: когда мы идем покупать фрукты или овощи, мы измеряем количество вещей, которые хотим купить, и соответственно платим за них. Это измеренное значение имеет номер и связанную с ним единицу измерения, например, \(3 \mathrm{~kg}\) манго, \(1 \mathrm{~kg}\) помидоров, \(500 \mathrm{~g }\) кориандр и т. д. Измерение помогает нам определить количество данного набора объектов.

Чтобы выразить это измерение, нам сначала нужна величина, чтобы связать все, что мы измеряем, и эти величины должны быть разными для разных видов измерений. Эти величины, которые помогают нам выразить измеряемую величину понятным для всех способом, известны как физические величины. Жизнь до появления этих физических величин была сопряжена с двусмысленностью, и выражение измерения нельзя было сделать однозначно, что приводило к путанице и хаосу.

Физическая величина может быть определена как характерное свойство системы, которое обычно измеряется количественно. Таким образом, мы можем выразить физическую величину как алгебраическое умножение произведения числового значения на его единицу.

Пример физической величины

Физическая величина, связанная с длиной, может быть записана как \(x\) \(\text {метр}\), где \(x\) — числовое значение, а \(\text { метр}\) указывает единицу измерения. Таким образом, все физические величины имеют по крайней мере два признака: числовой множитель и единицу измерения, в которой мы выражаем данное измерение.

Существует огромное количество явлений и объектов, которые мы изучаем в физике и технике. Они варьируются от крошечной продолжительности жизни атомного ядра до нынешнего возраста Вселенной, от диаметра амебы до диаметра Солнца, от энергии, необходимой для поднятия ручки, до энергии, высвобождаемой после ядерной реакции. , где малая и большая величины могут быть связаны друг с другом через миллионы степеней \(10\).

Числовые значения обеспечивают гораздо более глубокое понимание физических величин и уравнений, чем просто качественное описание. В зависимости от того, как эти величины описаны, физические величины можно разделить на:

Основные величины
Производные величины

Основные единицы физических величин

Единица физической величины может быть описана как стандарт, выбранный произвольно, который используется для оценки физических величин, относящихся к одному и тому же виду измерения. Поскольку физические величины могут быть незначительными или даже чрезвычайно большими, единицы измерения играют важную роль при написании выражения данного измерения. Хотя за прошедшие годы были разработаны различные системы единиц, во избежание путаницы была разработана международная система единиц или система СИ.

В отсутствие такой международно признанной системы ученым было трудно сравнивать физические величины и делиться своими открытиями за границей. Например, длину комнаты можно выразить в метрах, километрах, сантиметрах, футах и т. д. Эти единицы связаны друг с другом и могут быть преобразованы друг в друга; без таких четко определенных единиц было бы трудно выразить такое количество.

Фундаментальные величины

Физические величины, которые не зависят от других физических величин, называются Фундаментальными величинами. Они также известны как основные величины и используются для выражения других величин. Эти величины можно далее разбить и использовать для определения различных других физических величин. Основные величины:

Длина
Масса
Время
Электрический ток
Температура
Количество вещества
Сила света

9000 8 Дополнительные количества:

Плоский угол
Объемный угол

Основные единицы

Единицы которые связаны с фундаментальными величинами, известны как фундаментальные единицы. Это базовые единицы, которые не могут быть получены из других единиц и определяются с использованием международной системы единиц. Основные единицы: 9{5}\) состояние в Криптоне-\(86\). \(17\,\text {th}\) Генеральная ассамблея мер и весов в \(1983\) приняла новое определение метра. Это определение было дано в терминах скорости света. Таким образом, в настоящее время метр можно определить как расстояние, пройденное лучом света в вакууме за время, равное \(1/299 792 458\) секунды.

Второй – представлен \(\text {s}\). Это основная единица времени. Одна секунда определяется как длительность \(9192631770\) периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атомов цезия-\(133\).

{-2}\). 9{\ простое \ простое} \). Один радиан определяется как угол, образуемый дугой окружности, равной ее радиусу в центре.

Стерадиан — представлен \(\text {sr}\). Это основная единица телесного угла. Один стерадиан определяется как угол, образуемый в центре сферы единичного радиуса поверхностью, имеющей площадь, равную квадрату, длина стороны которого равна радиусу квадрата. Телесный угол сферы в ее центре равен \(4 \pi\) стерадиан.

Производные величины

Физические величины не могут быть определены сами по себе и могут быть разбиты на основные величины. Это зависимые величины. Производные физические величины выражаются через фундаментальные величины. Несколько примеров производных величин: сила, скорость, давление, объем, плотность и т. д.

Производные единицы

Единицы, полученные с использованием различных комбинаций основных единиц, называются производными единицами. Поскольку эти единицы получены с использованием базовых единиц, именно поэтому они известны как «производные» единицы. {-2}\). Который также известен как Ньютон (Н).

Как найти производную единицу величины

Шаг 1: Напишите формулу величины, единицу измерения которой вы хотите получить.
Шаг 2: Подставьте единицы измерения всех величин, участвующих в формуле.
Шаг 3: Все единицы величин должны быть записаны в одной выбранной системе единиц, предпочтительно в основной или стандартной форме.

Шаг 4: Выражение, содержащее все единицы, упрощается для вычисления последней единицы данной производной величины. Упростите производную единицу количества, чтобы вычислить ее окончательную единицу. 9{2}\).

Запись единиц физических величин

Перед записью единиц физических величин необходимо помнить о следующих правилах.

Правило 1 : Первая буква полного названия единиц никогда не должна начинаться с заглавной буквы, даже если единицы названы в честь ученого. Например, единица силы записывается как ньютон, единица мощности записывается как ватт, единица силы тока записывается как ампер, единица длины записывается как метр.
Правило 2 : Мы можем представить единицу физической величины, используя ее полное название или международно признанный символ.
Правило 3 : Всегда избегайте написания единиц во множественном числе. Это неверно. Например, \(10 \,\text {метр}\) правильно, но \(10 \,\text {метров}\) неверно, \(25 \mathrm{~kg}\) правильно, но \ (25 \,\mathrm{kgs}\) неверно.
Правило 4 : Мы никогда не добавляем точку или знак препинания в конце символа данной единицы измерения. Например, правильно \(10 \mathrm{~N}\), но \(10 \mathrm{~N}\). это неверно. 9{2}\)
Для измерения времени используются два прибора: Хронометр и Метроном . Время — единственная величина, имеющая одну и ту же единицу измерения (секунду) во всех системах единиц.

Резюме

Физическое можно определить как характерное свойство системы, которое обычно измеряется количественно. Таким образом, мы можем выразить физическую величину как алгебраическое умножение произведения числового значения на его единицу. Единица физической величины может быть описана как произвольно выбранный эталон, который используется для оценки физических величин, принадлежащих к тому же виду измерения.

Физические величины, которые не зависят от других физических величин, называются фундаментальными величинами. Они также известны как основные величины и используются для выражения других величин. Основными единицами измерения являются метр, килограмм, секунда, ампер, кандела, моль и кельвин. Физические величины не могут быть определены независимо и могут быть разбиты на базовые величины, называемые производными величинами. Это зависимые величины. Примерами производных величин являются сила, давление, ускорение, объем и т. д. Единицы выводятся с использованием различных комбинаций основных единиц, называемых производными единицами, например, ньютон, паскаль, метр в секунду и т. д.

Часто задаваемые вопросы о физических величинах

Ниже приведены часто задаваемые вопросы о физических величинах:

Q.1: Что такое основные единицы?
Ответ: Фундаментальные единицы – это единицы основных величин. Эти единицы являются независимыми и не могут быть разбиты на другие единицы.

Q.2: Что такое производные величины?
Ответ: Величины, которые не могут быть определены сами по себе и могут быть разбиты на основные величины, называются производными величинами.

Q.3: Что является единицей количества вещества?
Ответ: Моль — единица измерения вещества в системе СИ.

Q.4: Кандела является единицей СИ какой физической величины?
Ответ: Кандела — единица силы света в системе СИ.

Q.5: Вычислите единицу скорости.
Ответ: Скорость является производной физической величиной.
скорость \(=\frac{\text {расстояние}}{\text {время}}\)
\(\text {единица скорости в системе СИ} =\frac{\text {единица расстояния в системе СИ}}}{\text { СИ единица времени }}=\frac{m}{s}=\mathrm{m} / \mathrm{s}\)
Таким образом, единицей скорости в системе СИ является \(\mathrm{m} / \mathrm{s}\).

Узнайте об относительной плотности здесь

Мы надеемся, что эта статья о физических величинах поможет вам в подготовке. Оставьте свои вопросы в разделе комментариев, если вы застряли, и мы свяжемся с вами в ближайшее время.

Основы СИ: основные и производные единицы

Для простота понимания и удобство, дано 22 производных единицы СИ специальные имена и символы, как показано в таблице 3.

Производное количество	Имя	Символ	Выражение в терминах других единиц СИ	Выражение в пересчете на основных единиц СИ
Таблица 3. Производные единицы СИ со специальными названиями и символами
	Производная единица СИ
плоский уголок	радиан ^(а)	рад	—	м·м ^-1 = 1 ^(б)
угловой	стерадиан ^(а)	ср ^(с)	—	м ² · м ^-2 = 1 ^(б)
частота	герц	Гц	—	с ^-1
сила	ньютон	Н	—	м·кг·с ^-2
давление, напряжение	паскаль	Па	Н/м ²	м ^-1 ·кг·с ^-2
энергия, работа, количество теплоты	джоуль	Дж	Н·м	м ² ·кг·с ^-2
мощность, лучистый поток	Вт	Вт	Дж/с	м ² ·кг·с ^-3
электрический заряд, количество электричества	кулон	С	—	с·А
разность электрических потенциалов, электродвижущая сила	вольт	В	В/Д	м ² ·кг·с ^-3 ·А ^-1
емкость	фарад	Ф	С/В	м ^-2 ·кг ^-1 ·с ⁴ ·А ²
электрическое сопротивление	Ом		В/А	м ² ·кг·с ^-3 ·А ^-2
электропроводность	Сименс	С	А/В	м ^-2 ·кг ^-1 ·с ³ ·А ²
магнитный поток	вебер	ВБ	В·с	м ² ·кг·с ^-2 ·А ^-1
плотность магнитного потока	тесла	Т	Втб/м ²	кг·с ^-2 ·А ^-1
индуктивность	Генри	Х	Вб/А	м ² ·кг·с ^-2 ·А ^-2
Температура по Цельсию	градус Цельсия	°С	—	К
световой поток	люмен	лм	кд·ср ^(в)	m ² ·m ^-2 ·cd = cd
освещенность	люкс	лк	лм/м ²	m ² ·m ^-4 ·cd = m ^-2 ·cd
активность (радионуклида)	беккерель	Бк	—	с ^-1
поглощенная доза, удельная энергия (сообщенная), керма	серый	Гр	Дж/кг	м ² ·с ^-2
эквивалент дозы ^(d)	зиверт	Св	Дж/кг	м ² ·с ^-2
каталитическая активность	катал	кат		с ^-1 ·моль
^(а) Радиан и стерадиан можно выгодно использовать в выражениях для производных единицы для различения величин различной природы, но того же размера; некоторые примеры приведены в таблице 4. ^(б) На практике символы рад и ср используются там, где подходит, но производная единица «1» обычно опускается. ^(c) В фотометрии название единицы стерадиан и единица символ sr обычно сохраняется в выражениях для производных единиц. ^(d) Другие величины, выраженные в зивертах, относятся к окружающей среде эквивалент дозы, направленный эквивалент дозы, индивидуальный эквивалент дозы, и органная эквивалентная доза.

Для графической иллюстрации того, как 22 производные единицы со специальными именами а символы, приведенные в таблице 3, относятся к семи основным единицам СИ, см. отношения между единицами СИ.

Обратите внимание на градусы Цельсия. Производная единица в таблице 3 со специальным названием градус Цельсия и специальный символ °C заслуживает комментария. Из-за температуры пути шкалы, которые раньше были определены, остается обычной практикой выражать термодинамическую температура, символ T в части отличия от эталона температура Т ₀ = 273,15 К, ледяная точка. Эта температура разность называется температурой по Цельсию, символ t , и определяется количественным уравнением

т = т — т ₀ .

Единицей температуры по Цельсию является градус Цельсия, символ °C. числовое значение температуры по Цельсию

t /°C = T /K — 273,15.

Из определения t следует, что градус Цельсия равен по величине до кельвина, что, в свою очередь, означает, что численное значение заданной разности температур или температурного интервала, значение выражается в градусах Цельсия (°C) и равно числовое значение той же разницы или интервала, когда его значение выражается в единицах Кельвина (К).

Рубрики

Физические качества и их определения: Методика развития физических качеств Статьи

Физические способности человека и их развитие