Комплект для монтажа 2 солнечных модулей на наклонной крыше
Главная \ Солнечные панели (модули) \ Аксессуары для солнечных батарей \ Комплект для монтажа 2 солнечных модулей на наклонной крыше
Артикул: нет
- Описание
- Параметры
При помощи комплекта для монтажа 2-х солнечных батарей 200-390 Вт на наклонной крыше можно осуществлять монтаж солнечных батарей на крыше из металлочерепицы, на плоской оцинкованной кровле, на кровле из гибких гидроизоляционных материалов (шингласс и т.п.), на крыше из ондулина, шифера и профнастила.
Этот комплект крепежа рассчитан на монтаж трех панелей мощностью от 200 до 390 Ватт с толщиной рамы 35-45 мм.
Использование этого крепежного комплекта облегчает монтаж и обеспечивает вентиляцию задней части солнечных панелей, в результате чего снижается температура панелей, что в свою очередь, в летний период приводит к увеличению выдаваемой мощности.
Кроме этого монтажного комплекта, мы можем предложить различные варианты крепежа на любое количество солнечных панелей (для монтажа на крышу, на стену дома или на землю).
Базовая комплектация системы крепления солнечных панелей на скатную крышу на 2 солнечных модуля приведена в таблице.
| Наименование | Количество, шт |
| Направляющий профиль (анодированный алюминий) длина 2300 мм | 2 |
| Зажим концевой для СБ толщиной профиля 35-45 мм | 4 |
| Зажим центральный для СБ толщиной профиля 35-40 мм | 2 |
| L-образное крепления | 6 |
| Наличие на складе | да |
|---|---|
| Срок доставки | 2-3 дня |
теги:
Комплект для монтажа 2 солнечных модулей на наклонной крыше
Назад
Следуй за нами
В контакте
Новости27
04.2023
Повышение стоимости инверторов производства «Сибконтакт»
Мы вынуждены информировать Вас о повышение стоимости инверторов производства «Сибконтакт» со 2 мая 2023 года
подробнее.
..
27
04.2023
Поздравляем с наступающим праздником Труда и с Днем Победы!
Уважаемые друзья, ознакомьтесь с режимом работы магазина в праздничные дни.
подробнее…
23
03.2023
Скидка 10% на аккумуляторы VEKTOR ENERGY серии VRC (Карбон AGM)
До 31 марта действует дополнительная скидка 10% на аккумуляторы серии VRC.
подробнее…
22
02.2023
График работы магазина на День Защитника Отечества
Уважаемые друзья, ознакомьтесь с режимом работы магазина в праздничные дни
подробнее…
28
12.2022
Режим работы в новогодние праздники
Уважаемые друзья, ознакомьтесь с режимом работы магазина в праздничные дни
подробнее…
Наши партнеры
- B.B. Battery
- BINEOS
- Champion
- Fiamm
- FUBAG
- Generac
- Golden Motor
- Hiden
- HYUNDAI
- Must Power
- One Sun
- OSDA SOLAR
- SOFAR SOLAR
- SOLAR KERBEROS
- Sonnenschein
- TOPSOLAR
- VEKTOR ENERGY
- VOLTA
- Winston Battery
- YELLOW
- Восток
- Исток
- Лиотех
- НИП
- Полигон
- Сатурн
- Штиль
- ЭТК Энергия
Прибор для измерения коэффициента трения на наклонной поверхности COF-P01
Запросить консультацию
Страна производства:
КНР
Реализованные проектыПрибор для измерения коэффициента трения на наклонной поверхности COF-PO1 применяется для измерения статического коэффициента трения бумаги, картона, листов, конвейерных лент и других материалов.
Проверяя фрикционные свойства, во времени тестирования материалов, можно настраивать скорость открытия, упаковывания и другие параметры
Характеристики изделия
- Прибор позволяет определить статические коэффициенты трения образцов на наклонной поверхности
- Функции свободно изменяемой угловой скорости и автоматического восстановления изначального положения плоскости позволяет создавать нестандартные условия для испытаний
- Плоскость скольжения и блок скольжения размагничены и проверены на остаточную намагниченность, что значительно сокращает системные ошибки
- Прибор управляется микрокомпьютером с ЖК монитором, а так же имеет удобный интерфейс управления
- Оснащен портом RS232 для удобства передачи данных
- Поддерживает Систему Совместного использования данных Лаборатории — Lystem™ для единообразного и систематического управления данными
Стандарты
ASTM D202, ASTM D4918, TAPPI T815
Области применения
| Основная область применения | Пленки | Включая пластиковые пленки и листы, например PE, PP, PET, однослойные или многослойные композитные пленки и другие упаковочные материалы для еды и медикаментов |
| Бумага и картон | Различные виды бумаги и композитной полиграфической продукции из бумаги | |
| Расширенная область применения | Алюминиевые и кремниевые листы | Алюминиевые листы и кремниевые пластины |
| Тканые и нетканые материалы | Тканые и нетканые материалы, например мешки |
Технические характеристики
| Угол наклона | 0°~ 85° |
| Точность | 0. 01° |
| Угловая скорость | 0.1°/с~ 10.0% |
| Характеристика скольжения | 1300г(стандартно) 235г (опция) 200г (опция) Возможно изготовление на заказ |
| Условия тестирования | Температура: 23±2 °С Влажность: 20% RH ~ 70% RH |
| Габаритные размеры | 440 мм × 305 мм × 200 мм |
| Электропитание | AC 220 В 50 Гц |
| Вес | 20 кг |
Комплектация изделия
Стандартная комплектация
Прибор, микропринтер, блок скольжения 1300 г
По дополнительному заказу
Программное обеспечение, кабель связи, блок скольжения 235 г, блок скольжения 200 г и блок скольжения, изготовленный по заказу
Рекомендуем обратить внимание
Прибор для измерения коэффициента трения, отслаивания, модель C620H
Применяемые стандарты: ISO 8295, ISO 8510-2, ASTM D1894, ASTM D4917, ASTM D3330, TAPPI T816, TAPPI T549, GB 10006, GB/T 2790, GB/T 2791, GB/T 2792.
..
Подробнее
Прибор для измерения коэффициента трения, прочности на отслаивание, модель FPT-F1
Применяемые стандарты: ISO 8295, ISO 8510-2, ASTM D1894, ASTM D4917, ASTM D3330, TAPPI T816, TAPPI T549, GB 10006, GB/T 2790, GB/T 2791, GB/T 2792…
Подробнее
Прибор для определения коэффициента трения, модель MXD-02
Применяемые стандарты: ГОСТ 27492-87 (МЭК 648-79) , ISO 8295, ASTM D1894, TAPPI T816, GB 10006
Подробнее
Наклонные плоскости
Объект, помещенный на наклонную поверхность , будет часто скользить по поверхности. Скорость, с которой объект скользит по поверхности, зависит от того, насколько наклонена поверхность; чем больше наклон поверхности, тем выше скорость, с которой объект будет скользить по ней. В физике наклонная поверхность называется наклонной плоскостью. Известно, что объекты ускоряются вниз по наклонным плоскостям из-за неуравновешенной силы.
, действующих на любой объект, расположенный на наклонной плоскости, — сила тяжести и нормальная сила. Сила тяжести (также известная как вес) действует в направлении вниз; однако нормальная сила действует в направлении, перпендикулярном поверхности (на самом деле, нормаль означает «перпендикулярно»).
Первая особенность задач с наклонной плоскостью заключается в том, что нормальная сила равна , а не направлены в ту сторону, к которой мы привыкли. До этого момента в курсе мы всегда видели нормальные силы, действующие в восходящем направлении, противоположном направлению силы тяжести.
Задача определения результирующей силы, действующей на объект на наклонной плоскости, является сложной задачей, поскольку две (или более) силы не направлены в противоположные стороны. Таким образом, одну (или несколько) сил придется разложить на перпендикулярные составляющие, чтобы их можно было легко добавить к другим силам, действующим на объект. Обычно любую силу, направленную под углом к горизонтали, разлагают на горизонтальную и вертикальную составляющие. Однако это не тот процесс, который мы будем проводить с наклонными плоскостями. Вместо этого процесс анализа сил, действующих на объекты на наклонных плоскостях, будет включать определение весового вектора (F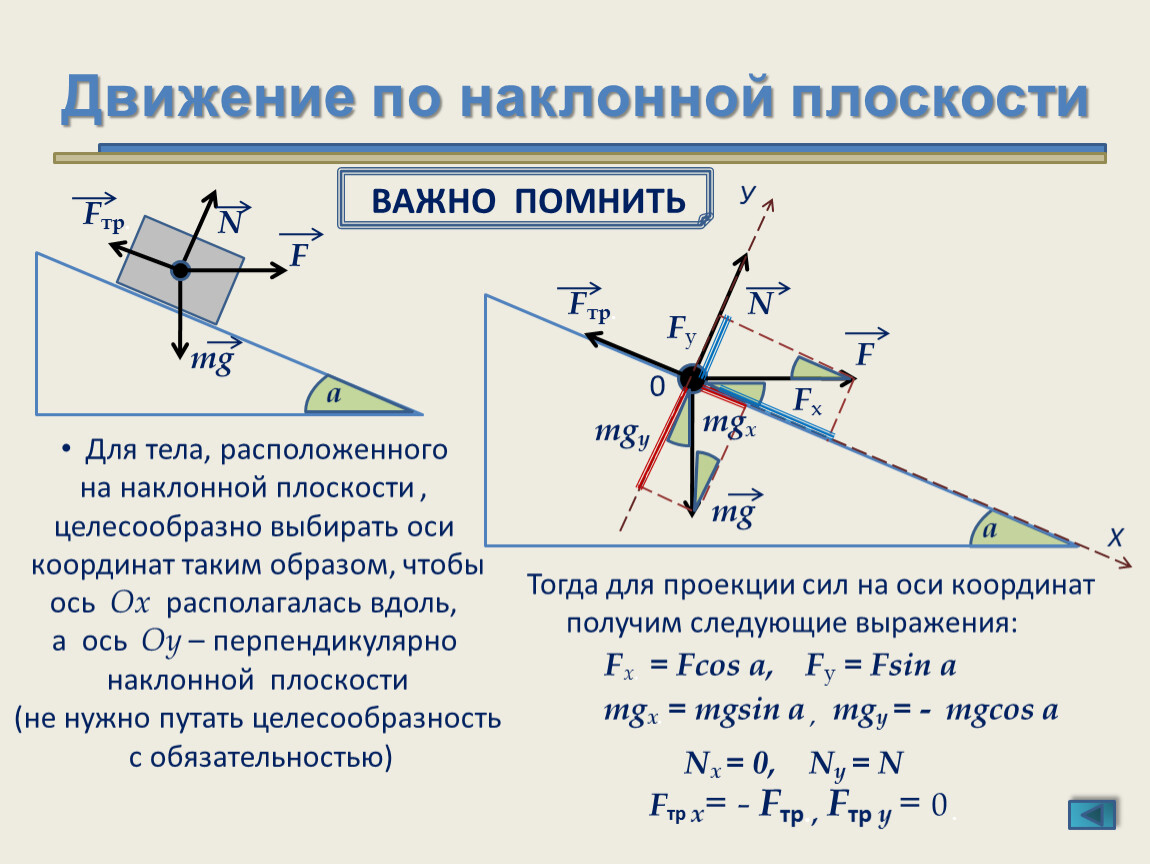 
Это вторая особенность задач наклонной плоскости. Сила тяжести будет разложена на две составляющие силы — одну, направленную параллельно наклонной поверхности, и другую, направленную перпендикулярно наклонной поверхности. На приведенной ниже диаграмме показано, как сила тяжести была заменена двумя составляющими — параллельной и перпендикулярной составляющей силы.
Перпендикулярная составляющая силы тяжести направлена против нормальной силы и, таким образом, уравновешивает нормальную силу. Параллельная составляющая силы тяжести не уравновешивается никакой другой силой. Этот объект впоследствии будет ускоряться вниз по наклонной плоскости из-за наличия неуравновешенной силы. Именно параллельная составляющая силы тяжести вызывает это ускорение. Параллельная составляющая силы тяжести является результирующей силой.
Задача определения величины двух составляющих силы тяжести — это простой способ использования уравнений.
Уравнения для параллельной и перпендикулярной составляющих:
При отсутствии трения и других сил (растяжения, приложенных и т. д.) ускорение объекта на наклонной поверхности равно значению параллельной составляющей (м *g*синус угла), деленное на массу (m). Это дает уравнение
(при отсутствии сил трения и других сил)
При наличии трения или других сил (приложенной силы, силы натяжения и т. д.) ситуация несколько усложняется. Рассмотрим схему, показанную справа. Перпендикулярная составляющая силы по-прежнему уравновешивает нормальную силу, поскольку объекты не ускоряются перпендикулярно наклону. Тем не менее, сила трения также должна учитываться при определении чистой силы. Как и во всех задачах о чистой силе, чистая сила представляет собой векторную сумму всех сил. То есть все отдельные силы складываются вместе как 9.
0003 векторов . Перпендикулярная составляющая и нормальная сила в сумме дают 0 Н. Параллельная составляющая и сила трения в сумме дают 5 Н. Суммарная сила равна 5 Н и направлена вдоль наклона к полу.
Приведенную выше задачу (и все задачи с наклонной плоскостью) можно упростить с помощью полезного приема, известного как «наклон головы». Задача о наклонной плоскости во всех отношениях похожа на любую другую задачу о результирующей силе, за исключением того, что поверхность была наклонена на градусов на градусов. Таким образом, чтобы преобразовать проблему обратно в более удобную для вас форму, достаточно наклонить голову в том же направлении, в котором был наклон наклонить . Или, что еще лучше, просто наклоните страницу бумаги (надежное лекарство от TNS — «синдром наклонной шеи» или «синдром тако-шейки»), чтобы поверхность больше не казалась ровной. Это показано ниже.
После того, как сила тяжести будет разделена на две составляющие и наклонена наклонная плоскость, задача должна выглядеть очень знакомо.
Просто игнорируйте силу гравитации (поскольку она была заменена двумя ее компонентами) и найдите результирующую силу и ускорение.
В качестве примера рассмотрим ситуацию, изображенную на диаграмме справа. На диаграмме свободного тела показаны силы, действующие на 100-килограммовый ящик, скользящий по наклонной плоскости. Плоскость наклонена под углом 30 градусов. Коэффициент трения между обрешеткой и склоном равен 0,3. Определить результирующую силу и ускорение ящика.
Начнем с вышеуказанной задачи, найдя силу тяжести, действующую на ящик, и компоненты этой силы, параллельные и перпендикулярные наклону. Сила тяжести равна 9.80 Н, а компоненты этой силы равны F параллельно = 490 Н (980 Н • sin 30 градусов) и F перпендикулярно = 849 Н (980 Н • cos30 градусов). Теперь нормальную силу можно определить равной 849 Н (она должна уравновешивать перпендикулярную составляющую вектора веса). Силу трения можно определить по величине нормальной силы и коэффициента трения; F трение составляет 255 Н (F трение = «mu»*F норма = 0,3 • 849 Н).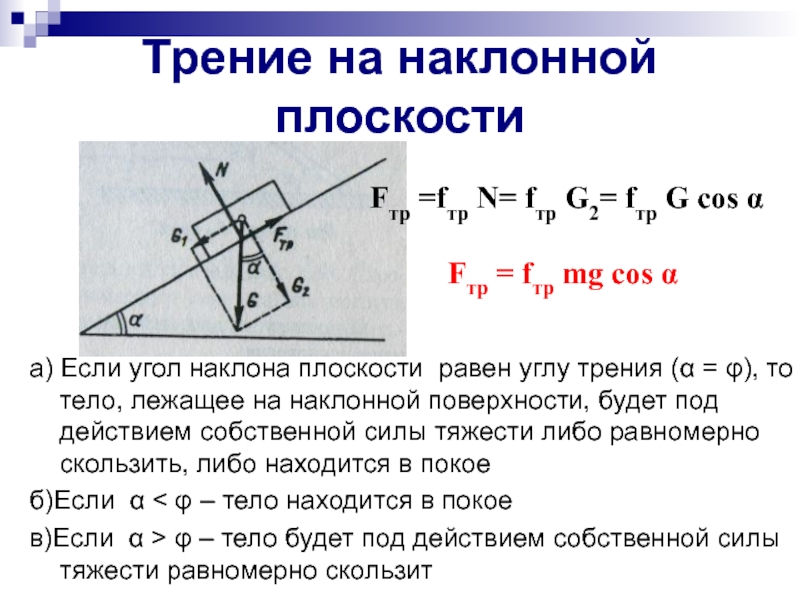
Чистая сила представляет собой векторную сумму всех сил. Силы, направленные перпендикулярно наклону, уравновешивают; силы, направленные параллельно наклону, не уравновешиваются. Чистая сила составляет 235 Н (490 Н — 255 Н). Ускорение составляет 2,35 м/с/с (F net /м = 235 Н/100 кг).
На двух приведенных ниже диаграммах показана диаграмма свободного тела для 1000-килограммовых американских горок при первом спуске двух разных аттракционов на американских горках. Используйте приведенные выше принципы векторного разрешения, чтобы определить результирующую силу и ускорение автомобилей американских горок. Предположим, что влияние трения и сопротивления воздуха пренебрежимо мало. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
Влияние угла наклона на ускорение американских горок (или любого объекта на склоне) можно наблюдать в двух вышеприведенных практических задачах.
С увеличением угла увеличивается ускорение объекта. Объяснение этого относится к компонентам, которые мы рисовали. По мере увеличения угла составляющая силы, параллельная наклону, увеличивается, а составляющая силы, перпендикулярная наклону, уменьшается. Именно параллельная составляющая вектора веса вызывает ускорение. Таким образом, ускорения больше при больших углах наклона. На приведенной ниже диаграмме показано это соотношение для трех различных углов возрастающей величины.
Немного физики американских горок
Американские горки вызывают два острых ощущения, связанные с начальным падением по крутому склону. Острые ощущения от ускорения создаются за счет использования больших углов наклона при первом падении; такие большие углы увеличивают значение параллельной составляющей вектора веса (составляющей, вызывающей ускорение). Ощущение невесомости производится за счет уменьшения величины нормальной силы до значений, меньших их обычных значений.
Используйте виджет ниже, чтобы исследовать другие ситуации с наклонной плоскостью. Просто введите массу, угол наклона и коэффициент трения (используйте 0 для случаев отсутствия трения). Затем нажмите кнопку Отправить , чтобы просмотреть ускорение.
Следующие вопросы предназначены для проверки вашего понимания математики и концепций наклонных плоскостей.
После того, как вы ответили на вопрос, нажмите кнопку, чтобы увидеть ответы.
1. Два мальчика играют в хоккей на соседней улице. Бродячая шайба движется по льду без трения , а затем поднимается по наклонной дороге без трения. Какая из следующих бегущих строк (A, B или C) точно изображает движение шайбы, когда она движется по ровной улице, а затем вверх по подъездной дорожке?
Объясните свой ответ.
2. Маленький Джонни стоит внизу подъездной дорожки и пинает футбольный мяч. Мяч катится на север по подъездной дорожке, а затем возвращается к Джонни. Какой из следующих графиков зависимости скорости от времени (A, B, C или D) наиболее точно отображает движение мяча, когда он катится вверх по подъездной дорожке и обратно?
Объясните свой ответ.
3. Мяч для гольфа катится по горизонтальному участку грина на 18-й лунке.
Затем он сталкивается с крутым нисходящим уклоном (см. Диаграмму). Участвует трение. Какой из следующих шаблонов бегущей строки (A, B или C) может быть подходящим представлением движения мяча?
Объясните, почему неуместные шаблоны неуместны.
4. Восьмой фрейм Мисси де Пенн в боулинг-лиге по средам стал катастрофой. Мяч скатился с полосы, прошел через грузовой люк в задней части здания, а затем по подъездной дорожке. Милли Митер (товарищ по команде Мисси), которая проводила каждую свободную минуту за подготовкой к экзамену по физике, начала визуализировать график зависимости скорости от времени для движения мяча. Какой из графиков зависимости скорости от времени (A, B, C или D) будет подходящим представлением движения мяча, когда он катится по горизонтальной поверхности, а затем вниз по склону? Рассмотрим силы трения.
5.
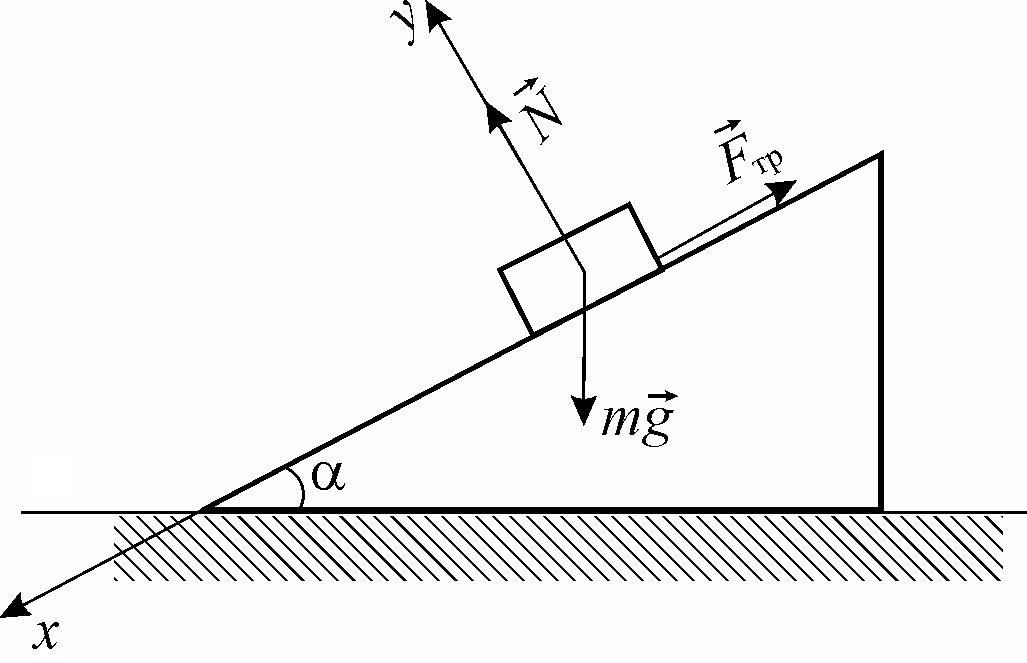Три партнера по лаборатории — Олив Н. Гленво, Глен Брук и Уоррен Пис — обсуждают задачу о наклоне (см. схему). Они спорят о значении нормальной силы. Олив утверждает, что нормальная сила равна 250 Н; Глен утверждает, что нормальная сила равна 433 Н; а Уоррен утверждает, что нормальная сила равна 500 Н. Хотя все три ответа кажутся разумными, правильным является только один. Укажите, какие два ответа неверны, и объясните, почему они неверны.
6. Лон Скейпер возится с газоном, когда из его тачки вырывается 2-килограммовая шина и начинает катиться вниз по крутому холму (уклон 30°) в Сан-Франциско. Нарисуйте параллельные и перпендикулярные компоненты этого весового вектора. Определить величину компонентов с помощью тригонометрических функций. Затем определите ускорение шины. Не учитывать силу сопротивления.
Наконец, определите, какой из графиков зависимости скорости от времени будет отображать движение шины при ее скатывании по склону.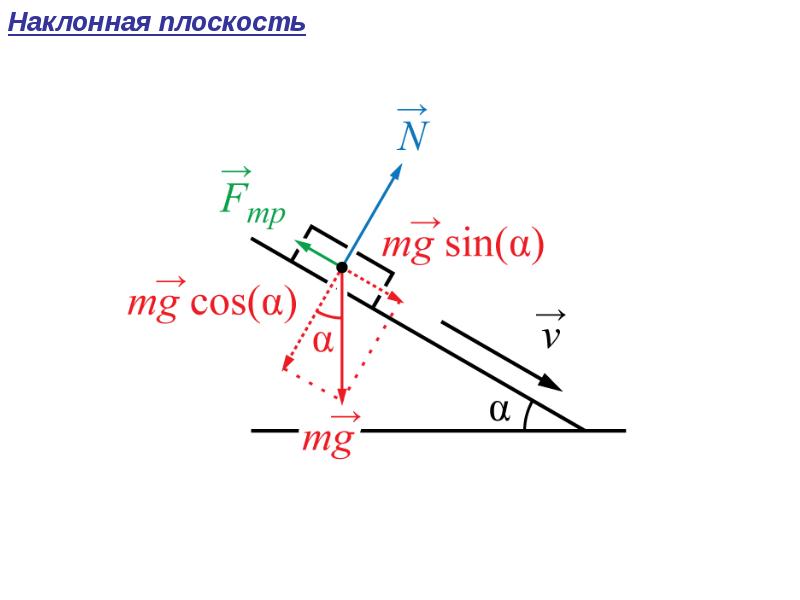
Объясните свой ответ.
7. На каждой из следующих диаграмм коробка массой 100 кг скользит по поверхности трения с постоянной скоростью 0,2 м/с. Угол наклона в каждой ситуации разный. Проанализируйте каждую диаграмму и заполните пропуски.
Следующий раздел:
Арифметика, математика и статистика — набор академических навыков
Наклонные плоскости (механика)
ContentsToggle Main Menu 1 Частица на наклонной плоскости 2 Рабочий пример: Частица, покоящаяся на наклонной плоскости наклонная плоскость 4 Проверь себя
Частица на наклонной плоскости
Для решения задач о частицах на наклонных плоскостях нам нужно найти силы, параллельные и перпендикулярные плоскости.
Если частицу массы $m$ положить на гладкую наклонную плоскость (т.е. сила трения $F=0$) и отпустить, то она скатится вниз по склону. Чтобы найти ускорение частицы при ее скольжении, разрешим направление движения. \begin{align} F & = ma, \\ mg \ \cos (9{\circ} — \theta) & = a, \\ g \ \sin (\theta) & = a. \end{align} Следовательно, поскольку $m$ сокращаются, мы видим, что масса частицы не влияет на ускорение, а влияет только угол наклона.
Если частицу массы $m$ поместить на шероховатую наклонную плоскость (т.е. сила трения $F \neq 0$), можно предотвратить скольжение частицы, если $F$ достаточно велика.
Разрешаем перпендикулярно плоскости (поскольку нормальная реакция $R$ действует под прямым углом к плоскости), где ускорение равно нулю. \begin{align} F & = ma, \\ R — mg \ \cos \theta & = m \times 0, \\ R & = mg \ \cos \theta. \end{align} Теперь разрешаем в направлении наклона, если частица покоится, то \begin{align} F & = ma, \\ mg \ \cos (9{\circ} — \theta) — F & = m \times 0, \\ mg \ \sin \theta & = F.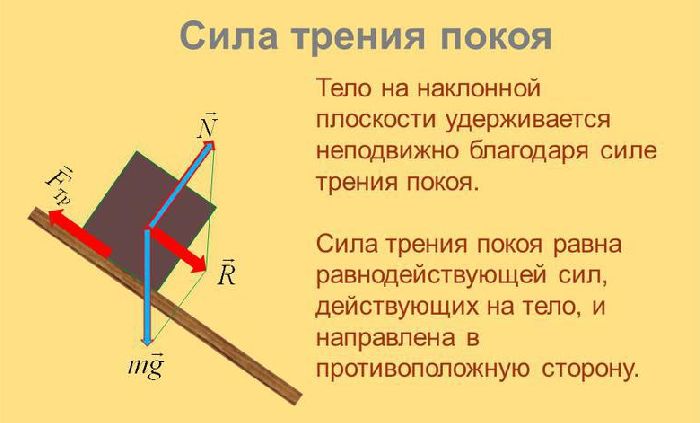
\end{align} где $F$ — сила трения, как показано на диаграмме. Мы знаем, что максимальная сила трения определяется выражением $F_{\text{MAX} } = \mu R$, поэтому \begin{align} F & \leq \mu R, \\ mg \ \\sin \theta & \leq \ mu мг \ \cos \theta, \\ \frac{ \sin \theta}{ \cos \theta} & \leq \mu, \\ \tan \theta & \leq \mu. \end{align} Следовательно, частица будет оставаться в покое до тех пор, пока $\tan \theta > \mu$, в этот момент она ускорится вниз по склону.
Рабочий пример: Частица, покоящаяся на наклонной плоскости
Нахождение ускорения
Частица массой $4 \mathrm{kg}$ находится в состоянии покоя на шероховатой поверхности, наклоненной к горизонтали под углом $\ theta$, где $\tan \theta = \frac{3}{4}$. Коэффициент трения между частицей и поверхностью $\mu=0,3$. Найдите ускорение частицы в момент отрыва.
Решение
Вы можете нарисовать диаграмму, подобную приведенной в разделе выше. По мере движения частицы ($\tan\alpha\geq\mu$) трение будет иметь максимальное значение $F_{\text{MAX} } = \mu R$ и будет действовать в направлении, противоположном ускорению (которое действует вниз по склону по мере скольжения частицы).
