Как массу посчитать: Как рассчитать массу и объем, если известна плотность песка?

13.04.2023 0 Разное

Содержание

Как посчитать вес металла по размерам − формулы массы

При составлении сметы строительства или демонтажа металлоконструкций, покупке металлопроката или подготовке металлолома к сдаче, для найма подъемных механизмов бывает необходимо вычислить массу и количество металла, вес лома.

Как это сделать

Для получения необходимой информации можно обратиться к справочникам, и они рассчитают теоретический вес. Второй вариант – воспользоваться помощью калькулятора расчета веса металла по размерам. Если нет под рукой Интернета, есть простой выход – использовать школьные формулы вычисления массы по объему и плотности.

По справочникам

Сборник справочных материалов содержит таблицы металлов, по которым легко определить вес металлопроката любого вида, из черного и цветного металлов или сплавов. Кроме этого, в сборнике приведены формулы, чтобы посчитать вес металла по размерам для заготовок различных конфигураций, данные по удельному весу металлов.

К справочнику приходится обращаться при самостоятельном произведении математических расчетов, например, к таблице плотности металлов. Чтобы вычислить массу детали из цветного металла, понадобится переводной коэффициент.

С готовой таблицей легко самостоятельно рассчитать вес листа металла. По данной толщине и марке стали находится теоретический вес 1 м2, искомая величина умножается на площадь листа. Особенно это удобно для стали с рифлением, выступами, цинковым напылением, учитывается также способ прокатки (холодный или горячий).

Упрощается просчет массы швеллера и двутавра – изделий со сложным сечением. Для них есть таблица с указанием номера профиля и соответствующего веса 1 пог. м в кг. Не нужно заморачиваться, чтобы вычислить вес стальной арматуры, к тому же в таблице указано количество погонных метров в 1 т.

Аналогичные таблицы существуют для металлических профилей Г-образного сечения: указан вес 1 м уголка для конкретной толщины и ширины полки. Правда, такие расчеты отличаются от фактического веса, так как таблицы составлены на основе ГОСТа. В реальности же прокат не всегда соответствует государственным стандартам.

Плотность стали зависит от температурных показателей. Все табличные данные соответствуют температуре 20°C. Данное замечание не относится к цветному прокату.

По калькулятору

Посчитать вес металла по размерам можно онлайн либо скачать калькулятор на компьютер (смартфон). Это удобный вид расчета, потому что не нужно перелистывать справочники в поисках нужных таблиц – достаточно задать конкретные параметры. С помощью калькулятора определяют вес железа любой марки и конфигурации с точностью до сотых долей:

  • арматуры, прутков;
  • листового проката;
  • шестигранников, кругов, квадратов;
  • труб;
  • плит;
  • уголков, швеллеров, двутавров.

Существуют также калькуляторы для цветного проката и для определения объемного веса металла, который важно знать для грузоперевозок.

Алгоритм работы с калькулятором простой:

  1. Выбирается тип проката, вид изделия и марка металла.
  2. Заносятся результаты замеров.
  3. Нажимается кнопка «Посчитать».

Особенно удобна калькуляция для изделий с нестандартной и сложной формой. Кроме того, можно определять метраж изделия по его весу, т.е. переводить килограммы в метры.

Расчет веса по математическим формулам

Вес любого изделия находится так: M = ρV (ρ – плотность, V – объем изделия) или по формуле массы через площадь сечения: M = ρSL (S — площадь сечения, L — длина). Для углеродистой стали принято использовать усредненное значение ρ, равное 7850 кг/м3 или 0,00785 г/мм3, либо 7,85 г/см3 (в зависимости от выбранных единиц измерений). Самое простое вычисление – это масса стального куба со стороной 1 м. Она равна 7850 кг, или 7,85 т.

Различают практические и теоретические формулы массы. Первые адаптированы к определенным условиям, чтобы облегчить и ускорить расчеты.

Листовой прокат

Для расчета веса листового металла нужно перемножить 3 измерения – длину, ширину и толщину изделия, полученный результат умножить на плотность металла. Например: длина проката 1 м, ширина – 2 м, толщина – 2мм, тогда M = 1×2×0,002×7850 = 31,4 (кг).

При определении массы нескольких одинаковых листов железа, достаточно рассчитать вес 1 листа и умножить на количество.

Пруток, проволока и арматура

Для определения массы прутка или любого изделия круглого сечения, используется такая теоретическая формула: M= πR2Lρ, где L – длина, R – радиус заготовки, π = 3,14, ρ – плотность металла. Другая, практическая, формула: M = (0,02466R2)L. Ее можно использовать и для рифленой арматуры.

Из объема найти массу прямоугольного прутка совсем просто. Нужно перемножить длину, ширину и толщину (это объём V), затем найти в справочнике соответствующую плотность и умножить ее на V: M = ABLρ, где A, B – ширина и толщина.

Круг

Чтобы найти вес металлического круга, нужно подставить числовые значения в формулу: M = πR2dρ (R– радиус, d – толщина).

Шестигранный пруток

Лучше всего обратиться за помощью к готовым таблицам, но в их отсутствии расчеты можно произвести самостоятельно:

M = (3√3/2)а2Lρ,

где а – длина стороны шестигранника (мм), L – длина прутка (мм), ρ = 0,00785 г/мм3.

Прямоугольный профиль

Узнать массу прямоугольной профильной трубы можно так:

M = 2(a+b)sLρ,

где a и b – ширина и высота сечения (мм), s – толщина стенки (мм), L – длина трубы (мм), ρ = 0,00785 г/мм3 . Если стенки разной толщины, проводится несколько измерений и находится среднее значение.

Масса круглой трубы

Посчитать вес металла по размерам в данном случае можно по следующим формулам:

M = π(R2 – r2)Lρ, M = 2πRsLρ, M = (D-s)s×0,2466

где М – масса, R2 – внешний радиус, r2 – внутренний радиус, L – длина трубы, ρ. – плотность стали, s – толщина стенки, 0,2466 – константа, соответствующая плотности углеродистой стали ρ = 7,85 г/см3.

Трубу с закрытым концом можно рассматривать как бочку и применить для нахождения ее веса представленные выше формулы для трубы и круга.

Вес фигурных изделий

Посчитать массу, зная объем и плотность, можно для изделий любой конфигурации. Нужно только правильно вычислить объем и подставить значение в известную формулу M = Vρ.

Объем пирамиды рассчитывается по формуле: V = 1/3 SH, где S – площадь основания, H – высота пирамиды.

Для усеченной пирамиды V = 1/3 h(F + f + √Ff), где F и f – площади большего и меньшего основания.

Объем цилиндра: V = πR2H.

Объем конуса: V = 1/3 πR2H, объем усеченного конуса: V = 1/3 πH(R2 + Rr + r2), где H – высота, R и r – радиусы большего и меньшего основания.

Объем шара: V = πD3/6 (D – диаметр).

Для уголка: V = s(h1 + h2)L, где L – длина уголка, s – толщина металла, h1 и h2 – ширина полок.

Объем изделия витиеватой формы и небольших габаритов находят по количеству вытесненной жидкости, поместив его в емкость с водой.

Если конструкция изготовлена из разных металлов и сплавов, тогда можно найти ее массу через вес отдельных деталей.

Теоретический вес рассчитывается по формулам, практический (фактический) определяется взвешиванием. Естественно, что всегда между этими величинами будет несоответствие. Расчет массы заготовки, произведенный самостоятельно по математическим формулам, также может отличаться от табличных или же выданных калькулятором.

Для получения более точных результатов целесообразно пользоваться данными справочников или электронных вычислительных устройств.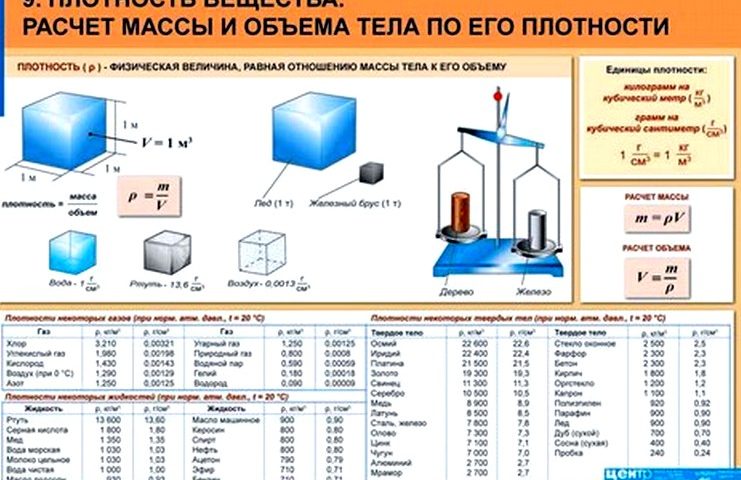

Формулы для вычисления массы тел различной формы

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

1.
Масса параллелепипеда (бруска)

Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:

2. Масса цилиндра

Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:

3. Масса шара

Объем шара: , где — диаметр шара.
Тогда масса:

4. Масса сегмента шара

Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:

5. Масса конуса

Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:

6. Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:

7. Масса пирамиды

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:

8. Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием (, ) формула выглядит проще:

 вычисление массы

Что такое масса? — Определение, единицы, формула и примеры

 

Массу лучше всего понимать как количество материи, присутствующей в любом объекте или теле. Все, что мы видим вокруг себя, имеет массу. Например, стол, стул, ваша кровать, футбольный мяч, стакан и даже воздух имеют массу. При этом все объекты легкие или тяжелые из-за своей массы. На этом уроке мы узнаем, что такое масса, как ее вычислить, и ее примеры, открывая при этом интересные факты о ней.

1. Что такое масса?
2. Что такое единица массы?
3. Разница между массой и весом
4. Часто задаваемые вопросы по Mass

Что такое масса?

В физике масса — это основное свойство материи и одна из фундаментальных величин.

Масса определяется как количество вещества, присутствующего в теле. Единицей массы в системе СИ является килограмм (кг). Формулу массы можно записать так:  

Масса = Плотность × Объем

Примечание : Масса тела постоянна; он не меняется в любое время. Только в определенных крайних случаях, когда от тела отдается или отнимается огромное количество энергии, масса может воздействовать. Например, при ядерной реакции крошечное количество вещества превращается в огромное количество энергии, это уменьшает массу вещества.

Что такое единица массы?

Существуют различные единицы измерения массы, такие как килограммы, граммы, фунты, фунты и т. д., но единицей массы в системе СИ является «килограмм» или кг. Каждая единица массы может быть преобразована в другие единицы с помощью соответствующей формулы преобразования, не затрагивающей смысла и сути измеряемой величины.

Примечание. 1 кг равен 2,20462 фунта.

Разница между массой и весом

Люди часто путают массу и вес, и в конечном итоге используют эти два термина как синонимы. Однако масса и вес — это два разных термина, и важно понимать разницу между ними. Разница между массой и весом показана в приведенной ниже таблице.

.
  Масса Вес
Определение Масса определяется как количество вещества в веществе Вес определяется как количество силы, действующей на массу объекта из-за ускорения под действием силы тяжести.
Обозначение Масса представлена ​​буквой «М».

Масса представлена ​​буквой «W».

Формула •Масса тела всегда постоянна.
• Один из способов расчета массы: масса = объем × плотность.		 •Вес является мерой гравитационной силы, действующей на массу.
• Формула веса: Вес = масса × ускорение свободного падения
Единица измерения Единицей массы в СИ является «килограмм».   Единицей веса в системе СИ является Ньютон (Н).
Количество Тип •Масса является базовой величиной.
• Масса имеет только величину и, следовательно, это скалярная величина		 •Вес является производной величиной.
• Вес имеет как величину, так и направление (к центру тяжести) и, следовательно, является векторной величиной.
Измерительный прибор Массу можно легко измерить с помощью любых обычных весов.
Например, балочный баланс, рычажный баланс, панорамный баланс и т. д.		 Вес можно измерить с помощью пружинных весов или по приведенной выше формуле.

Знаете ли вы, что у нас разный вес на Земле, на Луне и в космосе? Однако наша масса везде одинакова.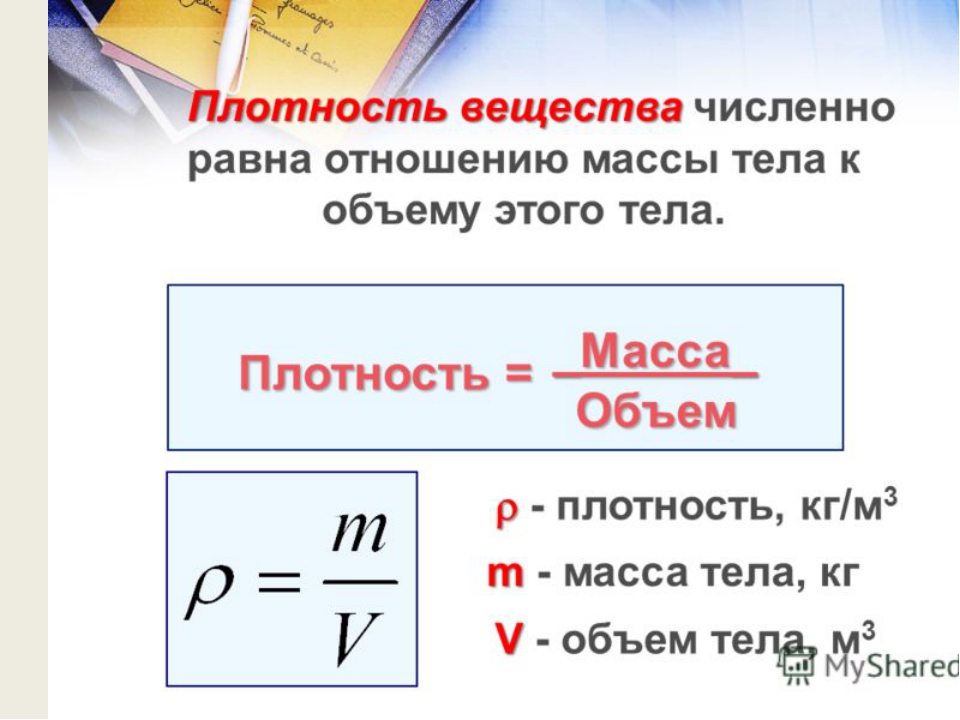

Теперь давайте посмотрим на некоторые важные факты, связанные с массой:

  • Масса имеет только величину, следовательно, это скалярная величина.
  • Вес имеет как величину, так и направление; это векторная величина.
  • Массу также можно определить как «энергию, запасенную в частицах».
  • Масса представляет собой общее количество атомов или частиц, которые оно содержит.

 

  1. Пример 1: Сэм на Земле весит 1000 фунтов. На какой-нибудь другой планете вес Сэма составил бы 38 % от земного. Сколько бы Сэм весил на этой планете?
    Решение: Мы знаем, что вес Сэма на Земле составляет 1000 фунтов, а его вес на другой планете будет составлять 38 % от земного. Следовательно, вес Сэма на другой планете = 38 % × его вес на Земле = 0,38 × 1000 фунтов = 380 фунтов

  2. Пример 2: Масса объекта составляет 6000 фунтов. Вычислите его массу в тоннах.
    Решение: Мы знаем, что 1 тонна = 2000 фунтов. Таким образом, 6000 фунтов = 6000/2000=3 тонны.

  3. Пример 3: У Дамиана есть книга массой 2,2 кг. Каков вес книги на Земле?

    Решение:

    Масса учебника = 2,2 кг, ускорение свободного падения = 92\)

    Вес учебника = 21,56 Н

    Следовательно, вес учебника на Земле равен 21,56 Н.

 

перейти к слайду

перейти к слайдуперейти к слайдуперейти к слайду

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, зачем нужна математика, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

 

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы по Mass

Имеет ли воздух массу?

Да, воздух имеет массу. Например, надутый воздушный шар весит тяжелее, чем сдутый воздушный шар, что доказывает, что воздух внутри надутого воздушного шара имеет массу.

Масса и объем одинаковы?

Масса – это количество материи, из которой состоит объект. Объем — это количество свободного места, которое занимает объект. Следовательно, масса и объем не совпадают.

Плотность и масса — одно и то же?

Масса измеряет количество вещества, присутствующего в веществе. Плотность показывает количество вещества в данном пространстве для вещества. Плотность и масса могут быть такими же, как единица объема.

Вес и масса — одно и то же?

Нет, вес и масса не одно и то же. Вес – это сила, действующая на тело, а масса – это количество вещества в теле. Вес может изменяться в зависимости от силы, в то время как масса постоянна.

Что такое единица массы S.I?

Единицей массы в системе СИ являются килограммы (кг).

Что такое формула массы?

Формула, используемая для расчета массы объекта: Плотность × Объем.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист массы

Калькулятор массы

Это базовый калькулятор массы, основанный на плотности и объеме. Этот калькулятор принимает и генерирует результаты многих общих единиц.


Что такое масса?

Масса обычно определяется как количество материи внутри объекта. Чаще всего его измеряют как инерционную массу, включающую сопротивление объекта ускорению при заданной некоторой результирующей силе. Однако материя определяется в науке довольно свободно и не может быть точно измерена. В классической физике материя — это любое вещество, имеющее массу и объем.

Количество массы объекта часто коррелирует с его размером, но объекты большего объема не всегда имеют большую массу. Например, надутый воздушный шар будет иметь значительно меньшую массу, чем мяч для гольфа, сделанный из серебра. Хотя во всем мире для описания массы используется множество различных единиц, стандартной единицей массы в Международной системе единиц (СИ) является килограмм (кг).

Существуют и другие общие определения массы, включая активную гравитационную массу и пассивную гравитационную массу. Активная гравитационная масса — это мера того, насколько сильно гравитационная сила действует на объект, а пассивная гравитационная масса — это мера гравитационной силы, действующей на объект в пределах известного гравитационного поля. Хотя они концептуально различны, не было проведено убедительных и однозначных экспериментов, которые продемонстрировали бы существенные различия между гравитационной и инертной массой.

Масса и вес

Слова «масса» и «вес» часто используются взаимозаменяемо, но хотя масса часто выражается путем измерения веса объекта с помощью пружинных весов, они не эквивалентны. Масса объекта остается постоянной независимо от того, где находится объект, и, следовательно, является внутренним свойством объекта. С другой стороны, вес изменяется в зависимости от гравитации, поскольку он является мерой сопротивления объекта его естественному состоянию свободного падения.

Сила тяжести на Луне, например, примерно в шесть раз меньше, чем на Земле, из-за ее меньшей массы. Это означает, что человек с массой 70 кг на Земле будет весить примерно одну шестую своего веса на Земле, находясь на Луне. Однако их масса на Луне все равно составляла бы 70 кг. Это соответствует уравнению:

Ф =33
Гм 1 м 2
р 2

В приведенном выше уравнении F — сила, G — гравитационная постоянная, m 1 и m 2 — масса Луны и объекта, на который она действует. r — радиус Луны. В обстоятельствах, когда гравитационное поле постоянно, вес объекта пропорционален его массе, и нет проблем с использованием одних и тех же единиц для выражения обоих.

В метрической системе вес измеряется в ньютонах по уравнению Вт = мг , где Вт — вес, м — масса, а г — ускорение, вызванное гравитационным полем.

Вам так же может понравиться...

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *