Какие упражнения выполнять для развития трапеции: 6 лучших упражнений на трапецию

6 лучших упражнений на трапецию

Прокачиваем трапецию: особенности анатомии мышцы и эффективные упражнения Назад к новостям

Развитие трапециевидных мышц важно для того, чтобы плечевой пояс смотрелся гармонично. У некоторых спортсменов при умеренной нагрузке рост трапеции соразмерен росту мышц спины и плеч, но бывают и случаи, когда при очень интенсивных нагрузках трапеция растет слабо, и возникает визуальный дисбаланс. Сегодня мы разберемся в особенностях трапециевидных мышц и в том, какие упражнения подойдут для их проработки.

Поговорим об анатомии трапеции

Трапециевидная мышца находится в верхней части спины и примыкает к шейным мышцам. Визуально она делится на три основных части:

• Верхняя – примыкает к мышцам шеи и отвечает за поднимание плеч вверх;
• Средняя – проходит между лопаток и поднимает их;
• Нижняя – опускает лопаточные кости.

Поддержка трапеции в тонусе важна для любого спортсмена, так как она повышает силовой результат, снимает часть нагрузки на плечевые суставы и связки, снижает искривленность позвоночника в шейном отделе и уменьшает риск получения травмы плечевого пояса.

Несколько важных рекомендаций по тренировке трапеции

1. Шраги считаются оптимальным типом упражнений, но их надо выполнять правильно, не затрагивая бицепсы и предплечья. Локти должны быть практически полностью прямыми в течение подхода;
2. Выбирайте не слишком большой вес снаряда, но работайте в полную амплитуду, чтобы чувствовать максимальное сокращение мышц в верхней точке и задерживаться в ней на одну-две секунды;
3. Трапеции подходит пампинг – делайте суперсеты, чтобы наполнить мышцы кровью, или делайте дропсеты в конце каждого подхода;
4. Тренировать трапецию достаточно раз в неделю, так как это небольшая группа мышц;
5. Лучше проводить короткую, но интенсивную тренировку из одного-двух упражнений с чередованием на каждой тренировке в разном порядке;
6. Во время тренировки держите спину прямо;
7. Не вращайте суставами плеч при выполнении шрагов.

Эффективные упражнения для прокачки трапеции

• Шраги со штангой. 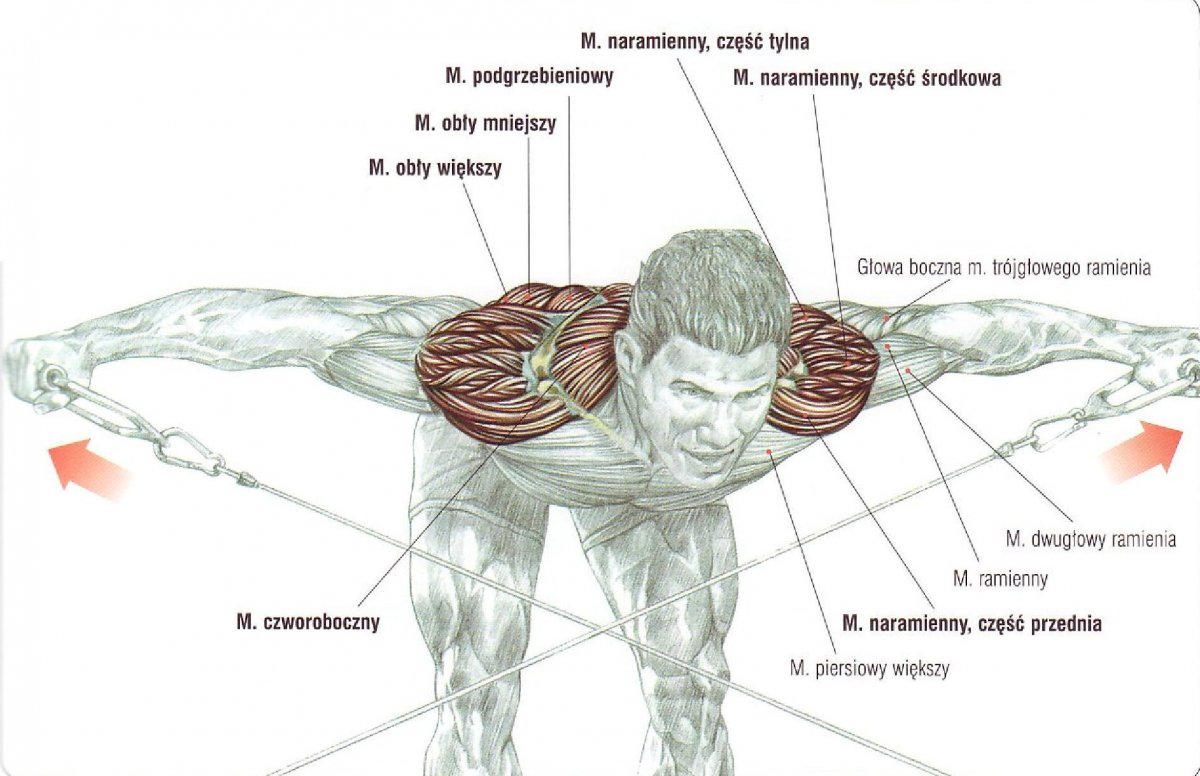Это упражнение для повышения массы мышцы, так как задействуется ее верхняя часть – штанга при подъеме располагается перед вами. Движения выполняются амплитудно, будто в верхнем положении вы пытаетесь коснуться ушей плечами. Упражнение позволяет использовать довольно высокие веса, можно также применять кистевые лямки и атлетические пояса. Хват должен быть средним, ниже плеч, чтобы не задействовать их.
• Шраги с гантелями. Они также прорабатывают верхнюю часть трапеции, но вес нужно выбирать поменьше, чтобы сделать больше повторений – это дает эффективный пампинг. Кисти располагаются параллельно друг другу, задействуются предплечья. Руки должны быть прямыми, локти не стоит сгибать, тогда подъем снаряда будет происходить за счет трапеции.
• Шраги на тренажере. Для этого нужен нижний блок и широкая рукоять. Спину необходимо держать прямо, плечи подтягиваются вверх и немного назад, чтобы нагрузи среднюю часть трапеции, а также растянуть нижнюю часть.
• Упражнения со штангой за спиной. Они помогают проработать среднюю и нижнюю часть трапеции, но требуют хорошей растяжки суставов и крепкого мышечного каркаса, поэтому не подходят новичкам. Удобнее всего выполнять подходы на тренажере Смита. В нижней точке расслабляются все мышцы плечевого пояса, но поясничный отдел позвоночника при этом должен оставаться ровны. Чем ближе к спине держится штанга, тем лучше работает трапеция.
• Тяга к подбородку со штангой на узком хвате. Это базовый тип упражнения, который задействует плечи и трапеции. Хват может быть достаточно узким, локоть можно держать выше кисти, чтобы работать в полную амплитуду. Чем шире будет хват, тем больше нагрузка будет уходит на средние дельты.
• Становая тяга. Любая становая тяга дает динамическую нагрузку на остальные мышцы и статическую – на трапецию, что очень важно для ее роста.

Надеемся, эта информация будет вам полезна! Также мы предлагаем большой выбор запчастей для спортивных тренажеров как в залах, так и для домашних устройств. Мы выполняем качественный ремонт и обслуживание тренажеров. Если вы – владелец тренажерного зала, также у нас вы можете купить шкафчики и скамьи для раздевалки.

Забытые мышцы. Какие тренировки помогут добиться идеальной фигуры :: Лайфстайл :: РБК Спорт

adv.rbc.ru

adv.rbc.ru

adv.rbc.ru

Спорт

Телеканал

Pro

Инвестиции

Мероприятия

РБК+

Новая экономика

Тренды

Недвижимость

Спорт

Стиль

Национальные проекты

Город

Крипто

Дискуссионный клуб

Исследования

Кредитные рейтинги

Франшизы

Газета

Спецпроекты СПб

Конференции СПб

Спецпроекты

Проверка контрагентов

РБК Библиотека

Подкасты

ESG-индекс

Политика

Экономика

Бизнес

Технологии и медиа

Финансы

РБК Компании

adv. rbc.ru

adv.rbc.ru

Трапеция и предплечья — те две группы мышц, которым не всегда уделяют внимание на тренировках, но без них не получится развития гармоничной фигуры. Какие упражнения и как их следует выполнять для роста этих мышц — в материале «РБК Спорт»

Читайте нас в

Новости

Тренировка трапеции (Фото: Lars Baron/Getty Images)

Мышцы трапеции являются вершиной развитого корпуса человека. Если они недостаточно проработаны, то визуально фигура атлета выглядит неполной. Несмотря на то что трапеция находится в постоянной нагрузке в нашей повседневной жизни, она от этого автоматически не растет в объемах. Поэтому необходимо включать упражнения на ее развитие в свой тренировочный цикл. Как правило, эти упражнения можно совмещать с тренировкой мышц спины или плеч.

Анатомически трапеция расположена вверху спины и как бы соединяет плечи с шеей. Сама мышца состоит из трех частей:

• верхняя часть соединена с шеей, ее задача — обеспечивать подъем плеч вверх;
• средняя часть расположена между лопаток и, соответственно, обеспечивает их подъем;
• нижняя часть расположена внизу лопаток и отвечает за их опускание.

adv.rbc.ru

Тренировка трапеции позволит не только развить саму мышцу, но и положительно скажется на выполнении базовых упражнений, в которых она участвует.

Упражнения для тренировки трапеции:

1. Базовое упражнение на трапецию — это пожимание плечами в положении стоя — выполните один подход, отдохните 30 секунд, не выпуская гантели из рук, и выполните второй подход.
2. Далее переместитесь на наклонную скамью (угол приблизительно в 45 градусов) и выполняйте тяговые движения вверх — здесь важно не поднимать гантели, а именно тянуть их.
3. Тяга штанги перед собой с короткой амплитудой в положении стоя. Хват штанги — чуть шире плеч. Выполняйте тяговые движения в короткой амплитуде движения — примерно так, чтобы гриф доходил до уровня поясницы.

Рекомендуется выполнять эти упражнения по системе суперсета, то есть одно за другим, так как трапеция требует именно интенсивной нагрузки.

Мышцы предплечий находятся между кистью и локтевым суставом и участвуют в работе других мышц, а самостоятельно практически не используются. Это связано с тем, что они имеют свойство сопротивления в нагрузке, а значит, и тренировать их нужно с особой тщательностью и интенсивностью (не менее трех подходов, в каждом из которых следует выполнять не менее 15 повторов). Как правило, тренировка предплечий совмещается с тренировкой мышц рук.

Упражнения для тренировки предплечий

1. Возьмите в руку гантель и положите руку на скамью таким образом, чтобы предплечье лежало на поверхности, а кисть при этом свешивалась. Начинайте движения кистью из нижнего положения вверх.

2. Переверните руку на скамье и продолжайте выполнять аналогичное движение.

Выполните подряд два суперсета из данных упражнений. Как вариант: гантели можно заменить штангой.

Автор

Александр Бархаев

Читайте нас в

Новости

adv.rbc.ru

adv.rbc.ru

adv.rbc.ru

Тестирование трапеции | Лучший мир благодаря лучшему программному обеспечению

29 марта 2017 г.

процесс

Замена тестовой пирамиде.

Многие из нас знакомы с пирамидой испытаний — видением всех испытаний, устроенных их родственником число. Например, сообщение в тестовом блоге Google Просто скажите «нет» большему количеству сквозных тестов показывает следующую пирамиду

• малые тесты Основание пирамиды сформировано малыми модульными тестами. Их очень много; они просты в написании и быстро запускаются. Модульные тесты проверяют отдельные фрагменты кода изолированно, обычно пытаясь охватить все. пути кода и пограничные случаи.
• средние тесты Средний слой в пирамиде занят тестами, которые пытаются поставить несколько части вместе. Эти тесты интегрируют фрагмент кода в более крупную систему. Некоторые части над системой издеваются; например, мы можем протестировать функцию ведения журнала, издеваясь над базой данных.
• большие тесты На вершине пирамиды лежат сквозные тесты (также называемые функциональными тестами). Их сложно написать, они требуют времени для запуска и могут охватывать только некоторые пути выполнения. Я также считаю, что тесты e2e трудно рефакторить; они замедляют разработку функций (тесты должны быть изменены).

Большие тесты настолько сложны для написания, что даже сообщение в блоге Google выше утверждает, что очень немногие из них когда-либо должны быть написаны! Мне кажется, это противоречит здравому смыслу: конец конечные тесты проверяют вашу систему точно так же, как пользователь . Меньше проходов через систему почти всегда означает, что определенные ошибки будут проскальзывать и влиять на реальных пользователей.

С другой стороны, эффективно ли модульные тесты выявляют крайние случаи в производственной системе? Может быть. Возможно, нет. Я бы сказал, что пограничные случаи, которые видит реальная система, имеют большее значение. с обработкой ошибок в общей системе и как она реагирует на неверные данные, а не как действует конкретный небольшой фрагмент кода.

Это приводит к моему личному мнению, что пользователь выиграет от больше сквозных тестов и меньше модульных тестов (потому что они занимают время разработки).

Обычная тестовая пирамида имеет широкое основание и «заостренную» вершину. Что, если бы мы могли изменить форму пирамиды, чтобы лучше согласовать объем тестирования с целями пользователя?

Что мы можем сделать, чтобы изменить форму пирамиды?

Ну, мы сделали несколько вещей, чтобы изменить его.

1. Заменил некоторые модульные тесты на статические проверки типов, используя TypeScript. Там меньше нужно проверить, что происходит с a + b , когда a и b являются строками, если компилятор проверяет если аргументы всегда будут числами.
2. Настройте и используйте службы отчетов о сбоях, такие как Sentry / Raygun / и т. д. Мгновенный сбой отчетность в производственной среде приносит прямую пользу пользователям. Все ждут багов и сбоев, но многие пользователи в восторге, когда мы мгновенно узнаём о проблемах и разворачиваем патчи быстро.
3. Экспериментировал с партиями инструментов тестирования e2e для тестирования API и браузера. К счастью, есть новые интересные инструменты для тестирования браузеров, которые отдают предпочтение разработчикам. опыт, такой как Cypress, который позволяет нам писать тесты e2e так же просто, как модульные тесты .

С этими изменениями вот наша тестовая трапеция . и дешевые неизменяемые деплои, вместо которых мы можем просто пройти все тесты e2e.

Я буду рад обсудить наш подход к тестированию и философию, просто напишите мне по электронной почте или твит на @bahmutov

Соответствующие ссылки

• Руководство по сквозному тестированию от (неаффилированного) Guru99.
• Попытка TypeScript
• Неизменяемые развертывания с данными и тестированием
• Знай неизвестные неизвестные с Sentry
• Нирвана веб-тестирования с Cypress

Подписывайтесь на Глеба Бахмутова @bahmutov, посмотреть его проекты на glebbahmutov.com, посмотрите его видео о Cypress, просматривать его презентации

Хотите узнать больше о кипарисе? Проверьте кипарис. советы

Есть вопрос по кипарису? Хотите, чтобы я ответил на него? Поддержите меня через спонсоров GitHub или купив мои курсы Cypress.

Делиться Комментарии

• совет
• тестирование

2.5: Численное интегрирование — средняя точка, трапеция, правило Симпсона

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

10269

Эта страница является черновиком и находится в активной разработке.

Первообразные многих функций либо не могут быть выражены, либо не могут быть легко выражены в замкнутой форме (то есть через известные функции). b_af(x)\,dx\ ). Напомним, что сумма Римана функции \(f(x)\) по интервалу \([a,b]\) получается выбором разбиения 9n_{i=1}f(m_i)Δx\) соответствует сумме площадей прямоугольников, аппроксимирующих площадь между графиком \(f(x)\) и осью \(x\) над \([ а, б]\). На графике показаны прямоугольники, соответствующие \(M_4\) для неотрицательной функции на замкнутом интервале \([a,b].\)

Рисунок \(\PageIndex{1}\): Правило средней точки аппроксимирует площадь между график \(f(x)\) и оси \(x\) путем суммирования площадей прямоугольников со средними точками, являющимися точками на \(f(x)\).

Пример \(\PageIndex{1}\): использование правила средней точки с \(M_4\) 92\,dx\) с использованием четырех подынтервалов. Сравните результат с действительным значением этого интеграла.

Решение: Каждый подинтервал имеет длину \( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Следовательно, подынтервалы состоят из

\[\left[0,\ tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2} ,\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].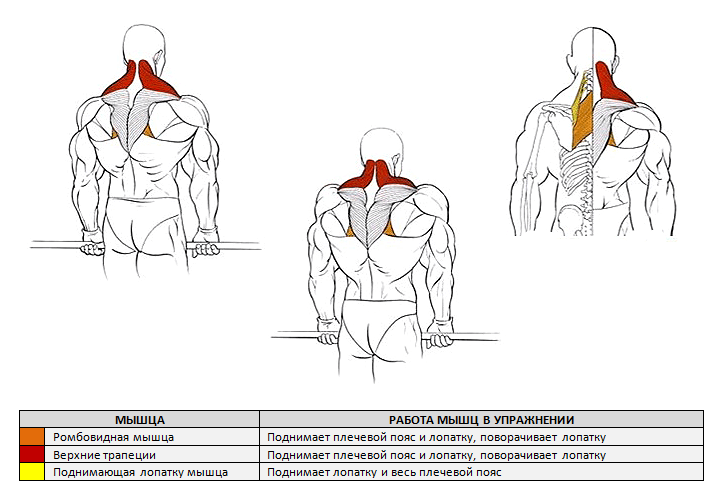 \nonumber\]

Середины этих подинтервалов являются \(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right \}.\) Таким образом, 92_1\frac{1}{x}\,dx.\)

Подсказка

\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)

Ответить

\(\dfrac{24}{35}\)

Правило трапеций

Мы также можем аппроксимировать значение определенного интеграла, используя трапеции, а не прямоугольники. На рисунке \(\PageIndex{2}\) область под кривой аппроксимирована трапециями, а не прямоугольниками.

Рисунок \(\PageIndex{2}\): Трапеции можно использовать для аппроксимации площади под кривой, таким образом, аппроксимируя определенный интеграл.

Правило трапеций для оценки определенных интегралов использует трапеции, а не прямоугольники для аппроксимации площади под кривой. Чтобы получить представление об окончательной форме правила, рассмотрите трапеции, показанные на рисунке \(\PageIndex{2}\). Мы предполагаем, что длина каждого подынтервала равна \(Δx\). Во-первых, напомним, что площадь трапеции с высотой \(h\) и длинами оснований \(b_1\) и \(b_2\) определяется выражением \(\text{Area}=\frac{1}{ 2}h(b_1+b_2)\). Мы видим, что первая трапеция имеет высоту \(Δx\) и параллельные основания длины \(f(x_0)\) и \(f(x_1)\). Таким образом, площадь первой трапеции на рисунке \(\PageIndex{2}\) равна 9b_af(x)\,dx≈\frac{Δx}{2}\big(f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f( x_4)\big).\nonumber\]

Обобщая, сформулируем формально следующее правило.

Правило трапеций

Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — натуральное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \( P=\{x_0,x_1,x_2…,x_n\}.\ )

Набор

\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_ {n−1})+f(x_n)\big).\] 9nf(x_i)Δx.\)

То есть \(L_n\) и \(R_n\) аппроксимируют интеграл, используя левую и правую конечные точки каждого подинтервала соответственно. Кроме того, внимательное изучение рисунка \(\PageIndex{3}\) позволяет нам сделать следующие замечания об использовании правил трапеций и правил середины для оценки определенного интеграла неотрицательной функции. Правило трапеций имеет тенденцию систематически завышать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически занижать значение определенного интеграла на интервалах, где функция вогнута вниз. С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично занижая значение определенного интеграла на тех же самых типах интервалов. Это приводит нас к гипотезе о том, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеций. 92_1\frac{1}{x}\,dx.\)

Подсказка

Набор \(Δx=\dfrac{1}{2}.\) Концы подынтервалов являются элементами множества \(P=\left\{1,\frac{3}{2},2\right \}.\)

Ответить

\(\dfrac{17}{24}\)

Абсолютная и относительная погрешность

Важным аспектом использования этих правил численной аппроксимации является вычисление погрешности их использования для оценки значения определенного интеграла. 2\,dx\), используя правило средней точки, найденное в Пример \(\PageIndex{1}\). 92_1\frac{1}{x}\,dx\) в \(\frac{24}{35}\) с использованием \(T_2\). Фактическое значение этого интеграла равно \(\ln 2\). Используя \(\frac{24}{35}≈0,6857\) и \(\ln 2≈0,6931,\), вычислите абсолютную ошибку и относительную ошибку.

Подсказка

Используйте предыдущие примеры в качестве руководства.

Ответить

абсолютная ошибка \(\приблизительно 0,0074,\) и относительная ошибка \(\приблизительно 1,1\%\)

Границы погрешности для средней точки и правил трапеций

В двух предыдущих примерах мы смогли сравнить нашу оценку интеграла с фактическим значением интеграла; однако у нас обычно нет такой роскоши. В общем, если мы аппроксимируем интеграл, мы делаем это потому, что не можем легко вычислить точное значение самого интеграла. Поэтому часто полезно иметь возможность определить верхнюю границу ошибки приближения интеграла. 2\,dx.\)

Подсказка

\(f»(x)=2,\) поэтому \(M=2.\)

Ответить

\(\dfrac{1}{192}\)

Правило Симпсона

С помощью правила средней точки мы оценили площади областей под кривыми с помощью прямоугольников. В некотором смысле мы аппроксимировали кривую кусочно-постоянными функциями. С помощью правила трапеций мы аппроксимировали кривую, используя кусочно-линейные функции. Что, если бы мы вместо этого аппроксимировали кривую с помощью кусочно-квадратичных функций? С 9{x_4}_{x_2}f(x)\,dx\) с интегралом от другой квадратичной функции, проходящей через \( (x_2,f(x_2)), \,(x_3,f(x_3)),\) и \((x_4,f(x_4)).\) Этот процесс продолжается с каждой последующей парой подынтервалов.

Рисунок \(\PageIndex{4}\): С помощью правила Симпсона мы приближаем определенный интеграл, интегрируя кусочно-квадратичную функцию.

Чтобы понять формулу, которую мы получаем для правила Симпсона, мы начнем с вывода формулы для этой аппроксимации для первых двух подынтервалов. Проходя через вывод, мы должны помнить о следующих соотношениях: 9{x_4}_{x_0}f(x)\,dx=\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f( x_3)+f(x_4)).\nonumber\]

Шаблон продолжается, когда мы добавляем пары подынтервалов к нашему приближению. Общее правило можно сформулировать следующим образом.

Правило Симпсона

Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — четное положительное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \(P=\{x_0,x_1,x_2,…,x_n\}. \) Набор 9b_af(x)\,dx.\nonumber\]

Точно так же, как правило трапеций является средним значением правил левой и правой руки для оценки определенных интегралов, правило Симпсона может быть получено из правил средней точки и правил трапеций с помощью взвешенное среднее. Можно показать, что \(S_{2n}=(\dfrac{2}{3})M_n+(\dfrac{1}{3})T_n\).

Также можно ограничить ошибку при использовании правила Симпсона для аппроксимации определенного интеграла. Граница ошибки задается следующим правилом: 92_1\frac{1}{x}\,dx.\)

Подсказка

\[S_2=(\frac{1}{3}Δx(f(x_0)+4f(x_1)+f(x_2))\]

Ответить

\(\фракция{25}{36}\)

---

Ключевые понятия

• Мы можем использовать численное интегрирование для оценки значений определенных интегралов, когда сложно найти замкнутую форму интеграла или когда требуется приблизительное значение только определенного интеграла.
• Наиболее часто используемыми методами численного интегрирования являются правило средней точки, правило трапеций и правило Симпсона.
• Правило средней точки аппроксимирует определенный интеграл, используя прямоугольные области, тогда как правило трапеций аппроксимирует определенный интеграл, используя трапециевидные приближения.
• Правило Симпсона аппроксимирует определенный интеграл, сначала аппроксимируя исходную функцию с помощью кусочно-квадратичных функций.