Золотое сечение — как его измерить? — ПолонСил.ру — социальная сеть здоровья
Принято считать, что понятие о золотом делении ввел Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. Высшую гармонию «золотого сечения» проповедовали и Леонардо да Винчи и Микеланджело… При этом ученые, вплоть до Эйнштейна, будут искать, но так и не найдут его точного числового значения. Бесконечный ряд после запятой — 1,6180339887…
Итак, что же такое золотое сечение?
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку.
Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная… Садясь на скамейку, вы произвели «золотое сечение».
Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная… Садясь на скамейку, вы произвели «золотое сечение».
Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение». Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение».
Все процессы, от микро до макро, которые происходят во вселенной имеют фрактальную структуру.
Фрактал — это самоподобная фигура, каждый фрагмент которой повторяется при уменьшении масштаба.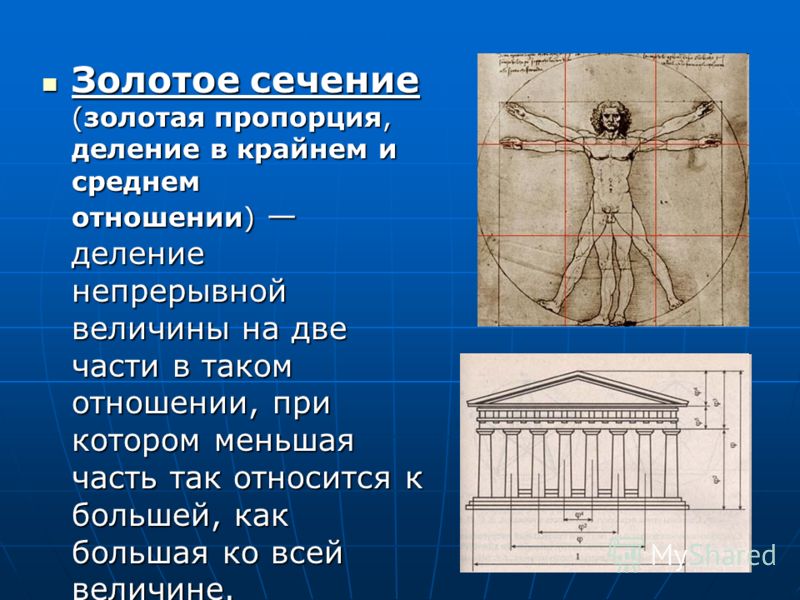
Золотой прямоугольник (то есть прямоугольник, стороны которых относятся в «золотом» соотношении)обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники.
В основе золотой спирали лежит золотое сечение — коэффициенты Фибоначчи
А золотая спираль лежит в основе всех процессов происходящих во вселенной, и даже спиральные галактики закручены по логарифмическим спиралям:
Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».
Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».
В конце 19 века немецкий профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он объявил в нем пропорцию золотого сечения универсальной для всех явлений природы и искусства.
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.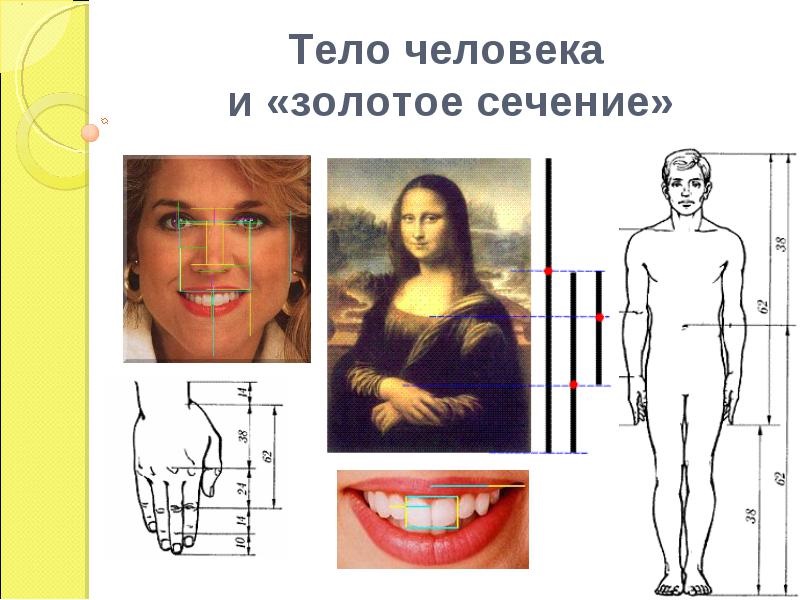
Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Cправедливость своей теории Цейзинг проверял на греческих статуях. Подверглись исследованию также греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому се
Золотое сечение: Как это работает?
Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.
Определение
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.
История
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой — Отца, а целое — Святой дух.
Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.
Природа
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.
Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
Человек
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек — это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.
В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела — 8:5.
Искусство пространственных форм
Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следовали этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.
Долгое время художники следовали этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.
Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.
Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.
Слово, звук и кинолента
Формы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34.
Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) — это и есть точка золотого сечения.
Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.
Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух — в Одессе. Переход на сцены в городе и есть золотая середина фильма.
Источник: Academic Painting
Золотое сечение. Божественная пропорция. Сакральная геометрия. Энергетические коды гармонии
Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое – деление отрезка в среднем и крайнем отношении.
И. Кеплер
Существуют вещи, которые практически невозможно объяснить. К примеру, вы подходите к пустой скамейке, и вам нужно на нее сесть. Где вы сядете? Возможно, прямо по центру. Возможно, с самого края. Но скорее всего, вы инстинктивно выберете такое положение, чтобы разделить скамейку на две части, относящиеся друг к другу в пропорции 1:1,62. Одним абсолютно простым действием вы разделили пространство по «золотому сечению».
Золотое сечение – деление величины (например, отрезка) на две части таким образом, при котором отношение большей части к меньшей равно отношению всей величины к ее большей части. Приблизительная величина золотого сечения равна 1,6.
Несмотря на почти мистическое происхождение, число PHI сыграло по-своему уникальную роль. Роль кирпичика в фундаменте построения всего живого на земле. Все растения, животные и даже человеческие существа наделены физическими пропорциями, приблизительно равными корню от соотношения числа PHI к 1. Эта вездесущность PHI в природе… указывает на связь всех живых существ. Раньше считали, что число PHI было предопределено Творцом Вселенной. Ученые древности называли одну целую шестьсот восемнадцать тысячных «божественной пропорцией».
Бесконечный ряд чисел:
Ученые веками пытались определить точное значение «золотой пропорции». Пифагор создал школу, где изучались тайны «золотого сечения», Евклид использовал его при создании геометрии, Аристотель применил к этическому закону, Леонардо да Винчи и Микеланджело будут воспевать его в своих работах. Что же это за божественная пропорция, силу и истинную суть которой не могут определить до сих пор? Золотое сечение можно увидеть везде: в бутонах цветов, в теле человека, в завитках ракушек. Что это – этический догмат? Мистическая тайна? Феномен? Или все вместе?
Пропорции золотого сечения, введенные в научный обиход еще Пифагором, используются и по сей день в искусстве, математике, повседневной жизни. К примеру, режиссер Сергей Эйзенштейн построил свой фильм «Броненосец Потемкин» по правилам золотого сечения. В первых трех частях действие происходит на корабле. В оставшихся двух – в Одессе. Момент перехода действия в Одессу точно совпадает с точкой золотого сечения.
Золотое сечение и зрительные центры
При изучении пирамид Хеопса выяснилось, что египетские мастера пользовались божественной пропорцией при создании самих пирамид, а также храмов, барельефов, украшений и предметов быта из гробницы Тутанхамона.
В фасаде одного из семи чудес света, Парфенона, также присутствуют золотые пропорции. При раскопках этого храма были найдены циркули, которыми пользовались зодчие античного мира.
Секреты золотого сечения в античности были доступны только посвященным. Их тайна ревностно охранялась и разглашалась только в особых случаях.
В эпоху Возрождения интерес к золотому сечению усиливается, особенно в искусстве и архитектуре. Особенное внимание к божественной пропорции питал великий ученый и художник Леонардо да Винчи. Он даже было начал писать книгу по геометрии, но его опередил монах Лука Пачоли, который и дал новое название золотому сечению – «божественная пропорция». В его книге, которая так и называлась, «Божественная пропорция», говорилось о том, что маленький отрезок величины золотого сечения – это олицетворение Бога-Сына. Большой отрезок – это Бог-Отец, а вся величина целиком – это единство, это Бог Духа Святого. Божественная суть божественной пропорции…
Схема Парфенона
Изучение пропорций человеческого тела
Леонардо да Винчи, в свою очередь, ввел в обиход название «золотое сечение». Он много внимания уделял в своих исследованиях золотому делению. Не раз производя сечение стереометрического тела пятиугольниками, он получал прямоугольники с соотношениями сторон в золотом делении. Отсюда и пошло самое популярное название классической пропорции – золотое сечение.
Золотое сечение
Золотое сечение
Бабенко П.Д. 11КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ И.Т. ТРУБИЛИНА
Мамась Н.Н. 11КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ И.Т. ТРУБИЛИНА
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение: «Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением…»
«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».
Иоганн Кеплер
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Цели:
1. Измерить гармонию алгеброй.
2. Изучить разнообразие применения золотого сечения и связанные с ним соотношения в реальной жизни;
2. Разобраться в пропорциях человека как гармонии и красоты.
Задачи:
1. Познакомиться с понятием золотого сечения и с историей его развития;
2. Получить представление о практическом применении золотого сечения в реальной жизни;
3. Выяснить, почему с этим понятием связана гармония и красота.
Предметом исследования является золотое сечение, объектом – гармоническая пропорция.
Актуальность работы – гармония и красота в жизни всегда актуальны
Гипотеза: в окружающем мире “золотое сечение” является основополагающим принципом красоты, прочности, надежности и позволяет осознать связь мира искусства и мира чисел.
1. Понятие «золотое сечение».
«Золотым сечением» и даже «божественной пропорцией» называли математики древности и средневековья такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
а :b = b : c или с : b = b : а
Итак, золотая пропорция = 1 :1,618. Это отношение приближенно равно 0,618 ≈ 5/8.В алгебре это число обозначается греческой буквой фи (φ). Полученное значение есть знаменитое число «фи», названное так американским математиком Марком Баром по первой букве имени великого скульптора Фидия, который, по преданию, использовал «золотое сечение» в своих работах.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник — выпуклый и звездчатый.
Из подобия треугольников АСD и ABE можем вывести уже известную пропорцию:
AB/AC=AC/BC
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.1.1. Задачи на построение.
В геометрии есть понятия: «деление отрезка в золотом отношении», «золотой треугольник», «золотой прямоугольник», «золотая логарифмическая спираль». Мне Dзахотелось научиться строить эти фигуры. Я разобрала три задачи.
Задача №1. «Деление отрезка в золотом отношении»
Дано : Отрезок АВ. E
A CB Построить: золотое сечение отрезка АВ, то есть точку С так, чтобы Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.
Задача №2. Построение «золотого треугольника».
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции «золотого сечения». Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника
2. История развития «золотого сечения».
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор.
Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети 1 в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответсвуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.Также о золотом делении знал Платон. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во второй книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипеикл (2 в. до н.э.), Папп (3 в. н.э.) и др.
В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж.Кампано из Наварры (3 в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре. В 1509 г. В Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства Бог сын, Бог отец и Бог дух святой (подразумевалась, что малый отрезок есть олицетворение Бога сына, большой отрезок – Бога отца, а весь отрезок – Бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название Золотое Сечение. Так оно и держится до сих пор как самое популярное.
В 1855 г. Немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.
В конце 19 – начале 20 вв. появилось немало чисто формалистических теорий о применении золотого сечения в произведениях искусства и архитектуры.
3. «Золотое сечение» в разных сферах
3.1.«Золотое сечение» в скульптуре.
Скульптурное сооружение, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния. Ещё в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Они утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения».
Великий древнегреческий скульптор Фидий часто использовал «золотое сечение» в своих произведениях. Самая знаменитая статуя Зевса Олимпийского и Афины Парфенос (которые считались одним из чудес света). Было проведено большое число измерений на помещённых в журналах крупных портретах мужчин и женщин, на многих их низ указанные отношения представляют «золотое сечение».
3.2.«Золотое сечение» в архитектуре.
Парфенон.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (5 в. До н. э.).
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон(синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.
Дом Пашкова.
Одним из шедевров архитектуры в Москве – дом Пашкова- является одним из наиболее совершенных произведений архитектуры В. Баженова. Прекрасное творение вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.
Баженов говорил: «Архитектура – главнейшее имеет три предмета; красоту, спокойность и прочность здания… К достижению сего служит руководством здание пропорций, перспектива, механика или вообще физика, а всем им общим является рассудок».
3.3. «Золотое сечение» в живописи.
«Золотое сечение» в живописи, проглядывалось в работах и творчесте великого Леонардо да Винчи. Он говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Одним из таких портретов является Монны Лизы (Джоконды), долгие годы привлекают внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует много версий об истории этого портрета. Одна из них:
Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекало простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.
3.4. «Золотое сечение» в природе.
«Золотое сечение» — один из основополагающих принципов природы. Красота природных форм во взаимодействии двух физических сил – тяготения и инерции. Золотое сечение – символ этого взаимодействия, поскольку диктуемое ею отношение большей части целого к самому целому выражает основные моменты живого роста: стремительный рост побега до зрелости и замедленный рост до момента цветения, когда достигшее полной силы растение готовится дать жизнь новому побегу.
Одним из первых проявления золотого сечения в природе подметил немецкий математик и астроном Иоганн Кеплер (1570-1630 гг.). С ХVII в. наблюдение математических закономерностей в ботанике и зоологии стали быстро накапливаться.
В 1850 г. немецкий ученый А. Цейзинг открыл так называемый закон углов, согласно которому средняя величина углового отклонения ветки растения равно примерно 138 градусов.
Допустим, что две соседние ветки растения исходят из одной точки (на самом деле это не так: в реальности ветви располагаются выше или ниже друг друга). Обозначим одну из них через ОА, другую через ОВ. Угол между лучами – ветками обозначим через а, а угол, дополняющий его до 360 , — через Р.
Составим золотую пропорцию деления полного угла, считая, что угол К – большая часть этой величины.
360/Р=Р/360-Р.
Получаем квадратное уравнение: Р² + 360 – Р360² =0. Положительный корень Р= -180+√180²+360²= 180·±√5= 180·1,236= 222,48.
а=360°-222,48°=137,52°≈138°.
Таким образом, величина среднего углового отклонения ветки соответствует меньшей из двух частей, на которые делится полный угол при золотом сечении.
5. Экспериментальная часть
Изучив теорию вопроса, я решила провести исследование и найти пропорции золотого сечения в живой природе (на примере комнатных растений).
Эксперимент №1
Цель: проверить есть ли «золотое сечение» в растительном мире, у комнатных растений.
В первую очередь я заинтересовалась, как проявляется принцип формообразования в живой природе. Выяснилось, что комнатные растения растут и занимают место в пространстве в основном в двух вариантах — рост вверх или расстилание по поверхности, либо закручивание по спирали (вьющиеся растения). Меня заинтересовал первый вариант. Для этого было изучено 6 комнатных растений (среди них бегония клубневая, диффенбахия, традесканция, глоксиния белоцветковая, каланхое, роициссус).
Приглядимся внимательно к схематично изображённому фрагменту комнатного растения. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.
Если измерить расстояние АС и расстояние ВС, и найти отношение
ВС.: АС, то оно приближённо равно 0,618, т.е. подчиняется золотой пропорции.
Вывод: результаты измерений показывают, что в росте, завоевании пространства, растение сохраняет определенные пропорции. Импульсы его роста постепенно уменьшаются в пропорции «золотого сечения».
Заключение.
В своей работе я хотел продемонстрировать красоту и широту «Золотого сечения» в реальной жизни. Проведенные исследования доказали, что многое в окружающем мире подчиняется правилу золотого сечения.
Физика исследует реальный мир. Биология – живой мир органической природы. Предмет исследования математики нематериальны, в природе нет логарифмов, синус не рассмотришь под микроскопом и при этом математика – самое могущественное орудие познания, созданное человеком, и любая наука достигает совершенства, когда начинает говорить на языке математики.
Значение золотого сечения в современной науке очень велико. Эта пропорция используется практически во всех областях знаний.
Я говорила только об его эстетическом значении, но существуют примеры его чисто практического применения. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью и т.д.
Список литературы:
Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014.
Пидоу Д. Геометрия и искусство. – М.: Мир, 1989.
Виленкин Н. и др. «Математика», 5, «Мнемозина», 2001
«Энциклопедический словарь юного математика», Москва, «Педагогика», 1985
Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988.
Интернет сайты:
http://www.abc-people.com/idea/zolotsech/
http://n-t.ru/tp/iz/zs.htm
http://tmn.fio.ru/works/04x/304/p3_4.htm
Просмотров работы: 661
Что такое золотое сечение простыми словами. Что нужно знать о золотом сечении.
Что такое золотое сечение простыми словами. Что нужно знать о золотом сечении.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина — 1, 6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение в формах пространства и времени действует.
История.
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах лука пачоли в книге «Божественная Пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял сына, большой — отца, а целое — святой дух. Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. на отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два Младших Члена Этой Нескончаемой Пропорции в Сумме Дают Третий Член, а Любые два Последних Члена, Если их Сложить, Дают Следующий Член, Причем та же Пропорция Сохраняется до Бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях. Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении. Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «Математическое Эстетство» вызывало много критики.
Природа.
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть. Белорусский ученый Эдуард сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали. Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «Кривой Жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение днк и даже структура галактик заключают в себе ряд Фибоначчи.
Человек.
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек — это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды. В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле корбюзье, используя «Витрувианского Человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века. Адольф цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа. В результате измерений исследователь установил, что пропорции мужского тела 13: 8 ближе к золотому сечению, чем пропорции женского тела — 8: 5.
Искусство пространственных форм.
Художник Василий суриков говорил, «что в Композиции Есть Непреложный Закон, Когда в Картине Нельзя Ничего ни Убрать, ни Добавить, Даже Лишнюю Точку Поставить Нельзя, это Настоящая Математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль. Искусствовед Ф. в. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в Селе Михайловском», отмечает, что каждая деталь полотна будь — то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции. Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке великие пирамиды гизы, собор парижской богоматери, храм Василия блаженного, Парфенон. И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение. Слово, звук и кинолента формы временно? Го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34. Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой Дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853: 535=1, 6) — это и есть точка золотого сечения. Советский музыковед э. к. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение. Кинорежиссер Сергей эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух — в Одессе. Переход на сцены в городе и есть золотая середина фильма. (С) Дмитрий богачь.
Золотое сечение, что это такое простыми словами. Что такое золотое сечение?
Что общего у египетских пирамид, картины «Мона Лиза» Леонардо да Винчи и логотипов Twitter и Pepsi?
Не будем тянуть с ответом – все они созданы с использованием правила золотого сечения. Золотое сечение – это соотношение двух величин а и b, которые не равны между собой. Данная пропорция часто встречается в природе, также правило золотого сечения активно используется в изобразительном искусстве и дизайне – композиции, созданные с использованием «божественной пропорции», хорошо сбалансированы и, что называется, приятны для глаз. Но что именно представляет собой золотое сечение и можно ли использовать его в современных дисциплинах, к примеру, в веб-дизайне? Давайте разберемся.
НЕМНОГО МАТЕМАТИКИ
Допустим, у нас есть некий отрезок АБ, разделенный надвое точкой С. Соотношение длин отрезков: AC/BC = BC/AB. То есть, отрезок разделен на неравные части таким образом, что большая часть отрезка составляет такую же долю в целом, неразделенном отрезке, какую меньший отрезок составляет в большем.
Такое неравное разделение и называется золотым сечением. Обозначается золотое сечение символом φ. Значение φ составляет 1,618 или 1,62. В общем, если говорить совсем просто, это деление отрезка или любой другой величины в отношении 62% и 38%.
«Божественная пропорция» была известна людям с древнейших времен, этим правилом пользовались при возведении египетских пирамид и Парфенона, золотое сечение можно обнаружить в росписи Сикстинской капеллы и на картинах Ван Гога. Широко используется золотое сечение и в наши дни – примеры, которые постоянно у нас перед глазами – это логотипы Twitter и Pepsi.
Человеческий мозг устроен таким образом, что он считает красивыми те изображения или объекты, в которых можно обнаружить неравное соотношение частей. Когда мы говорим о ком-то, что «он пропорционально сложен», мы, сами того не ведая, имеем в виду золотое сечение.
Золотое сечение можно применять к различным геометрическим фигурам. Если взять квадрат и умножить одну его сторону на 1,618, то мы получим прямоугольник.
Теперь, если наложить квадрат на этот прямоугольник, мы сможем увидеть линию золотого сечения:
Если продолжать использовать эту пропорцию и разбивать прямоугольник на более мелкие части, мы получим вот такую картину:
Пока еще не понятно, куда нас заведет это дробление геометрических фигур. Еще чуть-чуть и все станет ясно. Если в каждом из квадратов схемы провести плавную линию, равную четвертинке окружности, то мы получим Золотую спираль.
Это необычная спираль. Ее еще иногда называют спиралью Фибоначчи, в честь ученого, который исследовал последовательность, в которой каждое число рано сумме двух предыдущих. Суть в том, что это математическое соотношение, визуально воспринимаемое нами как спираль, встречается буквально повсюду – подсолнухи, морские раковины, спиральные галактики и тайфуны – везде есть золотая спираль.
КАК МОЖНО ИСПОЛЬЗОВАТЬ ЗОЛОТОЕ СЕЧЕНИЕ В ДИЗАЙНЕ?
Итак, теоретическая часть окончена, переходим к практике. Неужели золотое сечение можно использовать в дизайне? Да, можно. К примеру, в веб-дизайне. Учитывая данное правило, можно получить правильное соотношение композиционных элементов макета. В результате все части дизайна, вплоть до самых маленьких, будут гармонично сочетаться между собой.
Если взять типичный макет с шириной 960 пикселей и применить к нему правило золотого сечения, то мы получим вот такую картину. Соотношение между частями составляет уже известное 1:1,618. В результате мы имеем двухколоночный макет, с гармоничным сочетанием двух элементов.
Сайты с двумя колонками встречаются очень часто и это далеко не случайно. Вот, к примеру, сайт National Geographic. Две колонки, правило золотого сечения. Хороший дизайн, упорядоченный, сбалансированный и учитывающий требования визуальной иерархии.
Еще один пример. Дизайн-студия Moodley разработала фирменный стиль для фестиваля исполнительского искусства в Брегенце. Когда дизайнеры работали над афишей мероприятия, они однозначно пользовались правилом золотого сечения для того, чтобы верно определить размер и расположения всех элементов и в результате получить идеальную композицию.
Агентство Lemon Graphic, создавшее визуальный образ для компании Terkaya Wealth Management, также использовала соотношение 1:1,618 и золотую спираль. Три элемента дизайна визитной карточки прекрасно вписываются в схему, в результате чего все части очень хорошо сочетаются между собой
А вот еще интересное использование золотой спирали. Перед нами опять сайт National Geographic. Если взглянуть на дизайн повнимательнее, то можно увидеть, что на странице есть еще один логотип NG, только поменьше, который расположен ближе к центру спирали.
Разумеется, это не случайно – дизайнеры прекрасно знали, что они делают. Это отличное место, чтобы продублировать логотип, так как наш глаз, рассматривая сайт, естественным образом смещается к центру композиции. Так работает подсознание и это необходимо учитывать при работе над дизайном.
ЗОЛОТЫЕ КРУГИ
«Божественная пропорция» может применяться к любым геометрическим фигурам, в том числе и к кругам. Если вписать окружность в квадраты, соотношение между которыми составляет 1:1,618, то мы получим золотые круги.
Вот логотип Pepsi. Все ясно без слов. И соотношение, и то, как была получена плавная дуга белого элемента логотипа.
С логотипом Twitter все немного сложнее, но и здесь видно, что его дизайн основан на использовании золотых кругов. Он немного не соответствует правилу «божественной пропорции», но по большей части все его элементы вписываются в схему.
ВЫВОД
Как видно, несмотря на то, что правило золотого сечения известно с незапамятных времен, оно нисколько не устарело. Следовательно, его можно использовать в дизайне. Не обязательно изо всех сил стараться уложиться в схему – дизайн дисциплина неточная. Но если нужно добиться гармоничного сочетания элементов, то попробовать применить принципы золотого сечения не помешает.
Что такое золотое сечение где оно встречается и для чего применяется. Золотое сечение в природе и искусстве
Человечество за всю историю открыло несколько уникальных закономерностей, которые нашли широкое применение в самых разнообразных областях. Одна из них – золотое сечение.
Оно описывает разделение объекта на 2 части в том соотношении, в котором меньшая часть относится к большей, так же как большая часть относится к полному размеру объекта. В качестве примера этого запутанного определения можно привести деление прямоугольного листа: отрезая от полного листочка меньший прямоугольник, у последнего окажется то же соотношение сторон, что и у большого. Еще один пример – звезда с пятью концами: в этой геометрической фигуре каждый отрезок, соединяющий её лучи, разделяется по данному правилу пересекающим его отрезком.
Как появилось правило золотого сечения?
История возникновения уходит в далекое прошлое. Его описывал в труде «Начала» древний ученый и мыслитель Евклид, это первые документальные упоминания. Древнегреческий математик не единственный, кто заметил и активно использовал правило. Значительно позже его применял и Леонардо да Винчи, называя «божественной пропорцией», и Мартин Ом. Последний в 1835 году ввел в обиход этот термин.
Где можно встретить?
Золотое сечение в природе можно заметить у растений: они при росте сохраняют заданные пропорции. А немецкий ученый Цейзинг установил, что деление человеческого тела в точке пупка также соответствует данному правилу. Отмечено явление и в следующих областях:
- архитектура – египетские пирамиды, построенные много веков назад;
- музыка – произве
Золотое сечение — Википедия. Что такое Золотое сечение
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число
- Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Иллюстрация к определениюЧисло Φ{\displaystyle \Phi } называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16]
Математические свойства
Калькулятор соотношенияИспользование калькулятора
Калькулятор соотношений выполняет три типа операций и показывает шаги для решения:
- Упростите отношения или создайте эквивалентное соотношение, когда одна сторона отношения пуста.
- Решите отношения для одного отсутствующего значения при сравнении соотношений или пропорций.
- Сравните отношения и оцените их как истинное или ложное, чтобы ответить, эквивалентны ли отношения или дроби.
Этот калькулятор соотношений принимает целые числа, десятичные дроби и научную электронную запись с ограничением до 15 символов.
Коэффициенты упрощения:
Введите A и B, чтобы найти C и D. (или введите C и D, чтобы найти A и B)
Калькулятор упростит соотношение A: B, если это возможно.В противном случае калькулятор найдет эквивалентное соотношение, умножив каждый из A и B на 2, чтобы получить значения для C и D.
Сравните коэффициенты и найдите недостающее значение:
Введите A, B и C, чтобы найти D.
Калькулятор показывает шаги и решает для D = C * (B / A)
Введите A, B и D, чтобы найти C.
Калькулятор показывает шаги и решает для C = D * (A / B)
Оценить эквивалентные соотношения:
Введите A, B, C и D.
Эквивалентно ли соотношение A: B соотношению C: D? Калькулятор находит значения A / B и C / D и сравнивает результаты, чтобы оценить, является ли утверждение истинным или ложным.
Преобразование Соотношение в Дробь
Частичное соотношение определяет соотношение частей по отношению друг к другу. Сумма частей составляет целое. Соотношение 1: 2 читается как «1 к 2». Это означает, что из трех целых одна часть стоит 1, а другая — 2.
Чтобы преобразовать частичное соотношение в дроби:
- Добавьте коэффициенты отношения, чтобы получить целое. Используйте это как знаменатель.
1: 2 => 1 + 2 = 3 - Преобразуйте соотношение в дроби. Каждый член отношения превращается в числитель в дроби.
1: 2 => 1/3, 2/3 - Следовательно, при соотношении частей к частям 1: 2, 1 составляет 1/3 целого, а 2 — 2/3 целого.
Сопутствующие калькуляторы
Чтобы уменьшить коэффициент до наименьшего целого числа, см. Ratio Simplifier.
Чтобы преобразовать дробь в сокращенную или смешанное число, используйте нашу Упрощающий калькулятор дробей.
Золотое сечение Акшата Раджана.Что такое золотое сечение? Золотое сечение — это иррациональное число. Если человек попытается это написать, он никогда не остановится.
Презентация на тему: «Золотое сечение Акшата Раджана. Что такое золотое сечение? Золотое сечение — это иррациональное число. Если человек попытается написать его, он никогда не остановится» — стенограмма презентации:
1 Золотое сечение Акшата Раджана
2 Что такое золотое сечение? Золотое сечение — это иррациональное число.Если человек попытается написать его, он никогда не остановится и никогда не будет прежним снова и снова, но это начнется так — 1,6180339887 … (приблизительно). Важная особенность этого числа в том, что человек может вычесть из него 1 или разделите на него 1. В любом случае он найдет тот же номер. Математика имеет отношение ко всему. Из этой презентации вы узнаете, как это связано с красотой. Вы можете назвать кого-нибудь красивым, используя математику. Золотое сечение 1: 1,6.
3 MY FACE Ширина перемычки = 15 мм Ширина глаза = 14 мм Отношение перемычки / глаза = 15:14 Ширина рта = 18 мм Ширина зуба = 16 мм Отношение рот / зубы = 9: 8 Эти 2 соотношения не одинаковы, но немного близки.
4 Сравнение лиц (9 одноклассников) Имя: Ширина переносицы (мм) Ширина глаз (мм) Соотношение переносицы и глаза Ширина рта (мм) Ширина зубов (мм) Соотношение M / T Адитья 0,3 0,3: 0,30,90,50,9: 0,5 Arnav 35307: 875605: 4 Акшат 30365: 640258: 5 Джахнави 35257: 560506: 5 Каэваан Акаш 40 1: 1704514: 9 Ратиша 423742: 37794979: 49 Нишна 60403: 290603: 2 Сиддхант 35 1: 175605: 4
5 Общее соотношение B / E одноклассников = 66: 60 Среднее = 11:30 Общее соотношение M / T = 120: 78 Среднее = 20: 13 Эти соотношения в основном были разными, но некоторые были похожи.Они немного отличались. Среднее значение 20:13. В одном — Нишна, остальные похожи, но не все.
6 Ширина мостика для взрослых Face My Mom = 15 мм Ширина глаз = 14 мм Соотношение мостика / глаз = 15:14 Ширина рта = 18 мм Ширина зубов = 16 мм Соотношение рот / зубы = 9: 8
7 3 знаменитости Имя: BridgeEyeB / E Соотношение MouthTeethM / T Diana Argon 30503: 580608: 6 Дипика Пудоконе 222011: 10322016: 13 Бипаша Басу 70807: 812106: 5
8 Результат не так уж и отличается.Мои мамы и актрисы недалеко друг от друга! Так может потому, что моя мама красивая.
10 В ЭТОМ ШТАММЕ этот штамп пропорционален! Он точно выполнен по золотому сечению!
11 Это подсолнух золотого сечения! Когда это простая дробь. Узор из семян — спираль.
12 И много картин! Ее лицо — точно золотой прямоугольник !! отношение ширины ее лба к длине от макушки до подбородка.Так что математика используется даже при рисовании! (Междисциплинарный)
примеров золотого сечения, которые можно найти в природе
Часто говорят, что математика содержит ответы на большинство вопросов вселенной. Математика проявляется везде. Одним из таких примеров является золотое сечение. Эта знаменитая последовательность Фибоначчи очаровывала математиков, ученых и художников на протяжении многих сотен лет. Золотое сечение проявляется во многих местах Вселенной, в том числе прямо здесь, на Земле, оно является частью природы Земли и частью нас.
Мы уже говорили о рядах Фибоначчи и золотом сечении, но стоит сделать небольшой обзор. В математике последовательность Фибоначчи — это порядок чисел в следующей целочисленной последовательности: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… и так далее до бесконечности. Каждое число представляет собой сумму двух предшествующих ему чисел.
Последовательность Фибоначчи видна повсюду вокруг нас. Давайте посмотрим, как ваше тело и различные предметы, например морские ракушки и цветы, демонстрируют последовательность действий в реальном мире.
Как вы, наверное, уже знаете, последовательность Фибоначчи проявляется в самых неожиданных местах. Вот некоторые из них:
1. Лепестки цветов
Число лепестковв цветке часто является одним из следующих чисел: 3, 5, 8, 13, 21, 34 или 55. Например, у лилии три лепестка, у лютиков их пять, у цикория их 21. , ромашка часто имеет 34 или 55 лепестков и т. д.
2. Лица
Лица, как человеческие, так и нечеловеческие, изобилуют примерами золотого сечения.Рот и нос расположены на золотых сечениях расстояния между глазами и нижней частью подбородка. Подобные пропорции просматриваются сбоку, да и сам глаз и ухо.
3. Кузовные детали
Золотое сечение проявляется в строении человеческого тела. Человеческое тело основано на Фи и цифре 5. Придатки числа 5 к туловищу, в руках, ногах и голове. По 5 придатков на каждом из них, на пальцах рук и ног, и по 5 отверстий на лице.
Тела животных демонстрируют похожие тенденции.
4. Высевающие головки
Обычно семена производятся в центре, а затем перемещаются наружу, заполняя все пространство. Подсолнухи — отличный пример этих спиральных узоров.
5. Фрукты, овощи и деревья
Спиральные узоры можно найти на ананасах и цветной капусте. Числа Фибоначчи проявляются в разветвлении деревьев или количестве листьев на стебле цветка; числа вроде 4 — нет.Комбинации 3 и 5 встречаются в природе в изобилии.
6. Корпуса
Раковины улиток и наутилусов следуют по логарифмической спирали, как и улитка внутреннего уха. Его также можно увидеть в рогах некоторых коз и в форме паутины некоторых пауков.
7. Спиральные галактики
Спиральные галактики — самая распространенная форма галактик. У Млечного Пути есть несколько спиральных рукавов, каждое из которых представляет собой логарифмическую спираль около 12 градусов.
8. Ураганы
Удивительно, насколько мощные вихри урагана соответствуют последовательности Фибоначчи.
9. Молекулы ДНК
Молекула ДНК имеет размеры 34 ангстрем в длину и 21 ангстрем в ширину для каждого полного цикла двойной спирали. Эти числа 34 и 21 являются числами в ряду Фибоначчи, и их отношение 1,6190476 близко приближается к Фи, 1,6180339.
Прокрутите вниз и посмотрите фото примеров золотого сечения в природе.
Фото галерея
Калькулятор теоремы Байеса— вычисляет вероятность события с применением правила Байеса
Воспользуйтесь онлайн-калькулятором теоремы Байеса , чтобы получить вероятность события A, обусловленного другим событием B, с учетом априорной вероятности A и вероятностей B условной на A и B при условии ¬A.При решении обратной задачи инструмент применяет теорему Байеса (формула Байеса, правило Байеса) для определения апостериорной вероятности после наблюдения B.
Теорема Байеса (формула Байеса, правило Байеса)
Теорема Байеса названа в честь преподобного Томаса Байеса (1701–1761), в рукописи которого отражено его решение обратной вероятностной задачи: вычисление апостериорной условной вероятности события при известных априорных вероятностях, связанных с событием и соответствующими условиями.Он был опубликован посмертно при значительном вкладе Р. Прайса [1] , а затем переоткрыт и расширен Пьером-Симоном Лапласом в 1774 году.
В нынешнем виде теорема Байеса обычно выражается этими двумя уравнениями:
, где A и B — события, P () означает «вероятность» и | означает «при условии» или «дано». В этом калькуляторе Байеса используются обе формы теоремы Байеса.
Первую формулировку правила Байеса можно прочитать так: вероятность события A для данного события B равна вероятности события B для данного A, умноженной на вероятность события A, деленную на вероятность события B. В статистике P ( B | A) — это вероятность B при A, P (A) — это априорная вероятность A, а P (B) — предельная вероятность B. Альтернативная формулировка (2) выводится из (1) в развернутой форме P (B), в котором A и ¬A (not-A) являются несвязанными (взаимоисключающими) событиями.Эта формулировка полезна, когда мы не знаем напрямую безусловную вероятность P (B).
Формула Байеса имеет множество применений в теории принятия решений, обеспечении качества, фильтрации спама и т. Д. Этот калькулятор теорем Байеса позволяет вам исследовать ее значение в любой области. С распределением вероятностей подключено вместо фиксированных вероятностей она является краеугольным камнем в весьма спорной области байесовского вывода (статистика байесовской).
Практическое применение теоремы Байеса
Здесь мы представляем несколько практических примеров использования правила Байеса для принятия решения, а также некоторые общие ошибки и ограничения, которые следует соблюдать при применении теоремы Байеса в целом.
Диагноз рака
Женщина приходит на плановое обследование на рак груди с использованием маммографии (радиологического обследования). В среднем скрининг маммографа имеет ожидаемую чувствительность около 92% и ожидаемую специфичность 94%. Чувствительность отражает процент правильно идентифицированных раковых образований, а специфичность отражает процент правильно идентифицированных здоровых людей. Их дополнения отражают количество ложноотрицательных и ложноположительных результатов соответственно. Мы также знаем, что заболеваемость раком груди среди всего женского населения составляет 0.089%.
Подставив числа в наш калькулятор по теореме Байеса, мы увидим, что вероятность того, что женщина произвела тестирование и даст положительный результат на рак, составляет всего 1,35%. Довольно нелогично, правда?
Однако приведенный выше расчет предполагает, что мы больше ничего не знаем о женщине или процедуре тестирования. Тогда давайте сузим круг вопросов. Если мы также знаем, что женщине 60 лет и что уровень распространенности для этой демографической группы составляет 0,351% [2] , это приведет к новой оценке 5.12% (в 3,8 раза выше) для вероятности того, что у пациента действительно рак, если тест положительный.
Теперь, если мы также знаем, что тест проводится в США, и считаем, что чувствительность тестов, выполненных в США, составляет 91,8%, а специфичность — всего 83,2% [3] , мы можем пересчитать эти более точные числа, и мы увидим что вероятность того, что у женщины действительно будет рак при положительном результате, увеличена до 16,58% (в 12,3 раза больше по сравнению с исходным), в то время как вероятность того, что у нее будет рак при отрицательном результате, увеличена до 0.6613% (114 раз! Против исходного).
В этом примере вы можете увидеть как преимущества , так и недостатки и ограничения применения правила Байеса . Во-первых, очевидно, что чувствительность теста сама по себе является плохим предиктором вероятности того, что у женщины будет рак груди, что вполне естественно, поскольку это число ничего не говорит нам о частоте ложных срабатываний, что является важным фактором. когда базовая ставка низкая. Мы также должны принять во внимание специфичность, но даже при 99% -ной специфичности вероятность того, что у нее действительно будет рак после положительного результата, чуть ниже 1/4 (24.48%), что намного лучше, чем чувствительность 83,2%, которую наивный человек приписал бы своей вероятности. Сопоставление результатов теста с соответствующей исходной информацией полезно для определения фактической вероятности.
Однако также может ввести в заблуждение, если мы не используем правильную базовую скорость или коэффициенты специфичности и чувствительности , например, если мы применяем базовую ставку, которая носит слишком общий характер и не отражает всю информацию, которую мы знаем о женщине, или если измерения ошибочны / крайне недостоверны.Это известно как проблема эталонного класса и может быть серьезным препятствием в практическом использовании результатов калькулятора формулы Байеса.
Например, если истинная заболеваемость раком для группы женщин с ее характеристиками составляет 15% вместо 0,351%, вероятность того, что она действительно болеет раком после положительного результата скрининга, рассчитывается по теореме Байеса и составляет 46,37%, что составляет В 3 раза выше, чем наивысшая оценка, в то время как ее шанс заболеть раком после отрицательного результата скрининга составляет 3.48%, что в 5 раз выше самой высокой оценки. Вот почему опасно применять формулу Байеса в ситуациях, когда существует значительная неопределенность в отношении задействованных вероятностей или когда они не полностью охватывают известные данные, например потому что данные на уровне населения недоступны.
Тест на наркотики
Допустим, тест на наркотики с точностью 99,5% правильно определяет, употреблялся ли наркотик в течение последних 6 часов. Это также дает отрицательный результат у 99% протестированных непользователей.Учитывая, что использование этого препарата среди населения в целом составляет всего 2%, если у человека положительный результат теста на препарат, какова вероятность того, что он действительно получит наркотики? Используя этот калькулятор правила Байеса, вы можете увидеть, что вероятность составляет чуть более 67%, что намного меньше, чем можно было бы предположить по показаниям точности инструмента.
Конечно, как и в приведенном выше примере, этот расчет выполняется только в том случае, если мы больше ничего не знаем о тестируемом человеке. Однако, если мы знаем, что он принадлежит к группе высокого риска (распространенность 30%), а также демонстрирует неустойчивое поведение, тогда апостериорная вероятность равна 97.71% или выше: гораздо ближе к наивно ожидаемой точности. Однако, если мы также знаем, что среди таких демографических данных тест имеет более низкую специфичность — 80% (т.е. из-за того, что он активизируется при использовании, которое произошло за 12 или 24 часов до теста), тогда калькулятор выдаст вероятность только 68,07%, что еще раз демонстрирует что результат вычисления формулы Байеса может быть очень чувствительным к точности введенных вероятностей.
Гарантия качества
Теорема Байеса может быть полезна в сценарии обеспечения качества.Если у нас есть 4 машины на заводе, и мы заметили, что машина A очень надежна с уровнем продукции ниже порога QA, равным 1%, машина B менее надежна с показателем 2%, машина C имеет процент брака продукции 4% и, наконец, машина D: 5%. Если мы знаем, что A производит 35% всех продуктов, B: 30%, C: 15% и D: 20%, какова вероятность того, что данный дефектный продукт поступил из машины A?
В этом случае общее преобладание продуктов из машины А составляет 0,35. P (неудачный QA | произведенный машиной A) составляет 1%, а P (неудачный QA | ¬ произведенный машиной A) — это сумма интенсивностей отказов других 3 машин, умноженная на их долю в общем выпуске, или P (неудачный QA | ¬ производится машиной A) = 0.30 х 0,02 + 0,15 х 0,04 + 0,2 х 0,05 = 0,022. Таким образом, если продукт не прошел проверку качества, вероятность того, что он был получен от машины A, составляет 19,67%, в отличие от в среднем 35% от общего объема производства. Что еще более интересно, несмотря на то, что производит только 35% всех продуктов, машина A на самом деле производит 54,3% всех продуктов, которые проходят проверку качества, что делает его намного более продуктивным, чем все остальные (при равных затратах и техобслуживании).
Как и в других примерах, достоверность вычислений зависит от действительности ввода .Если прошлое поведение машины по какой-то причине не позволяет предсказать будущее поведение машины, тогда вычисления с использованием теоремы Байеса могут быть произвольно отключены, например если машина A внезапно начинает производить продукцию со 100% дефектом из-за серьезной неисправности (в этом случае, если продукт не проходит проверку качества, у него есть колоссальные 96% шансов, что он будет произведен машиной A!).
Фильтрация спама
Допустим, у нас есть спам-фильтр, обученный с данными, в которых распространенность писем со словом «скидка» составляет 1%.Кроме того, он способен идентифицировать спам-сообщения с чувствительностью 98% (2% ложных отрицательных результатов) и 99,6% специфичностью (0,4% ложных положительных результатов). Если фильтру приходит электронное письмо, которое он определяет как спам, насколько вероятно, что оно содержит «скидку»? В этом случае, который эквивалентен случаю рака груди, очевидно, что все дело в базовой скорости, и что ни чувствительность, ни специфичность ничего об этом не говорят. Вероятность того, что идентифицированное электронное письмо содержит слово «скидка», может быть рассчитана с помощью калькулятора правила Байеса и равна всего 4.81%.
Возможно, более интересный вопрос заключается в том, сколько писем, которые не будут определены как спам, содержат слово «скидка». Ответ — всего 0,2%, что намного ниже, чем общая распространенность. Конечно, рассчитанная таким образом условная вероятность будет отключена, если тем временем спам изменится и наш фильтр фактически работает хуже, чем раньше, или если преобладание слова «скидка» изменилось и т. Д.
Ошибка базовой ставки
Случаи игнорирования базовой скорости или смещения базовой скорости являются классическими случаями, когда применение правила Байеса может помочь избежать ошибки.Заблуждение состоит в том, что, если ему представлена соответствующая базовая информация (общая информация) и конкретная информация (относящаяся только к рассматриваемому случаю, например, результат теста), разум имеет тенденцию игнорировать первое и сосредотачиваться на втором. Хорошо известный пример аналогичен приведенному выше примеру теста на наркотики: даже с тестом, который правильно определяет пьяных водителей в 100% случаев, если он также имеет ложноположительный показатель 5% для непьяных и процент нетрезвых водителей. -drunks очень мало (например, 1 из 999), тогда положительный результат теста во время случайной остановки означает, что есть только 1.96% вероятность, что человек действительно пьян.
Противоположность ошибки базовой ставки — это применить к неправильной базовой ставке или , чтобы полагать, что базовая ставка для определенной группы применима к рассматриваемому случаю, когда это не . В приведенном выше примере, хотя случайно выбранный человек из общей популяции водителей может иметь очень низкий шанс быть пьяным даже после положительного результата теста, если человек не был выбран случайным образом, например он демонстрировал неустойчивое вождение, неспособность придерживаться своей полосы движения, плюс они не прошли тест на координацию и пахли пивом, более неуместно применять базовую ставку 1 из 999, поскольку они больше не соответствуют критериям для случайно выбранного члена все население водителей.Скорее, они квалифицируются как «самые пьяные» …
Список литературы
[1] Байес Т. и Прайс Р. (1763) «Эссе по решению проблемы в Доктрине Шансов. Покойный преподобный г-н Байес, переданный г-ном Прайсом, в письме Джону Кантону, Массачусетс. и FRS », Philosophical Transactions of the Royal Society of London 53: 370–418
[2] Данные Программы США по надзору, эпидемиологии и конечным результатам (SEER).
[3] Якобсен, К.K. et al. (2015) «Сравнение чувствительности и специфичности скрининговой маммографии в США и Дании», International Journal of Cancer. Международный журнал Du Cancer 137 (9): 2198–2207; http://doi.org/10.1002/ijc.29593
Калькулятор возраста— Сколько мне лет?
Калькулятор возраста — сколько мне лет?Мой калькулятор возраста точно рассчитывает ваш точный возраст и дает ответ Сколько мне лет?
Выберите день рождения в день, месяц, год и, при желании, время вашего рождения в формате часов, минут и нажмите кнопку, чтобы узнать ответ для Сколько мне сегодня лет?
Также будет рассчитан ваш возраст как общее количество дней.
Возраст — это то, чем гордится один человек, а другой пытается скрыть это от всех. Традиционно возраст человека связан с его жизненным опытом, ценностями и мудростью. Известно, что наш возраст измеряется в хронологическом порядке, но не все знают, что в разных культурах возраст рассчитывается по-разному. То есть в некоторых странах возраст человека определяется со дня его рождения, а в некоторых считается, что новорожденному уже исполнился 1 год.В старомодной китайской культуре возраст человека рассчитывается по его традиционному Новому году, определяемому по традиционному китайскому лунному году.
Как пользоваться калькулятором моего возраста?
Вы хотите знать «Сколько вам лет?» , значит вы в нужном месте. Этот простой и легкий в использовании калькулятор возраста поможет вам рассчитать и узнать свой возраст традиционным европейским и американским способом на основе даты вашего рождения. Вычислите свой точный возраст более точно с помощью параметров часового пояса и времени рождения.Калькулятор возраста попытается определить ваш часовой пояс, и ваш возраст будет рассчитан в соответствии с выбранным часовым поясом (в нем должен быть установлен часовой пояс в месте вашего рождения). Все, что вам нужно сделать, это просто ввести дату вашего рождения в формате день, месяц, год, час, минута. В результате вы увидите свой возраст в годах, месяцах, днях, часах и минутах. Используя дату и время рождения, вы узнаете свой возраст сегодня и найдете ответ на вопрос : «Сколько мне лет прямо сейчас?» .
© 2020 www.MyAgeCalculator.com
Как вычислить лицо золотого сечения |
Написано: Бренда Скоттсдейл
Написано: 14 июля 2020 г.
Jupiterimages / Goodshoot / Getty Images
Насколько вы красивы, можно с научной точки зрения рассчитать с помощью золотого сечения. Золотое сечение проявляется в пропорциях многих естественных красивых вещей, будь то человек или водопад. Говорят, что у многих известных кинозвезд лица идеального золотого сечения.
Они привлекают вас, потому что их лица пропорциональны и ровны. Золотое сечение — 1,618. Вы можете сравнить любые две вещи, чтобы увидеть, соответствуют ли они золотому сечению, сложив их вместе и разделив большую часть. Если пропорция 1,618, она соответствует золотому сечению.
- Насколько вы красивы, можно научно подсчитать с помощью золотого сечения.
- Вы можете сравнить любые две вещи, чтобы увидеть, соответствуют ли они золотому сечению, сложив их вместе и разделив большую часть.
Medioimages / Photodisc / Valueline / Getty Images
Измерьте черты своего лица. Неважно, какие единицы измерения используются, если вы используете одну и ту же систему для всего. Измерьте ширину головы, носа, внешнего глаза до внешнего глаза и губ. Измерьте следующие расстояния: от макушки до подбородка, от макушки до зрачка, от зрачка до кончика носа, от зрачка до губы, от линии роста волос до зрачка, от кончика носа до Ваш подбородок, губы к подбородку и кончик носа к губам.
Вычислите следующие соотношения, разделив верхнюю часть (числитель) на нижнюю часть (знаменатель):
Верхняя часть головы до подбородка / ширина головы
Верхняя часть головы к вашему зрачку / ваш зрачок к вашему губа
- Измерьте черты лица.
- Вычислите следующие соотношения, разделив верхнюю часть (числитель) на нижнюю часть (знаменатель): верхняя часть головы до подбородка / ширина головы Верхняя часть головы до зрачка / от зрачка до губы
Кончик носа к подбородку / губы к подбородку
Кончик носа к подбородку / зрачок к кончику носа
Ширина носа / кончик носа до губ
Расстояние между за пределами глаз / от линии роста волос до зрачка
Длина губ / ширина носа.
Райан Маквей / Lifesize / Getty Images
Изучите полученные соотношения. Согласно золотому сечению, чем ближе каждое из этих соотношений к 1,618, тем красивее эта пропорция. Большинство лиц имеют некоторые пропорции, которые вполне соответствуют пропорциям, а другие могут быть далекими.
- Кончик носа к подбородку / губы к подбородку От кончика носа к подбородку / зрачок к кончику носа Ширина носа / кончик носа до губ Расстояние между краями глаз / линия роста волос до зрачка. Длина губ / ширина носа.

